Câu hỏi:
03/04/2024 58
Cho hàm số f(x)={x3+8x+mx−1 khi x≠1n khi x=1 , với m,n, là các tham số thực. Biết rằng hàm số f(x) liên tục tại x=1, khi đó hãy tính giá trị của biểu thức p= m+n ?
là các tham số thực. Biết rằng hàm số f(x) liên tục tại x=1, khi đó hãy tính giá trị của biểu thức p= m+n ?
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Tập xác định D=R.
Với x≠1 ta có f(x)=x3+8x+mx−1=x2+x+9+m+9x−1.
f(x) liên tục tại x=1 khi và chỉ khi limx→1f(x)=f(1)(1)
Nếu m+9≠0⇔m≠−9 thì không tồn tại limx→1f(x) vì limx→1+f(x)≠limx→1−f(x).
Do đó m+9=0⇔m=−9. Suy ra limx→1f(x)=limx→1(x2+x+9)=11.
Vậy (1)⇔n=11 suy ra P=m+n=−9+11=2.
Tập xác định D=R.
Với x≠1 ta có f(x)=x3+8x+mx−1=x2+x+9+m+9x−1.
f(x) liên tục tại x=1 khi và chỉ khi limx→1f(x)=f(1)(1)
Nếu m+9≠0⇔m≠−9 thì không tồn tại limx→1f(x) vì limx→1+f(x)≠limx→1−f(x).
Do đó m+9=0⇔m=−9. Suy ra limx→1f(x)=limx→1(x2+x+9)=11.
Vậy (1)⇔n=11 suy ra P=m+n=−9+11=2.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ba dãy số: (un) ; (vn) ; (wn) với un=12n; vn=(π3)n; wn=3n4n+1, với ∀n≥1. Trong ba dãy số đã cho, có bao nhiêu dãy số có giới hạn bằng 0?
Xem đáp án »
03/04/2024
135
Câu 3:
Cho hình lập phương ABCDA'B'C'D' , có cạnh a . Hãy tìm mệnh đề sai trong các mệnh đề sau:
Xem đáp án »
03/04/2024
85
Câu 7:
Cho tứ diện ABCD , gọi G là trọng tâm của tam giác BCD . Biết luôn tồn tại số thực k thỏa mãn đẳng thức vecto →AB+→AC+→AD=k.→AG. Hỏi số thực đó bằng bao nhiêu?
Xem đáp án »
03/04/2024
70
Câu 10:
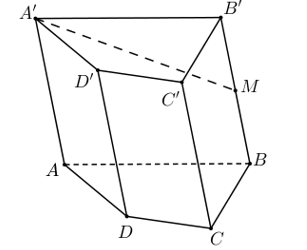
Cho hình lăng trụ tứ giác ABCD.A'. Gọi M là trung điểm của BB' Ảnh của đoạn thẳng A'M qua phép chiếu song song theo phương chiếu AA' lên mặt phẳng (ABCD) là đoạn thẳng
Xem đáp án »
03/04/2024
68


