Cho hàm số f(x)= ax^3+bx^2+cx+ d có đồ thị (C) Biết đồ thị (C) tiếp xúc

39 29/04/2024

Cho hàm số $f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị (C) Biết đồ thị (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ dương và đồ thị của hàm số $y = f^{'} (x)$ như hình vẽ:

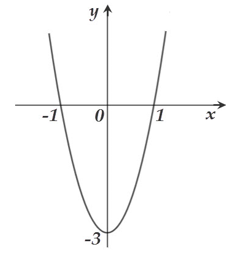
Cho hàm số f(x)= ax^3+bx^2+cx+ d có đồ thị (C) Biết đồ thị (C) tiếp xúc (ảnh 1)

Giá trị lớn nhất của hàm số $y = |f (x)|$ trên $[0; 2]$ bằng

A. 8.

B. 14.

C. 20.

D. 3.

Trả lời

Chọn A

Ta có $f' (x) = k (x - 1) (x + 1) = k (x^{2} - 1)$ . Lại có $f' (0) = - 3 \Rightarrow k = 3$ .

Do đó $f' (x) = 3 x^{2} - 3 \Rightarrow f (x) = x^{3} - 3 x + C$ .

phương trình sau có nghiệm x > 0: $\{\begin{cases} x^{3} - 3 x + C = 4 \\ 3 x^{2} - 3 = 0 \end{cases} \Leftrightarrow \{\begin{cases} C = 2 \\ x = - 1 (L o a i) \end{cases} \lor \{\begin{cases} C = 6 \\ x = 1 (N h a n) \end{cases}$ .

Suy ra $f (x) = x^{3} - 3 x + 6$ .

Xét trên $[0; 2]$ , ta có $f' (x) = 0 \Leftrightarrow x = 1$ . Mà $\{\begin{cases} f (0) = 6 \\ f (1) = 4 \\ f (2) = 8 \end{cases} \Rightarrow \max_{[0; 2]} f (x) = 8$ .

30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải

Xem tất cả

Cho hàm số f(x)= ax^3+bx^2+cx+ d có đồ thị (C) Biết đồ thị (C) tiếp xúc

Trả lời

Câu hỏi cùng chủ đề

Cho hình lăng trụ đứng ABC.A'B'C' có các cạnh AB=AA'=2a , đáy ABC là tam

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng

Cho các hàm số f(x) = mx^4+ mx^3+ px^2+ qx + r

Gọi S là tập hợp tất cả các số tự nhiên có 6 chữ số đôi một khác nhau và

Cho phương trình: 2^m .2 ^sin 2x + 3. 1/ 9 ^cos x +2 + m - cos(1)

Cho hàm số y= (x-1) ( x^2-2x-3) có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

Một bác nông dân có số tiền 20.000.000 đồng. Bác dùng số tiền đó gửi ngân hàng loại kì

Cho x,y là các số thực thỏa mãn (2x+ y) ^2.2^5x^2+2xy+2y^2-9 + ( x-y)^2=9

Cho hình chóp S.ABC có đáy là tam giác ABC có góc BAC= 120 độ, Bc=3a

Cho hàm số y= f(x) có đạo hàm trên ℝ và đồ thị hàm số y= f'(x) cắt trục hoành

Danh mục