Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.
Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.
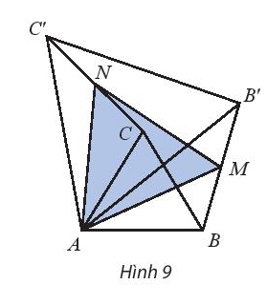
Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.

Do DABC là tam giác đều nên AB = AC và .
Do DAB’C’ là tam giác đều nên AB’ = AC’ và .
Ta có phép quay tâm A, góc quay 60° biến:
⦁ Điểm B thành điểm C;
⦁ Điểm B’ thành điểm C’.
Do đó ảnh của đoạn thẳng BB’ qua phép quay tâm A, góc quay 60° là đoạn thẳng CC’.
Mà M, N lần lượt là trung điểm của BB’, CC’ (giả thiết).
Do đó phép quay tâm A, góc quay 60° biến điểm M thành điểm N.
Suy ra AM = AN và .
DAMN có AM = AN và nên là tam giác đều.
Vậy ∆AMN đều.