Câu hỏi:
25/01/2024 65
Cho hai tam giác ABC và DEF thỏa mãn AB = DE, ,, AB = 5cm, AC = 6cm, EF = 8cm. Nửa chu vi p tam giác DEF nằm trong khoảng nào dưới đây:
Cho hai tam giác ABC và DEF thỏa mãn AB = DE, ,, AB = 5cm, AC = 6cm, EF = 8cm. Nửa chu vi p tam giác DEF nằm trong khoảng nào dưới đây:
A. 9 < p < 10;
A. 9 < p < 10;
B. 15 < p < 19;
B. 15 < p < 19;
C. 19 < p < 20;
D. 25 < p < 29.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Xét ∆ABC và ∆DEF, có:
(gt)
AB = DE (giả thiết)
(gt)
Do đó ∆ABC = ∆DEF (g.c.g)
⇒ AB = DE = 5cm, AC = DF = 6cm
Khi đó chu vi của tam giác DEF là: 5 + 6 + 8 = 19 cm.
Nửa chu vi của tam giác DEF là: 19 : 2 = 9,5 cm.
Vì vậy 9 < p < 10.
Vậy chọn đáp án A
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC. Gọi I là trung điểm của AC. Trên tia đối của tia IB, lấy điểm E sao cho IE = IB. Khẳng định nào sau đây đúng?
Cho ∆ABC. Gọi I là trung điểm của AC. Trên tia đối của tia IB, lấy điểm E sao cho IE = IB. Khẳng định nào sau đây đúng?
Câu 2:
Cho hình vẽ sau. Biết AB // CD và AD // BC.
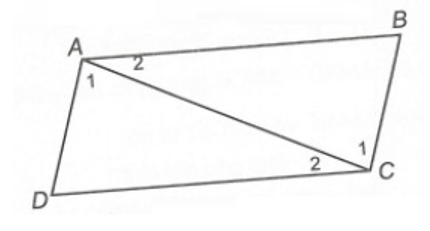
Hình vẽ trên có mấy cặp tam giác bằng nhau?
Câu 4:
Cho tam giác ABC cân tại A, có . Trên tia đối của tia BC lấy điểm D sao cho , trên tia đối của tia CB lấy điểm E sao cho BD = CE. Tính ?
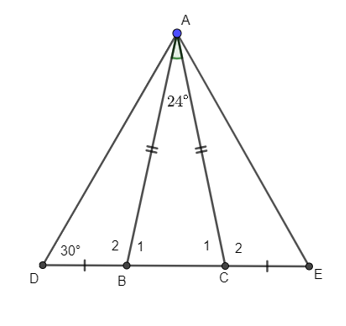
Cho tam giác ABC cân tại A, có . Trên tia đối của tia BC lấy điểm D sao cho , trên tia đối của tia CB lấy điểm E sao cho BD = CE. Tính ?

Câu 6:
Cho ∆ABC, điểm M thuộc cạnh BC. Đường thẳng đi qua M và song song với AB cắt AC ở D. Đường thẳng đi qua M và song song với AC cắt AB ở E.
Cho các khẳng định dưới đây:
(I) ;
(II) ME = AD;
(III) ∆AMD = ∆MAE.
Có bao nhiêu khẳng định đúng?
Cho ∆ABC, điểm M thuộc cạnh BC. Đường thẳng đi qua M và song song với AB cắt AC ở D. Đường thẳng đi qua M và song song với AC cắt AB ở E.
Cho các khẳng định dưới đây:
(I) ;
(II) ME = AD;
(III) ∆AMD = ∆MAE.
Có bao nhiêu khẳng định đúng?