Cho hai hình chữ nhật ABCD và A’B’C’D’ có A'B'/B'C' = AB/BC .Trên các tia AB, AC, AD

Bài 3 trang 89 Toán 8 Tập 2: Cho hai hình chữ nhật ABCD và A’B’C’D’ có $\frac{A^{\text{'}}{B}^{\text{'}}}{B^{\text{'}}{C}^{\text{'}}}=\frac{\mathrm{AB}}{\mathrm{BC}}.$  Trên các tia AB, AC, AD ta lần lượt lấy các điểm B’’, C’’, D’’sao cho $\frac{A{B^{\text{'}}}^{\text{'}}}{\mathrm{AB}}=\frac{A{C^{\text{'}}}^{\text{'}}}{\mathrm{AC}}=\frac{A{D^{\text{'}}}^{\text{'}}}{\mathrm{AD}}=\frac{B^{\text{'}}{C}^{\text{'}}}{\mathrm{BC}}.$  Chứng minh:

a) Hình chữ nhật AB’’C’’D’’ đồng dạng phối cảnh với hình chữ nhật ABCD;

b) AB’’ = A’B’, B’’C’’ = B’C’;

c) Hai hình chữ nhật ABCD và A’B’C’D’ là đồng dạng.

Trả lời

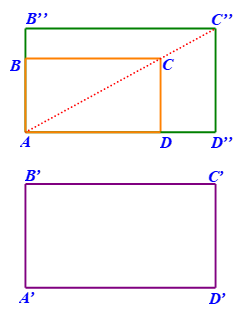
a) Ba đường thẳng AB’’, AC’’, AD’’ cùng đi qua điểm A và $\frac{A{B^{\text{'}}}^{\text{'}}}{\mathrm{AB}}=\frac{A{C^{\text{'}}}^{\text{'}}}{\mathrm{AC}}=\frac{A{D^{\text{'}}}^{\text{'}}}{\mathrm{AD}}$  nên hai hình chữ nhật A’’B’’C’’D’’ và ABCD là đồng dạng phối cảnh và điểm A là tâm đồng dạng phối cảnh.

b) Hai hình chữ nhật ABCD và A’B’C’D’ có $\frac{A^{\text{'}}{B}^{\text{'}}}{B^{\text{'}}{C}^{\text{'}}}=\frac{\mathrm{AB}}{\mathrm{BC}}$  nên $\frac{A^{\text{'}}{B}^{\text{'}}}{\mathrm{AB}}=\frac{B^{\text{'}}{C}^{\text{'}}}{\mathrm{BC}}.$

Mà $\frac{A{B^{\text{'}}}^{\text{'}}}{\mathrm{AB}}=\frac{A{C^{\text{'}}}^{\text{'}}}{\mathrm{AC}}=\frac{A{D^{\text{'}}}^{\text{'}}}{\mathrm{AD}}=\frac{B^{\text{'}}{C}^{\text{'}}}{\mathrm{BC}}$  (giả thiết) và $\frac{A{B^{\text{'}}}^{\text{'}}}{\mathrm{AB}}=\frac{{B^{\text{'}}}^{\text{'}}{C^{\text{'}}}^{\text{'}}}{\mathrm{BC}}$  (do A’’B’’C’’D’’ và ABCD là đồng dạng phối cảnh)

Suy ra $\frac{A{B^{\text{'}}}^{\text{'}}}{\mathrm{AB}}=\frac{{B^{\text{'}}}^{\text{'}}{C^{\text{'}}}^{\text{'}}}{\mathrm{BC}}=\frac{B^{\text{'}}{C}^{\text{'}}}{\mathrm{BC}}=\frac{A^{\text{'}}{B}^{\text{'}}}{\mathrm{AB}}$

Do đó AB’’ = A’B’, B’’C’’ = B’C’.

c) Hai hình chữ nhật A’’B’’C’’D’’ và A’B’C’D’ có: AB’’ = A’B’, B’’C’’ = B’C’ nên hai hình chữ nhật A’B’C’D’ và A’’B’’C’’D’’ bằng nhau.

Mà hình chữ nhật A’’B’’C’’D’’ đồng dạng phối cảnh với hình chữ nhật ABCD.

Vậy hai hình chữ nhật ABCD và A’B’C’D’ là đồng dạng.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Bài 9: Hình đồng dạng

Bài 10: Hình đồng dạng trong thực tiễn

Bài tập cuối chương 8

Chủ đề 3: Thực hành đo chiều cao