Lời giải
a)
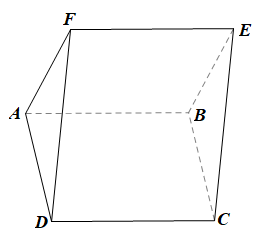
Ta có: BE // AF (do ABEF là hình bình hành);
AF ⊂ (AFD)
Do đó BE // (AFD).
Ta cũng có: BC // AD (do ABCD là hình bình hành)
AD ⊂ (AFD)
Do đó BC // (AFD).
Do BE // (AFD);
BC // (AFD);
BE, BC cắt nhau tại điểm B và cùng nằm trong mp(BEC)
Suy ra (AFD) // (BEC).
b)
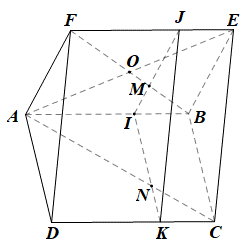
+) Do (AFD) song song với (P) nên tồn tại hai đường thẳng trong (AFD) song song với (P).
• Trong mp(ABEF), qua điểm M vẽ đường thẳng song song với AF, đường thẳng này cắt AB, EF lần lượt tại I, J.
Khi đó IJ // AF, mà AF ⊂ (AFD) nên IJ // (AFD).
• Trong mp(ABCD), qua điểm I vẽ đường thẳng song song với AD, cắt CD tại K.
Khi đó IK // AD, mà AD ⊂ (AFD) nên IK // (AFD).
• Ta có: IJ // (AFD);
IK // (AFD);
IJ, IK cắt nhau tại điểm I và cùng nằm trong mp(IJK).
Do đó (IJK) // (AFD).
Mà M ∈ IJ, IJ ⊂ (IJK) nên mp (P) đi qua M và song song với (AFD) chính là mp(IJK).
+) Trong mp(ABCD), AC cắt IK tại N, khi đó N là giao điểm của AC và (P).
Trong mp(ABCD), xét DABC có IN // BC (do IK // AD // BC) nên theo định lí Thalès ta có: ANNC=AIIB.
Trong mp(ABEF), xét DABF có IM // AF nên theo định lí Thalès ta có: AIIB=FMMB.
Gọi O là tâm hình bình hành ABEF. Khi đó O là trung điểm của FB nên FO = OB.
Do M là trọng tâm của DABE nên MB=23OB và OM=13OB.
Ta có: ANNC=AIIB=FMMB=FO+OMMB=OB+13OB23OB=43OB23OB=2.
Vậy AMNC=2.


