Câu hỏi:
31/01/2024 59
Cho , Ot là tia phân giác của và H là một điểm bất kì thuộc tia Ot. Qua H, lần lượt vẽ đường thẳng vuông góc với Ox tại A, cắt Oy tại C và đường thằng vuông góc với Oy tại B, cắt Ox tại D. Hỏi OH là đường trung trực của đoạn thẳng:
Cho , Ot là tia phân giác của và H là một điểm bất kì thuộc tia Ot. Qua H, lần lượt vẽ đường thẳng vuông góc với Ox tại A, cắt Oy tại C và đường thằng vuông góc với Oy tại B, cắt Ox tại D. Hỏi OH là đường trung trực của đoạn thẳng:
A. BD;
A. BD;
B. AB;
C. CD;
D. Đáp án B, C đúng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
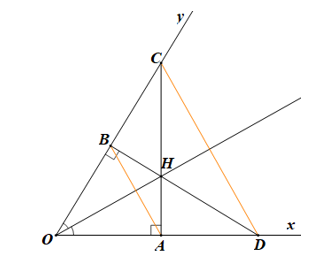
Xét ∆HAO và ∆HBO, có:
.
(do OH là phân giác của ).
OH là cạnh chung.
Do đó ∆HAO = ∆HBO (cạnh huyền – góc nhọn).
Suy ra HA = HB và OA = OB (các cặp cạnh tương ứng).
Do đó H và O nằm trên đường trung trực của AB
Khi đó OH là đường trung trực của đoạn thẳng AB.
Do đó đáp án B đúng.
Xét ∆OAC và ∆OBD, có:
.
OA = OB (chứng minh trên).
là góc chung.
Do đó ∆OAC = ∆OBD (cạnh góc vuông – góc nhọn kề).
Suy ra OC = OD (cặp cạnh tương ứng).
Do đó O nằm trên đường trung trực của CD (1)
Xét ∆HBC và ∆HAD, có:
(hai góc đối đỉnh).
HA = HB (chứng minh trên).
.
Do đó ∆HBC = ∆HAD (cạnh góc vuông – góc nhọn kề).
Suy ra HC = HD (cặp cạnh tương ứng).
Do đó H nằm trên đường trung trực của CD (2)
Từ (1) và (2) suy ra OH là đường trung trực của đoạn thẳng CD.
Do đó đáp án C đúng.
Ta có BD không vuông góc với AB.
Mà OH là đường trung trực của đoạn thẳng AB.
Nên OH không thể là đường trung trực của đoạn thẳng BD.
Do đó đáp án A sai.
Vậy ta chọn đáp án D.
Đáp án đúng là: D
Xét ∆HAO và ∆HBO, có:
.
(do OH là phân giác của ).
OH là cạnh chung.
Do đó ∆HAO = ∆HBO (cạnh huyền – góc nhọn).
Suy ra HA = HB và OA = OB (các cặp cạnh tương ứng).
Do đó H và O nằm trên đường trung trực của AB
Khi đó OH là đường trung trực của đoạn thẳng AB.
Do đó đáp án B đúng.
Xét ∆OAC và ∆OBD, có:
.
OA = OB (chứng minh trên).
là góc chung.
Do đó ∆OAC = ∆OBD (cạnh góc vuông – góc nhọn kề).
Suy ra OC = OD (cặp cạnh tương ứng).
Do đó O nằm trên đường trung trực của CD (1)
Xét ∆HBC và ∆HAD, có:
(hai góc đối đỉnh).
HA = HB (chứng minh trên).
.
Do đó ∆HBC = ∆HAD (cạnh góc vuông – góc nhọn kề).
Suy ra HC = HD (cặp cạnh tương ứng).
Do đó H nằm trên đường trung trực của CD (2)
Từ (1) và (2) suy ra OH là đường trung trực của đoạn thẳng CD.
Do đó đáp án C đúng.
Ta có BD không vuông góc với AB.
Mà OH là đường trung trực của đoạn thẳng AB.
Nên OH không thể là đường trung trực của đoạn thẳng BD.
Do đó đáp án A sai.
Vậy ta chọn đáp án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hai nhà máy được xây dựng tại hai địa điểm A và B cùng nằm về một phía của khúc sông thẳng. Lấy điểm mốc D ở phía bên kia bờ sông là điểm đối xứng của nhà máy A qua khúc sông thẳng.
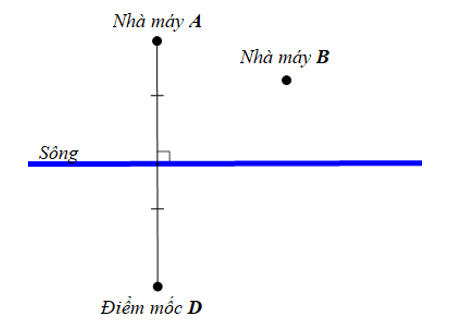
Tìm trên bờ sông một địa điểm C để xây dựng trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ C đến A và đến B nhỏ nhất.
Hai nhà máy được xây dựng tại hai địa điểm A và B cùng nằm về một phía của khúc sông thẳng. Lấy điểm mốc D ở phía bên kia bờ sông là điểm đối xứng của nhà máy A qua khúc sông thẳng.
Tìm trên bờ sông một địa điểm C để xây dựng trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ C đến A và đến B nhỏ nhất.
Câu 2:
Cho ∆ABC cố định, đường phân giác AI (I ∈ BC). Trên đoạn thẳng IC lấy điểm H. Từ H kẻ đường thẳng song song với AI, cắt AB kéo dài tại E và cắt AC tại F. Chọn khẳng định đúng.
Cho ∆ABC cố định, đường phân giác AI (I ∈ BC). Trên đoạn thẳng IC lấy điểm H. Từ H kẻ đường thẳng song song với AI, cắt AB kéo dài tại E và cắt AC tại F. Chọn khẳng định đúng.
Câu 3:
Cho đoạn thẳng AB = 5 cm. Vẽ đường tròn tâm A, bán kính 4 cm và đường tròn tâm B, bán kính 3 cm. Hai đường tròn này cắt nhau tại D và E. Khẳng định nào sau đây đúng nhất?
Cho đoạn thẳng AB = 5 cm. Vẽ đường tròn tâm A, bán kính 4 cm và đường tròn tâm B, bán kính 3 cm. Hai đường tròn này cắt nhau tại D và E. Khẳng định nào sau đây đúng nhất?
Câu 4:
Cho ∆MNP vuông tại M có . Trên tia đối của tia MP, lấy điểm Q sao cho MQ = MP. Tính số đo .
Cho ∆MNP vuông tại M có . Trên tia đối của tia MP, lấy điểm Q sao cho MQ = MP. Tính số đo .
Câu 5:
Cho ∆DEF cân tại D. Lấy điểm K nằm trong ∆DEF sao cho KE = KF. Kẻ KP vuông góc với DE (P ∈ DE), KQ vuông góc DF (Q ∈ DF). Điểm K thuộc đường trung trực của đoạn thẳng:
Cho ∆DEF cân tại D. Lấy điểm K nằm trong ∆DEF sao cho KE = KF. Kẻ KP vuông góc với DE (P ∈ DE), KQ vuông góc DF (Q ∈ DF). Điểm K thuộc đường trung trực của đoạn thẳng:
Câu 6:
Cho . Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B. Lấy điểm C sao cho OB là đường trung trực của AC. Chọn khẳng định sai.
Câu 7:
Cho đoạn thẳng AB. Dựng các tam giác PAB cân tại P và tam giác QAB cân tại Q như hình bên.
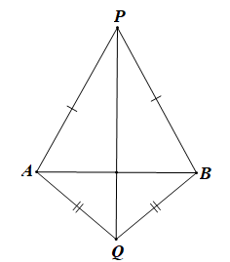
Chọn khẳng định đúng nhất.
Cho đoạn thẳng AB. Dựng các tam giác PAB cân tại P và tam giác QAB cân tại Q như hình bên.
Chọn khẳng định đúng nhất.
Câu 8:
Cho đường thẳng d cắt đoạn thẳng AB tại một điểm khác trung điểm của AB. Xác định vị trí điểm M trên đường thẳng d sao cho M cách đều hai điểm A, B.
Cho đường thẳng d cắt đoạn thẳng AB tại một điểm khác trung điểm của AB. Xác định vị trí điểm M trên đường thẳng d sao cho M cách đều hai điểm A, B.
Câu 9:
Cho ∆ABC nhọn có AB < AC. Xác định điểm D trên cạnh AC sao cho DA + DB = AC.
Cho ∆ABC nhọn có AB < AC. Xác định điểm D trên cạnh AC sao cho DA + DB = AC.
Câu 10:
Một con đường quốc lộ có vị trí với hai điểm dân cư A và B như hình vẽ dưới đây.
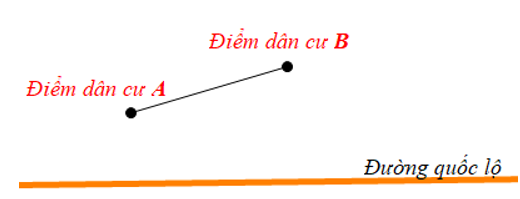
Hãy tìm trên đường quốc lộ đó một địa điểm C để xây dựng trạm y tế sao cho trạm y tế cách đều hai điểm dân cư A và B.
Một con đường quốc lộ có vị trí với hai điểm dân cư A và B như hình vẽ dưới đây.
Hãy tìm trên đường quốc lộ đó một địa điểm C để xây dựng trạm y tế sao cho trạm y tế cách đều hai điểm dân cư A và B.
Câu 11:
Cho . Trên các tia Ox, Oy lần lượt lấy hai điểm A, B (không trùng với O). Đường trung trực của các đoạn thẳng OA và OB cắt nhau tại H. Khẳng định nào sau đây đúng nhất?
Cho . Trên các tia Ox, Oy lần lượt lấy hai điểm A, B (không trùng với O). Đường trung trực của các đoạn thẳng OA và OB cắt nhau tại H. Khẳng định nào sau đây đúng nhất?
Câu 13:
Cho hai điểm A, B nằm trên đường trung trực của đoạn thẳng CD. Gọi M là trung điểm CD. Khẳng định nào sau đây đúng nhất?
Câu 14:
Cho ∆ABC vuông tại A có . Trên tia đối của tia AC lấy điểm D sao cho AC = AD. ∆BCD là tam giác gì?
Cho ∆ABC vuông tại A có . Trên tia đối của tia AC lấy điểm D sao cho AC = AD. ∆BCD là tam giác gì?


