Câu hỏi:
29/01/2024 101Cho ^mOn và ^nOp là hai góc kề bù. Biết ^mOn=110∘ và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
A. 145°;
B. 135°;
C. 45°;
D. 35°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
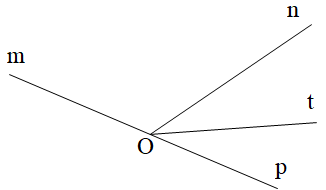
Vì ^mOn và ^nOp là hai góc kề bù nên ^mOn+^nOp=180∘
Suy ra ^nOp=180∘−^mOn
Hay ^nOp=180∘−110∘=70∘
Mà ^nOt=^tOp=^nOp2 (vì Ot là tia phân giác góc nOp)
Suy ra ^nOt=^tOp=^nOp2=70∘2=35∘
Vì hai góc mOn và nOp là hai góc kề bù nên tia On nằm giữa hai tia Om và Op; tia Ot là phân giác của góc nOp nên tia Ot nằm giữa hai tia On và Op.
Do đó tia Ot nằm giữa hai tia On nằm giữa hai tia Om và Ot
Suy ra ^mOt=^mOn+^nOt suy ra ^mOt=110∘+35∘=145∘
Vậy ^mOt=145∘.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Cho định lí: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông”. Giả thiết, kết luận của định lí là:
Câu 5:
Cho ^xOy=120∘, tia Ot là tia phân giác của góc xOy. Tính số đo góc xOt
Câu 6:
Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
Hình vẽ minh hoạ cho định lí trên là:
Câu 10:
Hai đường thẳng xy và x’y’ cắt nhau tại O. Góc đối đỉnh của ^xOy′ là:
Câu 11:
Cho hình chữ nhật ABCD như hình vẽ. Biết IJ // AB và ^JOC=30∘.
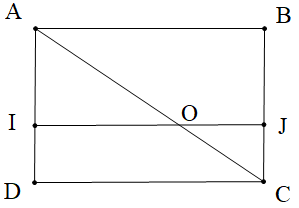
Số đo góc BAC là:
Câu 14:
Cho góc AOB và OI tia phân giác của góc đó. Vẽ tia phân giác OJ của góc BOI. Biết ^IOJ=25∘. Số đo góc AOB là: