Cho đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b trong mặt phẳng (P). Xét một đường thẳng c bất kì trong (P) (c không song song với a và b). Gọi O là giao điểm của d và (P). Trong (P) vẽ qua O ba đường thẳng lần lượt song song với a, b, c. Vẽ một đường thẳng cắt a′, b′, c′ lần lượt tại B, C, D. Trên d lấy hai điểm E, F sao cho O là trung điểm của EF (Hình 4).

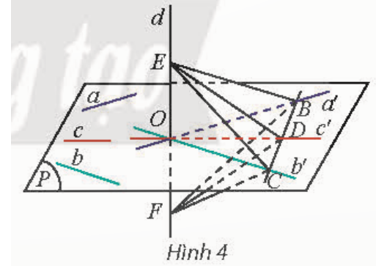
a) Giải thích tại sao hai tam giác CEB và CFE bằng nhau.

a) Ta có: $\left.\begin{array}{l}d\perp a\\ a\text{'}\perp a\end{array}\right\}\Rightarrow d\perp a\text{'}\Rightarrow \text{EF}\perp O\text{B}$

Tam giác EBF có EF ⊥ OB

O là trung điểm của EF

 $\Rightarrow$Tam giác EBF cân tại B.

$\Rightarrow$ BE = BF

Tương tự: $\left.\begin{array}{l}d\perp b\\ b\text{'}\perp b\end{array}\right\}\Rightarrow d\perp b\text{'}\Rightarrow \text{EF}\perp OC$

Tam giác ECF có EF ⊥ OC

O là trung điểm của EF

$\Rightarrow$ Tam giác ECF cân tại C .

$\Rightarrow$ CE = CF

Xét ΔCEB và ΔCFB có:

BE = BF; CE = CF; cạnh BC chung

Do đó ΔCEB = ΔCFB (c.c.c)