Bài 4 trang 15 Toán lớp 10 Tập 1: Cho các định lí
P: “ Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”
Q: “Nếu a < b thì a + c < b + c” (a, b, c ℝ).
a) Chỉ ra giả thiết và kết luận của mỗi định lí;
b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”.
c) Mệnh đề đảo của mỗi định lí đó có là định lí không?
a)
Giả thiết của định lí P: hai tam giác bằng nhau.
Kết luận của định lí P: diện tích của chúng bằng nhau.
Giả thiết của định lí Q: a < b
Kết luận của định lí Q: a + c < b + c
b)
Sử dụng thuật ngữ “điều kiện cần”:
Định lí P: Để hai tam giác bằng nhau điều kiện cần là chúng có diện tích bằng nhau.
Định lí Q: Để a < b điều kiện cần là a + c < b + c, (a, b, c ℝ).
Sử dụng thuật ngữ “điều kiện đủ”:
Định lí P: “Để hai tam giác có diện thích bằng nhau điều kiện đủ là hai tam giác bằng nhau”.
Định lí Q: Để a + c < b + c điều kiện đủ là a < b, (a, b, c ℝ).
c)
Mệnh đề đảo của mệnh đề P: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác bằng nhau”.
Mệnh đề đảo của mệnh đề P không phải là định lí vì
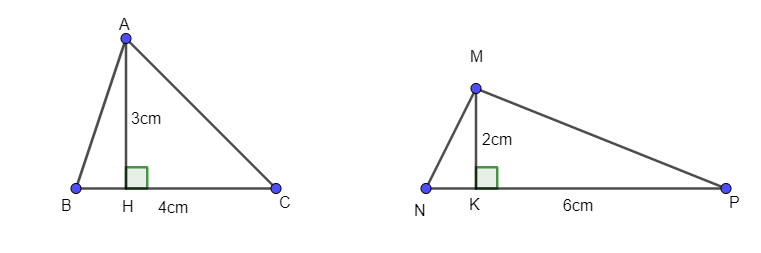
Hai tam giác ABC và MNP có cùng diện tích là 12 cm2. Tuy nhiên hai tam giác này không bằng nhau. Do đó mệnh đề đảo của P là sai nên mệnh đề đảo của P không phải là định lí.
Mệnh đề đảo của mệnh đề Q: Nếu a + c < b + c thì a < b, (a, b, c ℝ).
Mệnh đề đảo của mệnh đề Q là định lí, vì mệnh đề đảo của mệnh đề Q là mệnh đề đúng. Theo tính chất của bất phương trình nếu cộng vào 2 vế của bất phương trình cùng một số thì bất phương trình không thay đổi.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Các phép toán trên tập hợp