Các phép biến hình sau có phải là phép vị tự không: phép đối xứng tâm, phép đối xứng trục, phép đồng nhất, phép tịnh tiến theo vectơ khác $\overrightarrow{0}$?

⦁ Phép đối xứng tâm là phép vị tự tâm O, tỉ số k = –1.

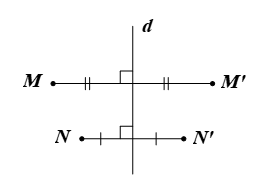
⦁ Xét phép đối xứng trục:

Giả sử ta chọn đường thẳng d bất kì.

Với mỗi điểm M ∉ d, ta có M’ là ảnh của M qua phép đối xứng trục d.

Do đó d là đường trung trực của MM’.

Suy ra d ⊥ MM’   (1)

Với mỗi điểm N ∉ d và N ≠ M, ta cũng có N’ là ảnh của N qua phép đối xứng trục d.

Do đó d là đường trung trực của NN’.

Suy ra d ⊥ NN’    (2)

Từ (1), (2), ta suy ra MM’ // NN’ hay MM’ và NN’ không có điểm chung.

Do đó phép đối xứng trục không phải là phép vị tự.

⦁ Phép đồng nhất là phép vị tự tâm I, tỉ số k = 1, với I là một điểm bất kì.

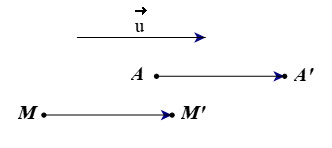
⦁ Xét phép tịnh tiến:

Giả sử ta chọn $\overrightarrow{u}\ne \overrightarrow{0}$.

Ta có phép tịnh tiến theo $\overrightarrow{u}\ne \overrightarrow{0}$ biến điểm A thành điểm A’.

Tức là, $\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{u}$.

Tương tự như vậy, với mỗi điểm M bất kì và điểm M’ là ảnh của M qua phép tịnh tiến theo $\overrightarrow{u}\ne \overrightarrow{0}$, ta đều có $\overrightarrow{M{M}^{\text{'}}}=\overrightarrow{u}$.

Ta thấy tồn tại ít nhất một cặp $\overrightarrow{A{A}^{\text{'}}},\overrightarrow{M{M}^{\text{'}}}$ không có điểm chung.

Tức là, tồn tại ít nhất một cặp đường thẳng AA’ và MM’ song song với nhau.

Do đó phép tịnh tiến không phải là phép vị tự.

Vậy phép đối xứng tâm và phép đồng nhất là phép vị tự; phép đối xứng trục và phép tịnh tiến không phải là phép vị tự.