Gieo liên tiếp một con xúc xắc cân đối và một đồng xu cân đối. Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu
545
11/04/2023
Bài 9.9 trang 86 Toán 10 Tập 2: Gieo liên tiếp một con xúc xắc cân đối và một đồng xu cân đối.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của các biến cố sau:
F: “Đồng xu xuất hiện mặt ngửa”;
G: “Đồng xu xuất hiện mặt sấp hoặc số chấm xuất hiện trên con xúc xắc là 5”.
Trả lời
a) Đồng xu và con xúc xắc cân đối nên các kết quả xảy ra có thể đồng khả năng.
Gieo một con xúc xắc, các kết quả có thể xảy ra là 1, 2, 3, 4, 5, 6 chấm.
Gieo một đồng xu, các kết quả có thể xảy ra là xuất hiện mặt sấp hoặc mặt ngửa.
Kí hiệu S là mặt sấp, N là mặt ngửa.
Sơ đồ hình cây mô tả các phần tử của không gian mẫu là:
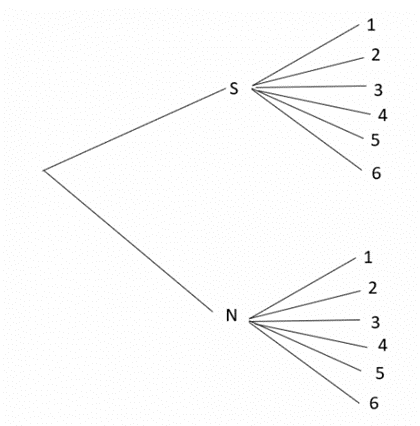
Các kết quả có thể là: S1; S2; S3; S4; S5; S6; N1; N2; N3; N4; N5; N6.
Do đó, Ω = {S1; S2; S3; S4; S5; S6; N1; N2; N3; N4; N5; N6}.
Vậy n(Ω) = 12.
b)
+ Biến cố F: “Đồng xu xuất hiện mặt ngửa”.
Các kết quả thuận lợi cho biến cố F là: N1; N2; N3; N4; N5; N6.
Do đó, F = {N1; N2; N3; N4; N5; N6}.
⇒ n(F) = 6.
Vậy P(F)=n(F)n(Ω)=612=12.
+ Biến cố G: “Đồng xu xuất hiện mặt sấp hoặc số chấm xuất hiện trên con xúc xắc là 5”.
Các kết quả thuận lợi cho biến cố G là: S1; S2; S3; S4; S5; S6; N5.
Do đó, G = {S1; S2; S3; S4; S5; S6; N5}.
⇒ n(G) = 7.
Vậy P(G)=n(G)n(Ω)=712.

