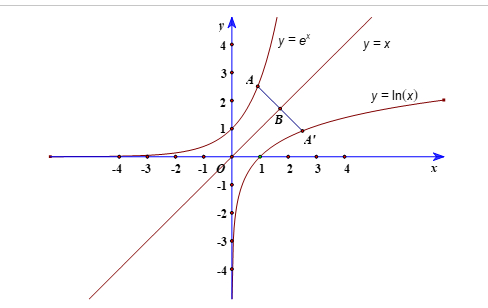
b) Chứng minh rằng hai đồ thị trên đối xứng nhau qua đường thẳng y = x, tức là nếu điểm M nằm trên một đồ thị thì điểm M’ đối xứng với M qua đường thẳng y = x sẽ nằm trên đồ thị còn lại.
36
16/10/2024
b) Chứng minh rằng hai đồ thị trên đối xứng nhau qua đường thẳng y = x, tức là nếu điểm M nằm trên một đồ thị thì điểm M’ đối xứng với M qua đường thẳng y = x sẽ nằm trên đồ thị còn lại.
Trả lời
b) Xét điểm A(x0;ex0) nằm trên đồ thị hàm số y = ex.
Phương trình đường thẳng (d) đi qua điểm A(x0;ex0) và vuông góc với đường thẳng y = x có dạng :y=−x+x0+ex0 .
Gọi B là giao điểm của đường thẳng (d) và đường thẳng y = x.
Khi đó B(x0+ex02;x0+ex02) .
Gọi A’ là điểm đối xứng với A qua đường thẳng y = x. Khi đó B là trung điểm của AA’.
Do đó {xA' . Vậy .
Thay tọa độ điểm vào hàm số y = ln x, ta được (luôn đúng),
Vậy thuộc đồ thị hàm số y = ln x.
Tương tự, nếu B(x0; ln x0) nằm trên đồ thị hàm số y = ln x thì ta cũng tìm được điểm B’ đối xứng với B qua đường thẳng y = x và điểm B’ thuộc đồ thị hàm số y = ex.
Vậy hai đồ thị đã cho đối xứng với nhau qua đường thẳng y = x.