a) Cho P là một điểm bên trong tam giác ABC. Chứng minh rằng: AB + AC > PB + PC.

Bài 9.13 trang 52 SBT Toán 7 Tập 2:

a) Cho P là một điểm bên trong tam giác ABC. Chứng minh rằng:

AB + AC > PB + PC.

b) Cho M là một điểm bên trong tam giác ABC. Chứng minh rằng:

$\frac{1}{2}\left(AB+BC+CA\right)<MA+MB+MC<AB+BC+CA$

Trả lời

a)

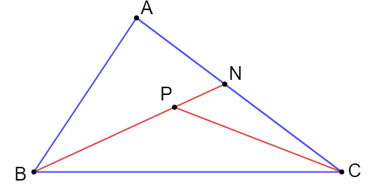
Lấy N là giao điểm của đường thẳng AC và BP.

Ta có: AB + AC = AB + (AN + NC) = (AB + AN) + NC (1)

Áp dụng bất đẳng thức tam giác vào tam giác ABN nên suy ra: AB + AN > BN (2)

Từ (1) và (2) suy ra:

AB + AC > BN + NC = (BP + NP) + NC

= PB + (NP + NC) (3)

Áp dụng bất đẳng thức tam giác vào tam giác CPN nên suy ra:

NP + NC > PC (4)

Từ (3) và (4) suy ra: AB + AC > PB + PC (đpcm).

b)

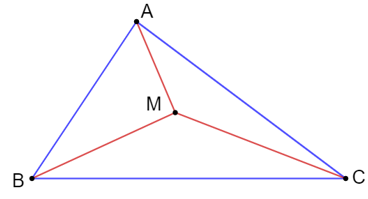
Áp dụng bất đẳng thức tam giác vào tam giác MAB ta có:

MA + MB > AB (5)

Tương tự với các tam giác MBC và MAC ta lần lượt suy ra được:

MB + MC > BC và MA + MC > AC (6).

Từ (5) và (6) ta suy ra được:

(MA + MB) + (MB + MC) + (MA + MC) > AB + BC + AC

Hay 2(MA + MB + MC) > AB + BC + AC

Suy ra $\frac{1}{2}\left(AB+BC+CA\right)<MA+MB+MC(\ast )$

Mặt khác chứng minh tương tự theo a) ta có:

AB + AC > MB + MC; AC + BC > MA + MB; BC + BA > MC + MA.

Từ đó ta suy ra được:

(MA + MB) + (MB + MC) + (MA + MC) < (AC + AB) + (AB + AC) + (BC + BA)

Hay 2(MA + MB + MC) < 2(AB + BC + CA)

Suy ra MA + MB + MC < AB + BC + CA (**)

Từ (*) và (**) ta suy ra:

$\frac{1}{2}\left(AB+BC+CA\right)<MA+MB+MC<AB+BC+CA$ (đpcm).