a) Biểu diễn miền nghiệm của hệ bất phương trình (I)

Bài 27 trang 32 SBT Toán 10 Tập 1: a) Biểu diễn miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}3x-y\le 9\\ 3x+6y\le 30\\ x\ge 0\\ 0\le y\le 4\end{array}\right.$(I).

b) Tìm x, y là nghiệm của hệ bất phương trình (I) sao cho F = 3x + 4y đạt giá trị lớn nhất.

Trả lời

Vẽ các đường thẳng:

d₁: 3x – y = 9 là đường thẳng đi qua hai điểm có tọa độ là (3; 0) và (0; 9).

d₂: 3x + 6y = 30 là đường thẳng đi qua hai điểm (10; 0) và (0; 5).

d₃: x = 0 là trục tung.

d₄: y = 0 là trục hoành

d₅: y = 4 là đường thẳng đi qua điểm (0; 4) và song song với trục hoành.

Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình trong hệ ta được miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình dưới đây chính là miền ngũ giác OABCD với O(0; 0), A(0; 4), B(2; 4), C(4; 3), D(3; 0):

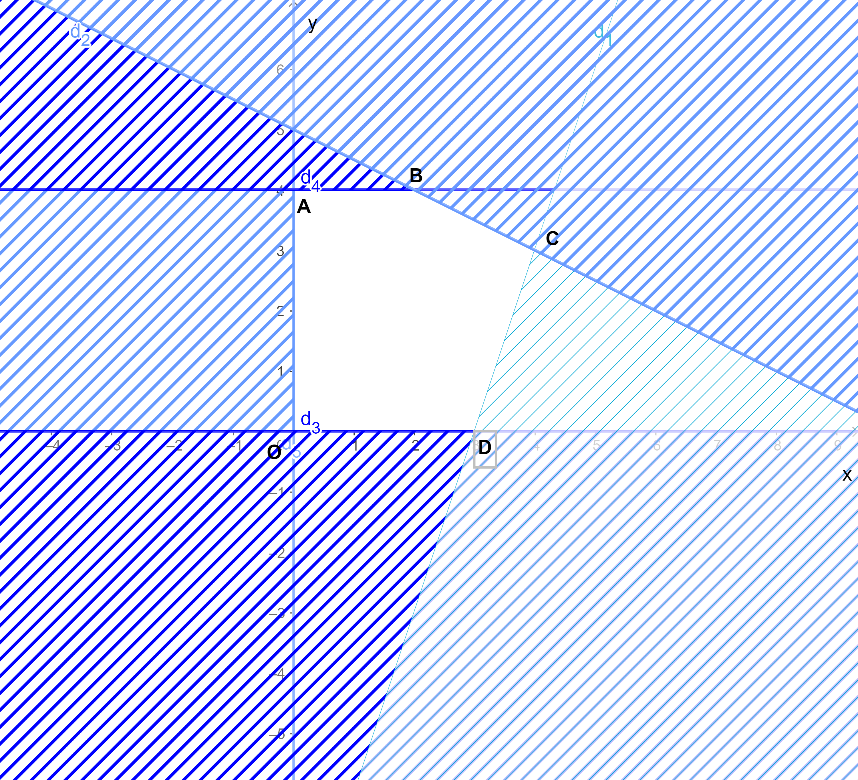
b) Biểu thức F = 3x + 4y đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác OABCD.

Tính giá trị biểu thức F tại các điểm, ta được:

Tại O(0; 0) với x = 0 và y = 0 thì F = 3.0 + 4.0 = 0;

Tại A(0; 4) với x = 0 và y = 4 thì F = 3.0 + 4.4 = 16;

Tại B(2; 4) với x = 2 và y = 4 thì F = 3.2 + 4.4 = 22;

Tại C(4; 3) với x = 4 và y = 3 thì F = 3.4 + 4.3 = 24;

Tại D(3; 0) với x = 3 và y = 0 thì F = 3.3 + 4.0 = 9.

Từ đó giá trị lớn nhất của F là 24 với x = 4 và y = 3.

Vậy giá trị lớn nhất của F bằng 24 khi x = 4 và y = 3.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài ôn tập chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai