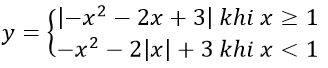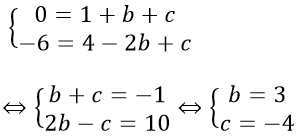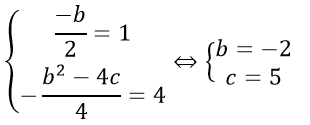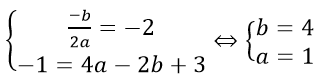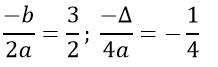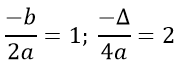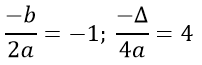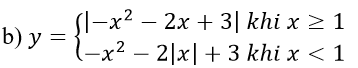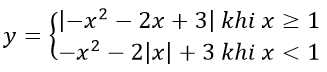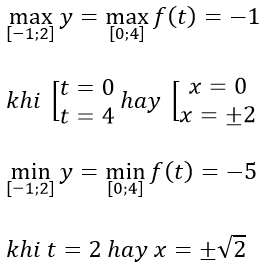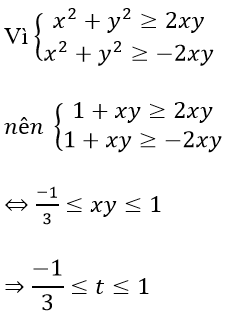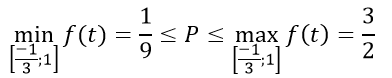Cách vẽ đồ thị hàm số bậc 2 chi tiết nhất và bài tập (2024)

CÁCH VẼ ĐỒ THỊ HÀM SỐ BẬC 2

1. Cách vẽ đồ thị hàm số bậc 2: y = ax²+ bx + c (a ≠ 0)

Đồ thị của hàm số bậc hai y = ax² + bx + c (a ≠ 0) là một đường parabol có đỉnh I có tọa độ là  và đồ thị này có một trục đối xứng, đó là đường thẳng . Đồ thị này có bề lõm hướng lên trên nếu a > 0 và hướng xuống dưới nếu a < 0.

Dưới đây là các bước vẽ đồ thị hàm số bậc 2 dạng y = ax² + bx + c (a ≠ 0):

• Bước 1. Ta xác định tọa độ của đỉnh I, đó là: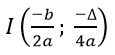

• Bước 2. Ta vẽ trục đối xứng của đồ thị là đường thẳng x = (-b)/(2a)

• Bước 3. Ta xác định các tọa độ là các giao điểm của parabol với trục hoành và trục tung của hệ trục tọa độ (nếu có). Tiếp tục xác định thêm một số điểm khác cũng thuộc đồ thị, ví dụ điểm đối xứng với giao điểm của đồ thị với trục tung để khi ta vẽ đồ thị được chuẩn hơn

• Bước 4. Thực hiện vẽ parapol (P). Ta cần chú ý đến dấu của hệ số a của hàm số khi bắt đầu vẽ đồ thị như sau:

+ Nếu a > 0 thì bề lõm của đồ thị hướng lên trên

+ Nếu a < 0 thì bề lõm của đồ thị hướng xuống dưới.

Ví dụ 1. Hãy vẽ đồ thị của hàm số bậc hai y = x² + 2x – 3.

Lời giải

Đồ thị của hàm số bậc hai y = x² + 2x – 3 có:

+ Đỉnh I (– 1 ; – 4);

+ Trục đối xứng x = – 1.

Giao điểm của đồ thị với trục tung là điểm A (0 ; – 3).

Điểm đối xứng với điểm A (0 ; – 3) qua trục đối xứng x = – 1 là điểm D (– 2 ; – 3).

Giao điểm của đồ thị với trục hoành là điểm B (– 3 ; 0) và điểm C (1 ; 0).

Vì a = 1 > 0, do đó đồ thị của hàm số bậc hai y = x² + 2x – 3 có bề lõm hướng lên.

Ta vẽ đồ thị của hàm số bậc hai y = x² + 2x – 3 như sau:

2. Cách vẽ đồ thị hàm số bậc 2: y = |ax²+ bx + c| (a ≠ 0)

Dưới đây là các bước vẽ đồ thị hàm số bậc 2 dạng y = |ax² + bx + c| (a ≠ 0):

• Bước 1. Ta thực hiện vẽ đồ thị hàm số bậc hai y = ax² + bx + c (P1) như ở mục 1

• Bước 2. Ta vẽ đồ thị hàm số bậc hai y = – (ax² + bx + c) (P2) bằng cách lấy phần đối xứng với (P1) qua trục hoành

• Bước 3. Ta xóa đi các phần của (P1) và (P2) nằm ở phía dưới của trục hoành Ox.

3. Cách vẽ đồ thị hàm số bậc 2: y = ax²+ b|x| + c (a ≠ 0)

Dưới đây là các bước vẽ đồ thị hàm số bậc 2 dạng y = ax² + b|x| + c (a ≠ 0):

• Bước 1.Ta thực hiện vẽ đồ thị hàm số bậc hai y = ax² + bx + c (P1) như ở mục 1

• Bước 2. Ta giữ nguyên phần bên phải của (P1) qua trục tung và xóa đi phần bên trái của (P1) qua trục tung

• Bước 3. Ta lấy phần đối xứng với phần bên phải vừa giữ lại của (P1) qua trục tung.

4. Bài tập vận dụng (có đáp án)

Bài 1. Hãy vẽ đồ thị của hàm số bậc hai y = – 4x² + 8x – 3.

Hướng dẫn giải:

Đồ thị của hàm số bậc hai y = – 4x² + 8x – 3 có:

+ Đỉnh I (1 ; 1);

+ Trục đối xứng x = 1.

Giao điểm của đồ thị với trục tung là điểm A (0 ; – 3).

Điểm đối xứng với điểm A (0 ; – 3) qua trục đối xứng x = 1 là điểm D (2 ; – 3).

Giao điểm của đồ thị với trục hoành là điểm B ( ; 0) và điểm C ( ; 0).

Vì a = – 4 < 0, do đó đồ thị của hàm số bậc hai đã cho có bề lõm hướng xuống.

Ta vẽ đồ thị của hàm số bậc hai y = – 4x² + 8x – 3 như sau:

Bài 2. Cho hàm số y = x² + 4x + 3. Em hãy vẽ đồ thị của hàm số bậc hai đã cho.

Hướng dẫn giải:

Đồ thị của hàm số bậc hai y = x² + 4x + 3 có:

+ Đỉnh I (– 2 ; 1);

+ Trục đối xứng x = – 2.

Giao điểm của đồ thị với trục tung là điểm A (0 ; 3).

Điểm đối xứng với điểm A (0 ; 3) qua trục đối xứng x = 1 là điểm D (– 4 ; 3).

Giao điểm của đồ thị với trục hoành là điểm B (– 3 ; 0) và điểm C (– 1 ; 0).

Vì a = 1 > 0, do đó đồ thị của hàm số bậc hai đã cho có bề lõm hướng lên.

Ta vẽ đồ thị của hàm số bậc hai y = x² + 4x + 3 như sau:

Bài 3. Cho hàm số y = |x² + 4x + 3|. Em hãy vẽ đồ thị của hàm số đã cho.

Hướng dẫn giải:

Ta thực hiện vẽ đồ thị hàm số bậc hai y = x² + 4x + 3 (P₁) như ở bài 2.

Ta vẽ đồ thị hàm số bậc hai y = – (x² + 4x + 3) (P₂) bằng cách lấy phần đối xứng với (P₁) qua trục hoành và xóa đi các phần của (P₁) và (P₂) nằm ở phía dưới của trục hoành Ox. Ta được đồ thị của hàm số y = |x² + 4x + 3| (phần được tô đậm màu đỏ trong hình dưới) như sau:

Bài 4. Em hãy vẽ đồ thị của hàm số sau: y = |– 4x² + 8x – 3|.

Hướng dẫn giải:

Ta thực hiện vẽ đồ thị hàm số bậc hai y = – 4x² + 8x – 3 (P₁) như ở bài 1.

Ta vẽ đồ thị hàm số bậc hai y = – (– 4x² + 8x – 3) (P₂) bằng cách lấy phần đối xứng với (P₁) qua trục hoành và xóa đi các phần của (P₁) và (P₂) nằm ở phía dưới của trục hoành Ox. Ta được đồ thị của hàm số y = |– 4x² + 8x – 3| (phần được tô đậm màu đỏ trong hình dưới) như sau:

Bài 5. Em hãy vẽ đồ thị của hàm số sau: y = – 4x² + 8|x| – 3.

Hướng dẫn giải:

Ta thực hiện vẽ đồ thị hàm số bậc hai y = – 4x² + 8x – 3 (P₁) như ở bài 1.

Ta vẽ đồ thị hàm số y = – 4x² + 8|x| – 3 bằng cách giữ nguyên phần bên phải của (P₁) qua trục tung đồng thời xóa đi phần bên trái của (P₁) qua trục tung và lấy phần đối xứng với phần bên phải vừa giữ lại của (P₁) qua trục tung.

Ta được đồ thị của hàm số y = – 4x² + 8|x| – 3 (phần được tô đậm màu xanh trong hình dưới) như sau:

Ta thực hiện vẽ đồ thị hàm số bậc hai y = x² + 4x + 3 (P₁) như ở bài 2.

Ta vẽ đồ thị hàm số y = x² + 4|x| + 3 bằng cách giữ nguyên phần bên phải của (P₁) qua trục tung đồng thời xóa đi phần bên trái của (P₁) qua trục tung và lấy phần đối xứng với phần bên phải vừa giữ lại của (P₁) qua trục tung.

Ta được đồ thị của hàm số y = x² + 4|x| + 3 (phần được tô đậm màu xanh trong hình dưới) như sau:

 

5. Bài tập tự luyện (có đáp án)

Bài 1: Xác định phương trình của Parabol (P): y = x² + bx + c (P) trong các trường hợp sau:

a) (P) đi qua điểm A(1;0) và B (-2; -6)

b) (P) có đỉnh I(1; 4)

c) (P) cắt trục tung tại điểm có tung độ bằng 3 và có đỉnh S(-2; -1).

Bài 2: Lập bảng biến thiên và vẽ đồ thị các hàm số sau

a) y = x² - 3x + 2

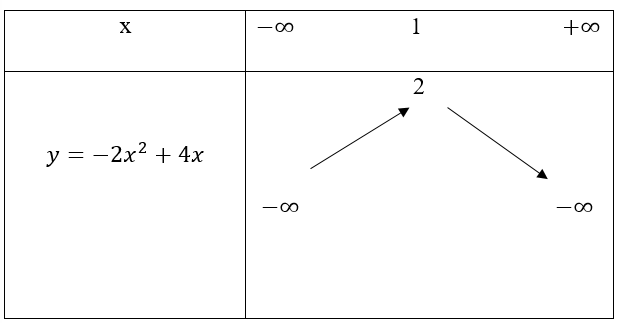
b) y = -2x² + 4x

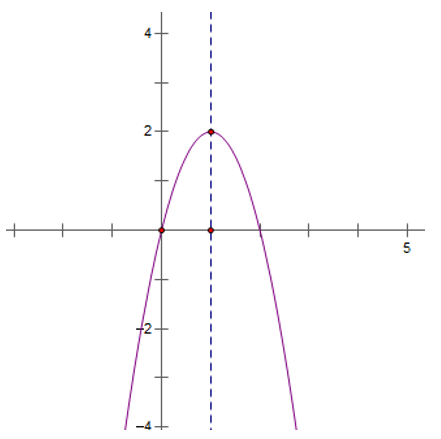
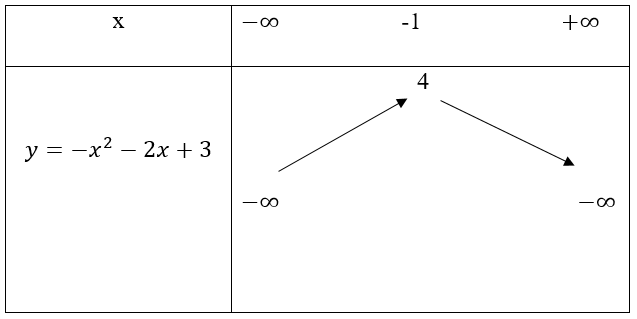
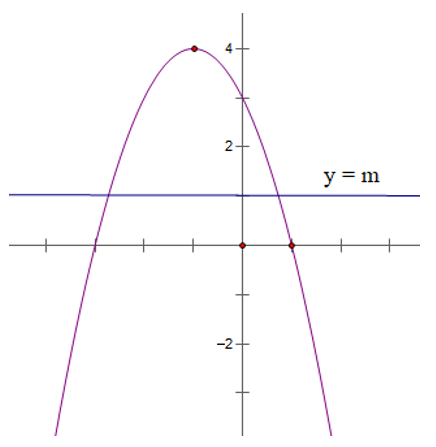
Bài 3: Cho hàm số y = -x² - 2x + 2

a) Lập bảng biến thiên và vẽ đồ thị các hàm số trên

b) Tìm m để đồ thị hàm số trên cắt đường thẳng y = m tại hai điểm phân biệt

c) Sử dụng đồ thị, hãy nêu các khoảng trên đó hàm số chỉ nhận giá trị âm

d) Sử dụng đồ thị, hãy tìm giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên [-3; 1]

Bài 4: Vẽ đồ thị của hàm số sau:

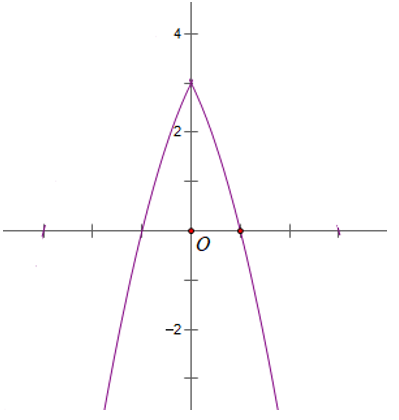
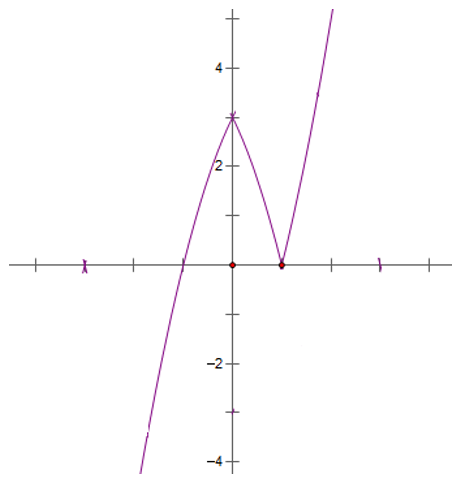
a) y = -x² - 2|x| + 3

b)

Bài 5: Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = x⁴ - 4x² - 1 trên [-1; 2]

Bài 6: Cho các số x, y thoả mãn: x² + y² = 1 + xy. Chứng minh rằng

            1/9 ≤ x⁴ + y⁴ - x²y² ≤ 3/2

Đáp án và hướng dẫn giải

Bài 1:

a) Vì (P) đi qua A, B nên

Vậy (P): y = x² + 3x - 4 .

b) Vì (P) có đỉnh I(1; 4) nên:

Vậy (P): y = x² - 2x + 5.

c) (P) cắt Oy tại điểm có tung độ bằng 3 suy ra c = 3

(P) có đỉnh S (-2; -1) suy ra:

Vậy (P): y = x² + 4x + 3.

Bài 2.

a) Ta có:

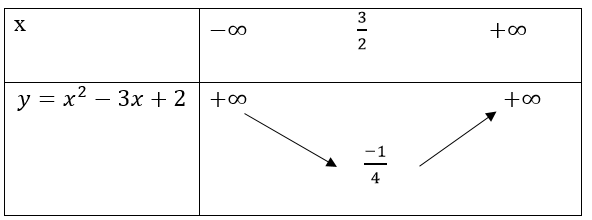
Bảng biến thiên

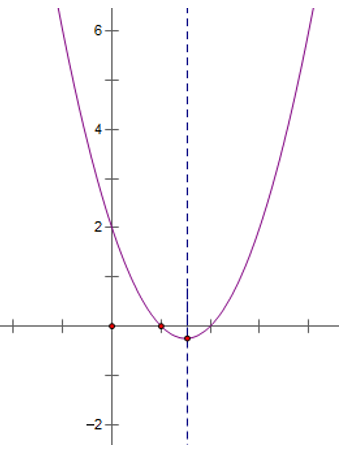
Suy ra đồ thị hàm số y = x² - 3x + 2 có đỉnh là I(3/2; -1/4), đi qua các điểm A(2; 0); B (1; 0), C(0; 2).

Đồ thị hàm số nhận đường thẳng x = 3/2 làm trục đối xứng và hướng bề lõm lên trên.

b) Ta có

Bảng biến thiên

Suy ra đồ thị hàm số y = -2x² + 4x có đỉnh là I(1; 2), đi qua các điểm O(0; 0), B (2; 0).

Đồ thị hàm số nhận đường thẳng x = 1 làm trục đối xứng và hướng bề lõm xuống dưới.

Bài 3:

a) Ta có:

Bảng biến thiên

Suy ra đồ thị hàm số y = -x² - 2x + 3 có đỉnh là I(-1; 4), đi qua các điểm A(1; 0), B (-3; 0).

Đồ thị hàm số nhận đường thẳng x = -1 làm trục đối xứng và hướng bề lõm xuống dưới.

b) Đường thẳng y = m song song hoặc trùng với trục hoành do đó dựa vào đồ thị ta có

Với m < 4 đường thẳng y = m và parabol y = -x² - 2x + 3 cắt nhau tại hai điểm phân biệt.

c) Hàm số nhận giá trị dương ứng với phần đồ thị nằm hoàn toàn trên trục hoành

Do đó hàm số chỉ nhận giá trị âm khi và chỉ khi x ∈ (-∞; -2) ∪ (1; +∞).

d) Dựa vào bảng biến thiên, ta có:

Bài 4: a) y = -x² - 2|x| + 3

a) Vẽ đồ thị hàm số (P): y = -x² - 2x + 3 có đỉnh I (-1; - 4), trục đối xứng x = -1, đi qua các điểm A(1; 0), B (-3; 0). Bề lõm hướng xuống dưới.

Khi đó (P₁ ) là đồ thị hàm số y = -x² - 2|x| + 3 là gồm phần bên phải trục tung của (P) và phần lấy đối xứng của nó qua trục tung.

b) Gọi (P₂ ) là phần đồ thị của (P) nằm trên trục hoành và lấy đối xứng của phần nằm dưới trục hoành qua trục Ox.

Vậy đồ thị hàm số

gồm phần bên đồ thị bên phải đường thẳng x = 1 của (P₂ ) và phần đồ thị bên trái đường thẳng x = 1 của (P₁ ).

Bài 5:

Đặt t = x². Với x ∈ [-1; 2] ta có t ∈ [0; 4]

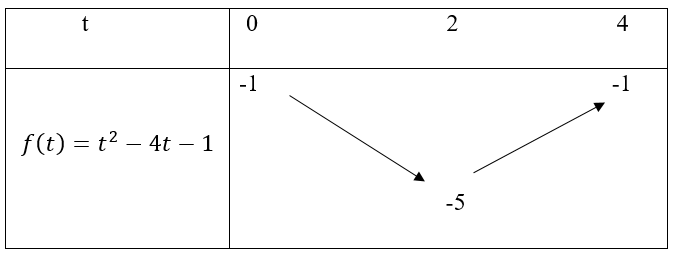
Hàm số trở thành f(t) = t² - 4t - 1 với t ∈ [0; 4].

Bảng biến thiên

Suy ra :

Bài 6:

Đặt P = x⁴ + y⁴ - x²y²

Ta có P = (x² + y²)² - 3x²y² = (1+xy)² - 3x²y² = -2x²y² + 2xy + 1

Đặt t = xy, khi đó P = -2t² + 2t + 1

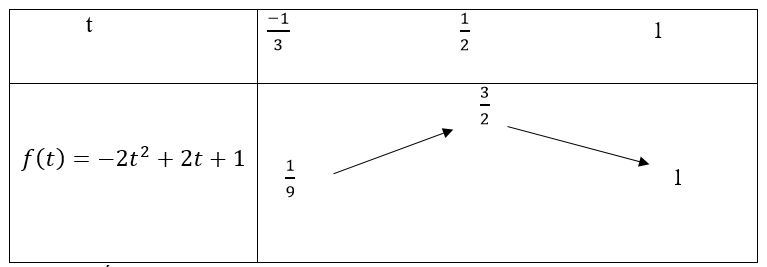
Xét hàm số f(t) = -2t² + 2t + 1 trên [(-1)/3; 1]

Ta có bảng biến thiên

Từ bảng biến thiên ta có :

Suy ra điều phải chứng minh.

Xem thêm các dạng bài tập Toán hay và chi tiết khác:

60 Bài tập về Khảo sát sự biến thiên và vẽ đồ thị hàm số (có đáp án năm 2023)

Cách khảo sát sự biến thiên và vẽ đồ thị của hàm số (2024) chi tiết và hay nhất

250 Bài tập hàm số bậc hai (có đáp án năm 2023)

150 Bài tập phương trình đường thẳng (2024) có đáp án

90 Bài tập về Vị trí tương đối giữa hai đường thẳng, góc và khoảng cách (2024) có đáp án