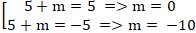Phương trình tiếp tuyến của đường tròn
Lý thuyết tổng hợp
1. Định nghĩa tiếp tuyến của đường tròn:
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính tại điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.
- Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
- Từ một điểm trên đường tròn ta có duy nhất một tiếp tuyến đi qua điểm đó. Từ một điểm ngoài đường tròn, ta có hai tiếp tuyến với đường tròn đi qua điểm đó.
2. Các công thức về Phương trình tiếp tuyến của đường tròn
- Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm M(x0;y0) thuộc đường tròn (C).
+ Nếu phương trình đường tròn có dạng x2+y2−2ax−2by+c=0 thì phương trình tiếp tuyến là: xx0+yy0−a(x+x0)−b(y+y0)+c=0.
+ Nếu phương trình đường tròn có dạng (x−a)2+(y−b)2=R2 thì phương trình tiếp tuyến là: (x−a)(x0−a)+(y−b)(y0−b)=R2
- Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm N(x0;y0) nằm ngoài đường tròn (C).
+ Viết phương trình của đường thẳng đi qua điểm N:
y−y0=m(x−x0)⇔mx−y−mx0+y0=0 (1)
+ Có d(I,d)=R ta tính được m thay m vào phương trình (1) ta được phương trình tiếp tuyến. Ta luôn tìm được hai đường tiếp tuyến.
Ví dụ minh họa
Bài 1: Cho đường tròn (C): (x−1)2+(y−1)2=5. Viết phương trình tiếp tuyến của (C) tại điểm B(-1; 2).
Lời giải:
Phương trình tiếp tuyến của (C) là:
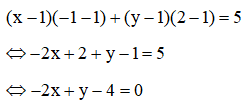
Bài 2: Cho đường tròn (C): (x−1)2+y2=18. Viết phương trình tiếp tuyến của (C) tại điểm A(-2; 3).
Lời giải:
Phương trình tiếp tuyến của (C) tại điểm A(-2; 3) là:
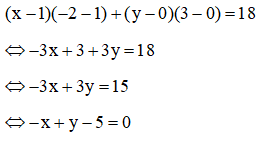
Bài 3: Cho đường tròn (C): (x−4)2+(y+3)2=2. Viết phương trình tiếp tuyến của (C) đi qua điểm C(4; 0).
Lời giải:
Gọi tiếp tuyến của (C) cần tìm là đường thẳng d
Ta có điểm C không thuộc đường tròn (C)
Phương trình đường thẳng đi qua điểm C là:
y−0=m(x−4)⇔mx−4m−y=0
Tâm của đường tròn (C) là I(4; -3) và bán kính R=√2
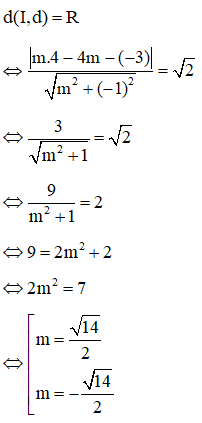
Với m=−√142, có phương trình tiếp tuyến là: √142x−4.√142−y=0
⇔√142x−y−2√14=0
Với m=−√142, có phương trình tiếp tuyến là: −√142x−4.(−√142)−y=0
⇔−√142x−y+2√14=0
Bài 4: Cho đường tròn (x - 3)2 + (y + 1)2 = 5 . Phương trình tiếp tuyến của ( C) song song với đường thẳng d : 2x + y + 7 = 0 là
A. 2x + y = 0; 2x + y - 10 = 0 B. 2x + y + 1 = 0 ; 2x + y - 1 = 0
C. 2x - y + 1 = 0; 2x + y - 10 = 0 D. 2x + y = 0; x + 2y - 10 = 0
Lời giải:
Do tiếp tuyến cần tìm song song với đường thẳng d: 2x + y + 7 = 0 nên
phương trình tiếp tuyến có dạng ∆: 2x + y + m = 0 với m ≠ 7 .
Đường tròn ( C) có tâm I( 3; -1) và bán kính R = √5
Đường thẳng tiếp xúc với đường tròn ( C) khi :
d( I , ∆) = R ⇔ 
⇔
Vậy ∆1 : 2x + y = 0 , ∆2 : 2x + y - 10 = 0
Chọn A.
Bài tập vận dụng (có đáp án )
Câu 1: Cho đường tròn( C): x2 + y2 - 2x + 8y - 23 = 0 và điểm M( 8; -3) . Độ di đoạn tiếp tuyến của ( C) xuất phát từ M là :
A. 10 B. 2√10 C. 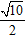
Câu 2: Cho đường tròn ( C ) : x2 + y2 - 3x - y = 0. Phương trình tiếp tuyến của ( C) tại M(1 ; -1) là:
A. x + 3y - 1 = 0 B. 2x - 3y + 1 = 0
C. 2x - y + 4 = 0 D. x + 3y + 2 = 0
Câu 3: Phương trình tiếp tuyến d của đường tròn (C): x2 + y2 - 3x-y= 0 tại điểm N(1;-1) là:
A. d: x + 3y - 2 = 0 B. d: x - 3y + 4 = 0
C. d: x - 3y - 4 = 0 D. d: x + 3y + 2 = 0
Câu 4: Cho đường tròn (x - 3)2 + (y - 1)2 = 10. Phương trình tiếp tuyến của ( C) tại điểm A( 4; 4) là
A. x - 3y + 5 = 0 B. x + 3y - 4 = 0
C. x - 3y + 16 = 0 D. x + 3y - 16 = 0
Câu 5: Cho đường tròn (C): x2 + y2 + 2x - 6y + 5 = 0 . Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y - 15 = 0 là
A. x + 2y = 0 và x + 2y - 10 = 0.
B. x - 2y = 0 và x - 2y + 10 = 0.
C. x + 2y - 12 = 0 và x + 2y + 22 = 0
D. x + 2y + 3 = 0 và x + 2y + 7 = 0
Câu 6: Cho đường tròn (x - 2)2 + (y - 2)2 = 9 . Phương trình tiếp tuyến của (C) đi qua điểm A( 5; -1) là
A. x + y - 4 = 0 và x - y - 2 = 0 .
B. x = 5 và y = -1.
C. 2x - y - 3 = 0 và 3x + 2y - 3 = 0.
D. 3x - 2y + 1 = 0 và 2x + 3y + 5 = 0
Câu 7: Cho đường tròn (C): (x−2)2+(y−3)2=16. Viết phương trình tiếp tuyến của (C) tại điểm B(2; 7).
Câu 8: Cho đường tròn (C): (x−4)2+(y+3)2=25. Viết phương trình tiếp tuyến của (C) đi qua điểm C(2; 3).
Xem thêm các dạng bài tập toán hay khác:
150 Bài tập phương trình đường thẳng (2024) có đáp án
2000 Bài tập Toán 10 phương pháp tọa độ trong mặt phẳng (có đáp án năm 2023)
250 Bài tập đường tròn trong mặt phẳng tọa độ (có đáp án năm 2023)
90 Bài tập về Vị trí tương đối giữa hai đường thẳng, góc và khoảng cách (2024) có đáp án
100 Bài tập về Phương trình quy về phương trình bậc hai (có đáp án năm 2023)