250 Bài tập đường tròn trong mặt phẳng tọa độ (có đáp án năm 2024) - Toán 10

Bài tập đường tròn trong mặt phẳng tọa độ

Kiến thức cần nhớ

1. Phương trình đường tròn

Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.

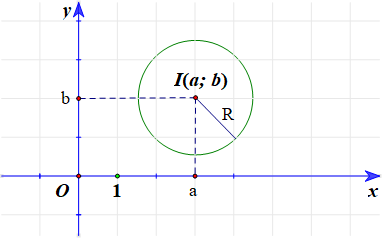
Phương trình (x – a)² + (y – b)² = R² được gọi là phương trình đường tròn tâm I(a; b), bán kính R.

Ví dụ 1: Viết phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm I(2; –3), bán kính R = 2.

b) (C) có đường kính AB với A(1; 6), B(–3; 2).

c) (C) đi qua ba điểm A(–2; 4), B(5; 5), C(6; –2).

Hướng dẫn giải

a) Đường tròn (C) có tâm I(2; –3), bán kính R = 2.

Vậy phương trình đường tròn (C): (x – 2)² +(y + 3)² = 4.

b) Gọi I(a; b) là tâm của đường tròn (C).

Vì đường tròn (C) có tâm I(a; b) và đường kính AB nên I là trung điểm AB.

Với A(1; 6), B(–3; 2).

Suy ra $\left\{\begin{array}{l}a=\frac{x_A+x_B}{2}=\frac{1-3}{2}=-1\\ b=\frac{y_A+y_B}{2}=\frac{6+2}{2}=4\end{array}\right.$

Khi đó ta có tọa độ I(–1; 4).

Ta có $\overrightarrow{IA}=\left(2;2\right)$.

Suy ra $R=IA=\left|\overrightarrow{IA}\right|=\sqrt{2^2+2^2}=2\sqrt{2}$.

Đường tròn (C) có tâm I(–1; 4), bán kính $R=2\sqrt{2}$.

Vậy phương trình đường tròn (C): (x + 1)² + (y – 4)² = 8.

c) Gọi M, N lần lượt là trung điểm của AB, AC.

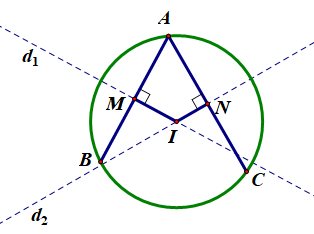
Ta có M là trung điểm AB với A(–2; 4), B(5; 5).

Suy ra $\left\{\begin{array}{l}{x}_M=\frac{x_A+x_B}{2}=\frac{-2+5}{2}=\frac{3}{2}\\ y_M=\frac{y_A+y_B}{2}=\frac{4+5}{2}=\frac{9}{2}\end{array}\right.$

Khi đó ta có $M\left(\frac{3}{2};\frac{9}{2}\right)$.

Tương tự, ta có N(2; 1).

Với A(–2; 4), B(5; 5), C(6; –2) ta có $\overrightarrow{AB}=\left(7;1\right),\overrightarrow{AC}=\left(8;-6\right)$.

Đường trung trực d₁ của đoạn thẳng AB đi qua điểm $M\left(\frac{3}{2};\frac{9}{2}\right)$, có vectơ pháp tuyến $\overrightarrow{AB}=\left(7;1\right)$.

Suy ra phương trình d₁: $7\left(x-\frac{3}{2}\right)+1\left(y-\frac{9}{2}\right)=0\iff 7x+y-15=0$.

Tương tự, ta có phương trình đường trung trực d₂ của đoạn thẳng AC:

8(x – 2) – 6(y – 1) = 0 ⇔ 4x – 3y – 5 = 0.

Vì đường tròn (C) có tâm I(a; b) và (C) đi qua ba điểm A, B, C nên IA = IB = IC (= R).

Vì IA = IB nên I nằm trên đường trung trực d₁ của đoạn thẳng AB.

Tương tự, ta có I nằm trên đường trung trực d₂ của đoạn thẳng AC.

Vì vậy ta suy ra I là giao điểm của d₁ và d₂.

Khi đó tọa độ điểm I là nghiệm của hệ phương trình:

$\left\{\begin{array}{l}7x+y-15=0\\ 4x-3y-5=0\end{array}\right.\iff \left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$

Suy ra I(2; 1).

Với I(2; 1) và A(–2; 4) ta có $\overrightarrow{IA}=\left(-4;3\right)$.

Suy ra $R=IA=\left|\overrightarrow{IA}\right|=\sqrt{{\left(-4\right)}^2+3^2}=5$.

Vậy phương trình đường tròn (C): (x – 2)² + (y – 1)² = 25.

Ví dụ 2: Tìm tâm và bán kính của đường tròn (C) có phương trình trong mỗi trường hợp sau:

a) (x – 4)² + (y – 10)² = 9.

b) (x + 2)² + (y – 5)² = 64.

c) x² + (y – 1)² = 36.

Hướng dẫn giải

a) (x – 4)² + (y – 10)² = 9

Đường tròn (C) có tâm I(4; 10), bán kính $R=\sqrt{9}=3$.

b) (x + 2)² + (y – 5)² = 64

Đường tròn (C) có tâm I(–2; 5), bán kính $R=\sqrt{64}=8$.

c) x² + (y – 1)² = 36.

Đường tròn (C) có tâm I(0; 1), bán kính $R=\sqrt{36}=6$.

Nhận xét: Ta có (x – a)² + (y – b)² = R²

⇔ x² + y² – 2ax – 2by + (a² + b² – R²) = 0.

Vậy phương trình đường tròn (x – a)² + (y – b)² = R² có thể được viết dưới dạng x² + y² – 2ax – 2by + c = 0, trong đó c = a² + b² – R².

Ngược lại, phương trình x² + y² – 2ax – 2by + c = 0 là phương trình của đường tròn (C) khi và chỉ khi a² + b² – c > 0. Khi đó đường tròn (C) có tâm I(a; b) và bán kính $R=\sqrt{a^2+b^2-c}$.

Ví dụ 3: Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Nếu là phương trình đường tròn, hãy tìm tọa độ tâm và bán kính của đường tròn đó.

a) x² + y² + 2x – 6y – 15 = 0.

b) 2x² + 2y² + 4x + 8y + 14 = 0.

Hướng dẫn giải

a) Phương trình đã cho có dạng: x² + y² – 2ax – 2by + c = 0, với a = –1, b = 3, c = –15.

Ta có a² + b² – c = 1 + 9 + 15 = 25 > 0.

Vậy phương trình đã cho là phương trình đường tròn có tâm I(–1; 3), bán kính R = 5.

b) Ta có 2x² + 2y² + 4x + 8y + 14 = 0 ⇔ x² + y² + 2x + 4y + 7 = 0.

Phương trình trên có dạng x² + y² – 2ax – 2by + c = 0, với a = –1, b = –2, c = 7.

Ta có a² + b² – c = 1 + 4 – 7 = –2 < 0.

Vậy phương trình đã cho không phải là phương trình đường tròn.

2. Phương trình tiếp tuyến của đường tròn

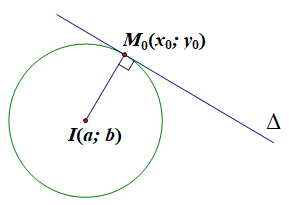
Phương trình tiếp tuyến của đường tròn tâm I(a; b) tại điểm M₀(x₀; y₀) nằm trên đường tròn là:

(a – x₀)(x – x₀) + (b – y₀)(y – y₀) = 0.

Ví dụ 1: Viết phương trình tiếp tuyến d của đường tròn (C): (x – 2)² + (y + 3)² = 5 tại điểm M(3; –1).

Hướng dẫn giải

Ta có (3 – 2)² + (–1 + 3)² = 5.

Suy ra M ∈ (C).

Đường tròn (C) có tâm I(2; –3).

Phương trình tiếp tuyến d của đường tròn (C) tại điểm M(3; –1) là:

(2 – 3)(x – 3) + [–3 – (–1)].[y – (–1)] = 0.

⇔ –1.(x – 3) + (–2).(y + 1) = 0.

⇔ –x – 2y + 1 = 0.

Vậy phương trình tiếp tuyến d của đường tròn (C) cần tìm là –x – 2y + 1 = 0.

Các dạng bài tập đường tròn trong mặt phẳng tọa độ

(Xem chi tiết trong file đính kèm)

Hệ thống bài tập

+ Dạng 1. Nhận dạng phương trình đường tròn. Tìm tâm và bán kính đường tròn.

+ Dạng 2. Viết phương trình đường tròn.

+ Dạng 3. Vị trí tương đối của điểm; đường thẳng; đường tròn với đường tròn.

+ Dạng 4. Viết phương trình tiếp tuyến với đường tròn.

Hệ thống bài tập trắc nghiệm

+ Dạng 1. Nhận dạng phương trình đường tròn.

+ Dạng 2. Tìm tọa độ tâm, bán kính đường tròn.

+ Dạng 3. Viết phương trình đường tròn.

+ Dạng 4. Tương giao của đường thẳng và đường tròn.

+ Dạng 5. Câu hỏi MIN – MAX.

Bài tập (có hướng dẫn giải)

1. Bài tập vận dụng

Bài 1. Lập phương trình đường tròn (C) trong các trường hợp sau:

a) (C) đi qua ba điểm A(–1; 3), B(1; 4), C(3; 2).

b) (C) có tâm I(–1; 2) và tiếp xúc với đường thẳng ∆: x – 2y + 7 = 0.

c) (C) có tâm thuộc đường thẳng d: 2x – y – 5 = 0 và đi qua hai điểm A(1; 2), B(4; 1).

Hướng dẫn giải

a) Gọi M, N lần lượt là trung điểm của AB, AC.

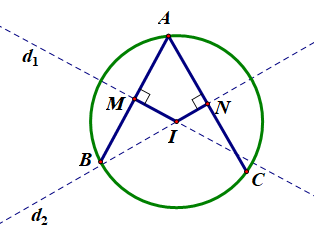
Ta có M là trung điểm AB với A(–1; 3), B(1; 4).

Suy ra $\left\{\begin{array}{l}{x}_M=\frac{x_A+x_B}{2}=\frac{-1+1}{2}=0\\ y_M=\frac{y_A+y_B}{2}=\frac{3+4}{2}=\frac{7}{2}\end{array}\right.$

Khi đó ta có $M\left(0;\frac{7}{2}\right)$.

Tương tự, ta có $N\left(1;\frac{5}{2}\right)$.

Với A(–1; 3), B(1; 4), C(3; 2) ta có $\overrightarrow{AB}=\left(2;1\right),\overrightarrow{AC}=\left(4;-1\right)$.

Đường trung trực d₁ của đoạn thẳng AB đi qua điểm $M\left(0;\frac{7}{2}\right)$, có vectơ pháp tuyến $\overrightarrow{AB}=\left(2;1\right)$.

Suy ra phương trình d₁: $2\left(x-0\right)+1\left(y-\frac{7}{2}\right)=0\iff 2x+y-\frac{7}{2}=0$.

Tương tự, ta có phương trình đường trung trực d₂ của đoạn thẳng AC:

$4\left(x-1\right)-1\left(y-\frac{5}{2}\right)=0\iff 4x-y-\frac{3}{2}=0$.

Vì đường tròn (C) có tâm I(a; b) và (C) đi qua ba điểm A, B, C nên IA = IB = IC (= R).

Vì IA = IB nên I nằm trên đường trung trực d₁ của đoạn thẳng AB.

Tương tự, ta có I nằm trên đường trung trực d₂ của đoạn thẳng AC.

Vì vậy I là giao điểm của d₁ và d₂.

Khi đó tọa độ điểm I là nghiệm của hệ phương trình:

$\left\{\begin{array}{l}2x+y-\frac{7}{2}=0\\ 4x-y-\frac{3}{2}=0\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{5}{6}\\ y=\frac{11}{6}\end{array}\right.$

Suy ra $I\left(\frac{5}{6};\frac{11}{6}\right)$.

Với $I\left(\frac{5}{6};\frac{11}{6}\right)$ và A(–1; 3) ta có $\overrightarrow{IA}=\left(-\frac{11}{6};\frac{7}{6}\right)$.

Suy ra $R=IA=\left|\overrightarrow{IA}\right|=\sqrt{{\left(-\frac{11}{6}\right)}^2+{\left(\frac{7}{6}\right)}^2}=\frac{\sqrt{170}}{6}$.

Vậy phương trình đường tròn (C): ${\left(x-\frac{5}{6}\right)}^2+{\left(y-\frac{11}{6}\right)}^2=\frac{85}{18}$.

b) (C) có tâm I(–1; 2) và tiếp xúc với đường thẳng ∆: x – 2y + 7 = 0.

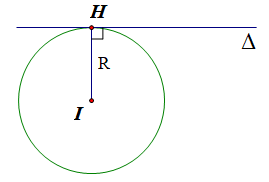
Vì (C) tiếp xúc với đường thẳng ∆ nên ta có:

R = d(I, ∆) = $\frac{\left|-1-2.2+7\right|}{\sqrt{1^2+{\left(-2\right)}^2}}=\frac{2\sqrt{5}}{5}$.

Vậy phương trình đường tròn (C): ${\left(x+1\right)}^2+{\left(y-2\right)}^2=\frac{4}{5}$.

c) (C) có tâm thuộc đường thẳng d: 2x – y – 5 = 0 và đi qua hai điểm A(1; 2), B(4; 1).

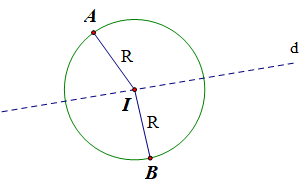
Phương trình đường thẳng d: 2x – y – 5 = 0 ⇔ y = 2x – 5.

Giả sử I(a; b).

Vì I ∈ d nên ta có I(a; 2a – 5).

Với A(1; 2), B(4; 1) và I(a; 2a – 5) ta có:

$\overrightarrow{AI}=\left(a-1;2a-7\right),\overrightarrow{BI}=\left(a-4;2a-6\right)$.

Vì đường tròn (C) đi qua hai điểm A(1; 2), B(4; 1).

Ta suy ra AI = BI (= R).

⇔ AI² = BI².

⇔ (a – 1)² + (2a – 7)² = (a – 4)² + (2a – 6)²

⇔ a² – 2a + 1 + 4a² – 28a + 49 = a² – 8a + 16 + 4a² – 24a + 36

⇔ 2a = 2.

⇔ a = 1.

Với a = 1, ta có b = 2a – 5 = 2.1 – 5 = –3.

Suy ra I(1; –3), bán kính R = AI = $\sqrt{{\left(1-1\right)}^2+{\left(2.1-7\right)}^2}$ = 5.

Vậy phương trình đường tròn (C): (x – 1)² + (y + 3)² = 25.

Bài 2. Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Nếu là phương trình đường tròn, hãy tìm tâm và bán kính của đường tròn đó.

a) x² + y² + 2x – 4y + 9 = 0.

b) x² + y² – 6x + 4y + 13 = 0.

c) 2x² + 2y² – 6x – 4y – 1 = 0.

d) 2x² + y² + 2x – 3y + 9 = 0.

Hướng dẫn giải

a) Phương trình đã cho có dạng: x² + y² – 2ax – 2by + c = 0, với a = –1, b = 2, c = 9.

Ta có a² + b² – c = 1 + 4 – 9 = –4 < 0.

Vì vậy phương trình đã cho không phải là phương trình đường tròn.

b) Phương trình đã cho có dạng: x² + y² – 2ax – 2by + c = 0, với a = 3, b = –2, c = 13.

Ta có a² + b² – c = 9 + 4 – 13 = 0.

Vì vậy phương trình đã cho không phải là phương trình đường tròn.

c) Ta có 2x² + 2y² – 6x – 4y – 1 = 0.

$\iff x^2+y^2-3x-2y-\frac{1}{2}=0$.

Phương trình trên có dạng: x² + y² – 2ax – 2by + c = 0, với $a=\frac{3}{2}$, b = 1, $c=-\frac{1}{2}$.

Ta có $a^2+b^2-c=\frac{9}{4}+1+\frac{1}{2}=\frac{15}{4}$> 0.

Vì vậy phương trình đã cho là phương trình đường tròn.

Đường tròn có tâm $I\left(\frac{3}{2};1\right)$, bán kính $R=\frac{\sqrt{15}}{2}$.

d) Phương trình đã cho không có dạng: x² + y² – 2ax – 2by + c = 0.

Vậy phương trình đã cho không phải là phương trình đường tròn.

Bài 3. Lập phương trình tiếp tuyến d của đường tròn (C) trong các trường hợp sau:

a) (C): x² + y² – 2x = 0 tại điểm M(1; 1).

b) (C): x² + y² – 2x + 4y + 4 = 0, biết rằng tiếp tuyến vuông góc với đường thẳng ∆: x + 2y + 5 = 0.

Hướng dẫn giải

a) Phương trình (C) có dạng: x² + y² – 2ax – 2by + c = 0, với a = 1, b = c = 0.

Ta có a² + b² – c = 1 + 0 – 0 = 1 > 0.

Vì vậy phương trình (C) đã cho là phương trình đường tròn.

Đường tròn (C) có tâm I(1; 0).

Ta có 1² + 1² – 2.1 = 0.

Suy ra M ∈ (C).

Phương trình tiếp tuyến d của đường tròn (C) tại điểm M(3; –1) là:

(1 – 3)(x – 3) + (0 + 1).(y + 1) = 0.

⇔ –2.(x – 3) + y – 1 = 0.

⇔ –2x + y + 5 = 0.

Vậy phương trình tiếp tuyến cần tìm là –2x + y + 5 = 0.

b) Phương trình (C) có dạng: x² + y² – 2ax – 2by + c = 0, với a = 1, b = –2, c = 4.

Ta có a² + b² – c = 1 + 4 – 4 = 1 > 0.

Vì vậy phương trình (C) đã cho là phương trình đường tròn.

Đường tròn (C) có tâm I(1; –2), bán kính R = 1.

Gọi d là tiếp tuyến cần tìm.

Gọi k_d là hệ số góc của d.

Phương trình ∆: x + 2y + 5 = 0 $\iff y=-\frac{1}{2}x-\frac{5}{2}$.

Suy ra ∆ có hệ số góc $k_{\Delta }=-\frac{1}{2}$.

Ta có d ⊥ ∆.

Suy ra k_d.k_∆ = –1.

$\iff k_d.\left(-\frac{1}{2}\right)=-1$.

⇔ k_d = 2.

Khi đó phương trình d có dạng: y = 2x + m hay 2x – y + m = 0.

Ta có d là tiếp tuyến của đường tròn (C).

Ta suy ra d(I, d) = R.

$\iff \frac{\left|2.1-\left(-2\right)+m\right|}{\sqrt{2^2+{\left(-1\right)}^2}}=1$.

$\iff \left|m+4\right|=\sqrt{5}$

$\iff m+4=\sqrt{5}$ hoặc $m+4=-\sqrt{5}$

$\iff m=-4+\sqrt{5}$ hoặc $m=-4-\sqrt{5}$.

Vậy có 2 tiếp tuyến d thỏa yêu cầu bài toán có phương trình là $2x-y-4+\sqrt{5}=0$ và $2x-y-4-\sqrt{5}=0$.

2. Bài tập tự luyện

(Xem trong file đính kèm)

Xem thêm các dạng bài tập toán hay khác:

150 Bài tập phương trình đường thẳng (2024) có đáp án

2000 Bài tập Toán 10 phương pháp tọa độ trong mặt phẳng (có đáp án năm 2023)

250 Bài tập đường tròn trong mặt phẳng tọa độ (có đáp án năm 2023)

90 Bài tập về Vị trí tương đối giữa hai đường thẳng, góc và khoảng cách (2024) có đáp án

100 Bài tập về Phương trình quy về phương trình bậc hai (có đáp án năm 2023)