Bài tập các khái niệm mở đầu
Kiến thức cần nhớ
1. KHÁI NIỆM VECTƠ
+) Vecto là một đoạn thẳng có hướng.
Ví dụ 1: i) vecto →AB: (đọc là vecto AB) 
ii) Vecto →BA: 
iii) vecto →u: 
+) Độ dài của vecto là khoảng cách giữa điểm đầu và điểm cuối của vecto đó.
Kí hiệu: độ dài của vecto →AB là |→AB|.
Ví dụ 2: |→AB|=AB;|→DE|=DE
+) Vecto không, là vecto có độ dài bằng 0. Ví dụ: →AA,→EE,...(điểm đầu trùng điểm cuối)
Kí hiệu chung là →0.
2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU
+) Giá của vecto: là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.
Ví dụ: Giá của vecto →CD là đường thẳng CD
+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.
Ví dụ:
Ba vecto →u,→CD,→AB cùng phương.
Trong đó 2 vecto →u,→CD cùng hướng, còn 2 vecto →CD,→AB ngược hướng.
+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.
* Chú ý:
- Chỉ khi hai vecto cùng phương ta mới nói tới chúng cùng hướng hay ngược hướng.
- Vecto →0 cùng phương, cùng hướng với mọi vecto.
- Với mỗi điểm O và vecto →a cho trước, có duy nhất điểm A sao cho →OA=→a
* Nhận xét:
+) Ba điểm A, B, C thẳng hàng khi và chỉ khi →AB và →AC cùng phương.
+) Ba điểm A, B, C thẳng hàng, B nằm giữa khi và chỉ khi →AB và →AC cùng hướng.
Các dạng bài tập hàm số
Dạng 1. Xác định một vectơ; phương, hướng của vectơ; độ dài của vectơ.
+ Xác định một vectơ và xác sự cùng phương, cùng hướng của hai vectơ theo nghĩa.
+ Dựa vào các tình chất hình học của các hình đã cho biết để tính độ dài của một vectơ.
Dạng 2. Chứng minh hai vectơ bằng nhau.
+ Để chứng minh hai vectơ bằng nhau ta chứng minh chúng có cùng độ dài và cùng hướng hoặc dựa vào nhận xét nếu tứ giác ABCD là hình bình hành thì AB = DC hoặc AD = BC.
Dạng 3. Xác định điểm thoả đẳng thức vectơ.
+ Sử dụng: Hai véctơ bằng nhau khi và chỉ khi chúng cùng độ dài và cùng hướng.
Bài tập (có đáp án)
1. Bài tập vận dụng
B1. Bài tập trắc nghiệm
Câu 1. Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
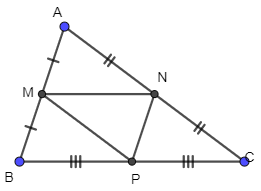
Phát biểu nào dưới đây là sai.
A. →MN=→PC ;
B. →AA cùng hướng với →PP ;
C. →MB=→AM ;
D. →MN=→PB .
Hướng dẫn giải
Đáp án đúng là D
+) Xét tam giác ABC, có:
M là trung điểm AB
N là trung điểm của AC
⇒ MN là đường trung bình của tam giác ABC
⇒ MN // BC và MN = 12 BC
Mà BP = PC = 12 BC (P là trung điểm của BC)
⇒ MN = CP = PB (1)
Vì MN // BC nên MN // CP. Khi đó →MN và →PC cùng phương. Suy ra →MN và →PC cùng hướng (2)
Từ (1) và (2) suy ra →MN = →PC . Do đó đáp án A đúng.

Câu 2. Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ →AB .
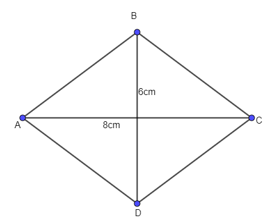
A. 10 cm;
B. 3 cm;
C. 4 cm;
D. 5cm.
Hướng dẫn giải
Đáp án đúng là D
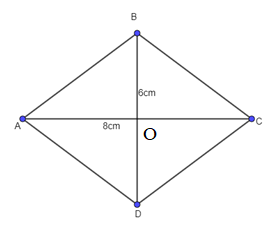
Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó O là trung điểm của AC, cũng là trung điểm của BD.
⇒ AO = OC = AC2=82=4cm.
⇒ BO = OD = BD2=62=3cm.
Xét tam giác AOB vuông tại O, có:
AB2 = AO2 + BO2 (định lí Py – ta – go)
⇔ AB2 = 42 + 32 = 16 + 9 = 25
⇔ AB = 5 (cm)
⇒|→AB|=AB=5cm.
Vậy độ dài →AB là 5cm.
Câu 3. Cho hình vẽ sau:
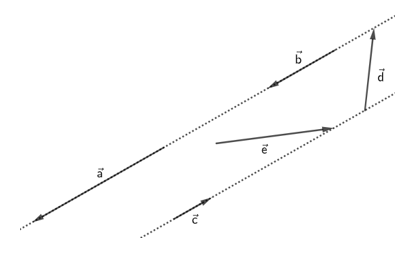
Cặp vectơ nào cùng hướng?
Hướng dẫn giải
Đáp án đúng là A

B2. Bài tập tự luận
Câu 4. Cho hình vẽ:
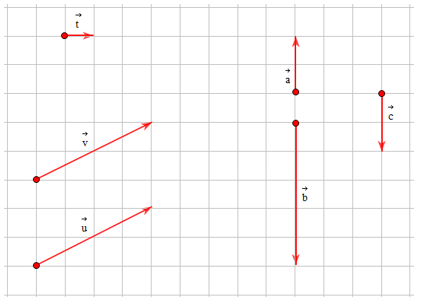
a) Chỉ ra các vectơ cùng phương.
b) Chỉ ra các vectơ cùng hướng, ngược hướng.
c) Chỉ ra các vectơ bằng nhau.
Hướng dẫn giải
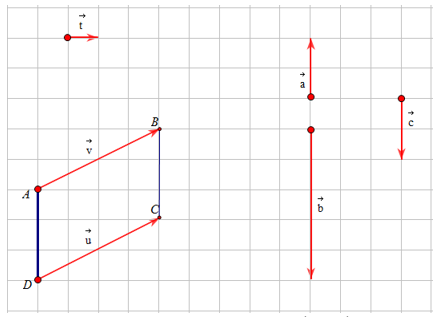
a) Ta nối các điểm đầu và điểm cuối của hai vectơ →uvà →vđể được tứ giác ABCD.
Xét tứ giác ABCD có:
AD // BC (vì AD và BC nằm trên hai dòng kẻ phân biệt)
AD = BC (cùng bằng 3 đơn vị)
Suy ra ABCD là hình bình hành.
Suy ra AB // DC.
Khi đó, ta có giá của hai vectơ →u và →v song song với nhau nên hai vectơ →u và →v cùng phương.
Ba vectơ →a, →b, →c có giá nằm trên các dòng kẻ dọc nên giá của các vectơ này trùng nhau hoặc song song, vì vậy ba vectơ này cùng phương.
Vectơ →t không cùng phương với vectơ nào.
Vậy, hai vectơ →u và →v là hai vectơ cùng phương ; ba vectơ →a, →b, →c đôi một cùng phương.
b) Hai vectơ →u và →v cùng hướng.
Hai vectơ →a và →b ngược hướng.
Hai vectơ →a và →c ngược hướng.
Hai vectơ →b và →c cùng hướng.
Vậy các cặp vectơ cùng hướng là: →u và →v; →b và →c. Các cặp vectơ ngược hướng là: →a và →b; →a và →c.
c) Vì ABCD là hình bình hành nên AB = DC.
Hai vectơ →u và →v cùng hướng. Mặt khác |→u|=DC; |→v|=AB, suy ra |→u|=|→v| .
Vậy, →u = →v.
Hai vectơ và cùng hướng, tuy nhiên không cùng độ dài: |→b|=5, |→c|=2. Vì vậy →b và →c không bằng nhau.
Câu 5. Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi →AB=→DC .
Hướng dẫn giải
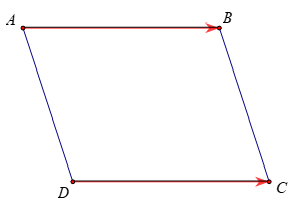
– Giả sử ABCD là hình bình hành. Khi đó AB // DC và AB = DC.
Vì AB // DC nên →AB và →DC cùng phương. Từ hình vẽ dễ thấy →AB và →DC cùng hướng.
Vì AB = DC nên |→AB|=|→DC|.
Vậy →AB = →DC.
– Giả sử →AB = →DC. Khi đó →AB và →DC cùng hướng và |→AB|=|→DC|.
Từ →AB và →DC cùng hướng suy ra chúng cùng phương, hay AB // DC.
Từ |→AB|=|→DC| suy ra AB = DC.
Vậy ABCD là hình bình hành.
Vậy tứ giác ABCD là một hình bình hành khi và chỉ khi →AB = →DC.
2. Bài tập tự luyện có hướng dẫn
Xem thêm các dạng bài tập liên quan khác:
200 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)
100 Bài tập hệ bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)
500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2023)
60 Bài tập về Bất phương trình mũ và bất phương trình logarit (2024) có đáp án
300 Bài tập Toán 8 chương 4: Bất phương trình bậc nhất một ẩn (có đáp án năm 2023)