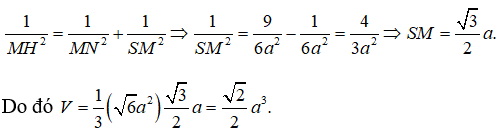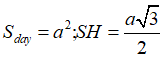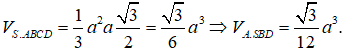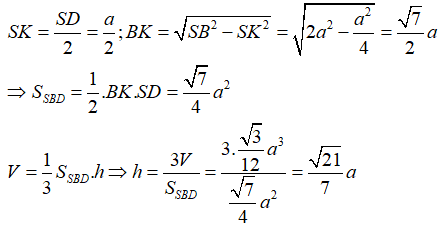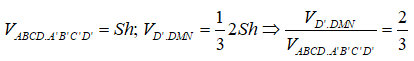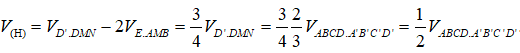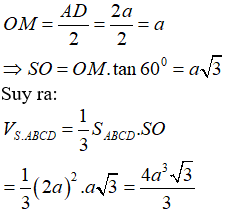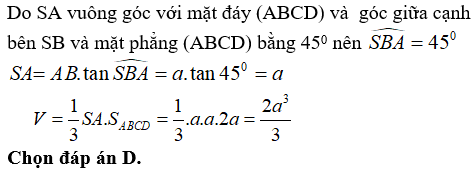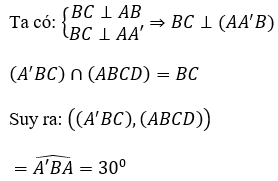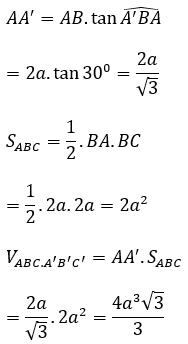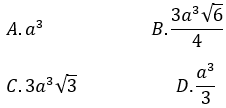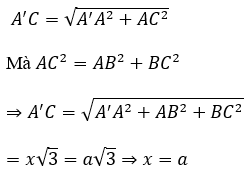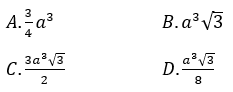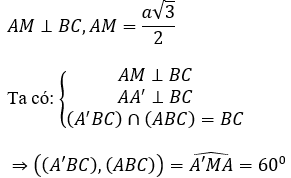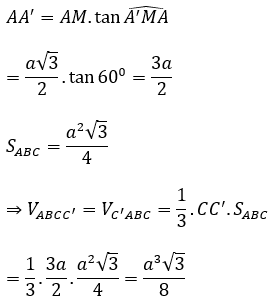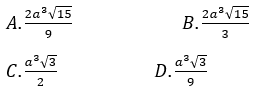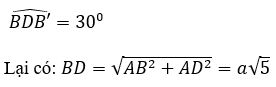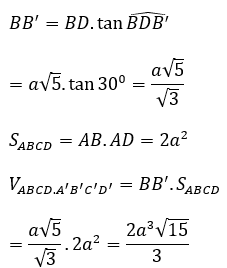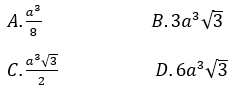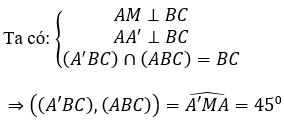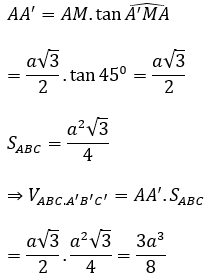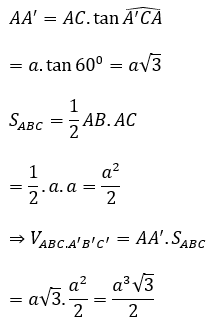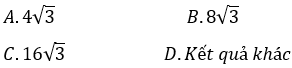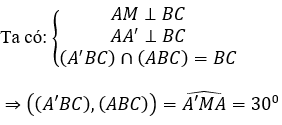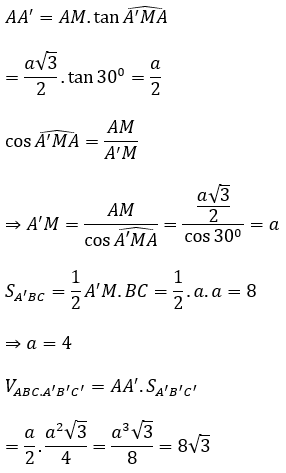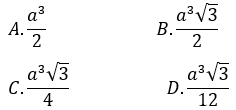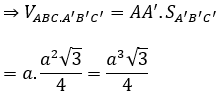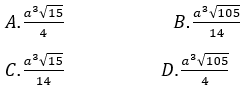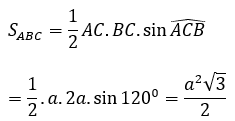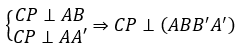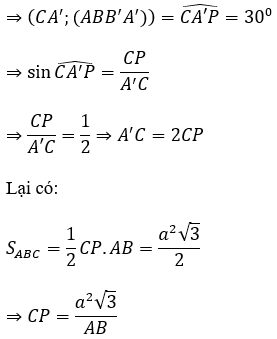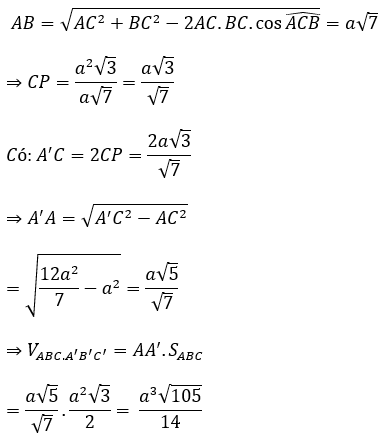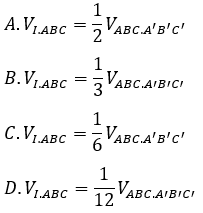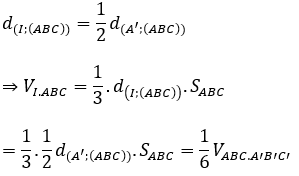Thể tích khối đa diện
Kiến thức cơ bản
1. Khái niệm về thể tích của khối đa diện
Người ta chứng minh được rằng: có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất V(H) thỏa mãn các tính chất sau:
a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) = 1.
b) Nếu hai khối đa diện (H1) và (H2) bằng nhau thì V(H1) = V(H2).
c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì:
V(H) = V(H1) + V(H2).
Số dương V(H) nói trên được gọi là thể tích của khối đa diện (H). Số đó cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H).
Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.
- Định lí : Thể tích của khối hình chữ nhật bằng tích ba kích thước của nó.
2. Thể tích của khối lăng trụ
Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
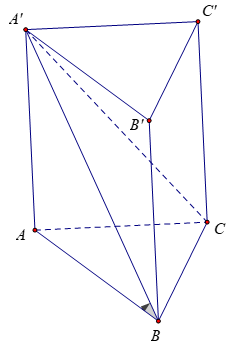
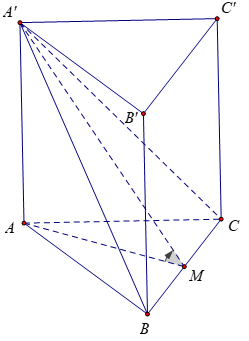
Ví dụ 1. Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều cạnh a = 4 và biết diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ.
Lời giải:

3. Thể tích khối chóp
Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là: .
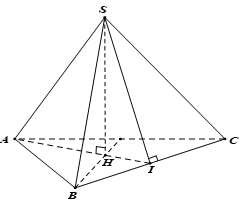
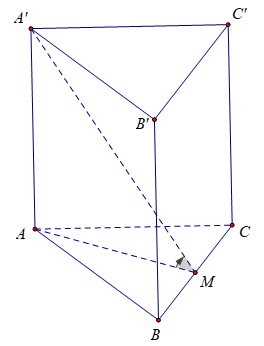
Ví dụ 2. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC và (SBC) hợp với đáy (ABC) một góc 60o. Tính thể tích hình chóp.
Lời giải:
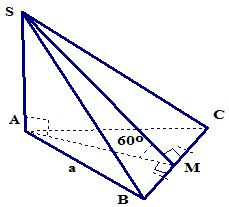
Gọi M là trung điểm của BC.
Vì tam giác ABC đều nên AMBCSABC (định lí 3 đường vuông góc).
Vậy góc[(SBC);(ABC)] =
Tam giác ABC đều cạnh a nên đường cao
Xét tam giác SAM có : SA = AM.tan600 =
Vậy V =
Các dạng bài tập về thể tích khối đa diện
(Xem thêm trong file pdf)
Dạng 1 Biết chiều cao và diện tích đáy
Dạng 2 Thể tích khối lăng trụ đứng
Dạng 3 Thể tích khối lăng trụ xiên
Bài tập có hướng dẫn
1. Bài tập vận dụng
Câu 1: Cho hình chóp S.ABCD có đáy là hình chữ nhật, hình chiếu của S lên đáy trùng với trung điểm của AB. Tính thể tích V của hình chóp đã cho, biết rằng AB = a, BC = a , khoảng cách từ A đến mặt (SCD) bằng
Lời giải:
Gọi M, N lần lượt là trung điểm của AB, CD, H là chân đường vuông góc kẻ từ M tới SN. Khi đó SM ⊥ (ABCD). Vì AB // CD nên AB // (ABCD), do đó d(A, (SCD)) = d(M, (SCD)) = MH
Ta có
Câu 2: Cho hình chóp S.ABCD, có đáy là hình vuông cạnh a, SCD là tam giác đều và (SCD) vuông góc với đáy. Tính khoảng cách h từ A đến mặt phẳng (SBD).
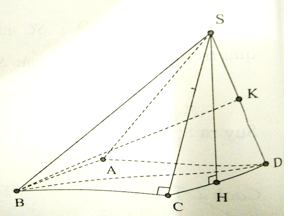
Lời giải:
Gọi H là trung điểm của CD, dễ thấy SH là đường cao của hình chóp.
Suy ra
Để ý rằng SB2 = SH2 + BH2 = SH2 + BC2 + CH2 = + a2 + = 2a2.
Suy ra BS = BD = a, gọi K là trung điểm của SD ta có:
Câu 3: Cho hình hộp ABCD.A'B'C'D'. Gọi E, F tương ứng là trung điểm của các cạnh A’A, C’C. Gọi M = (D'E) ∩ (DA), N = (D'F) ∩ (DC). Tính tỉ số giữa thể tích hình chóp D’.DMN và thể tích hình hộp ABCD.A'B'C'D'
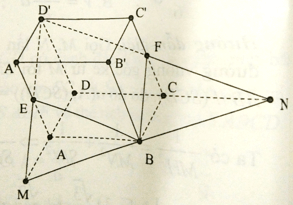
Lời giải:
Dễ thấy MN đi qua B, MD = 2AD, ND = 2CD. Hình chóp và hình hộp nói trên có chung chiều cao h .
Nếu diện tích đáy của hình hộp bằng S thì diện tích đáy của hình chóp bằng 2S.
Ta có:
Câu 4: Cho hình hộp ABCD.A'B'C'D'. Gọi E, F tương ứng là trung điểm các cạnh A’A, C’C. Mặt phẳng (D’EF) chia hình hộp thành hai hình đa diện. Gọi (H) là hình đa diện chứa đỉnh A, (H’) là hình đa diện còn lại. Tính tỉ số k giữa thể tích hình (H) và thể tích hình (H’).
Lời giải:
Gọi M = (D'E) ∩ (DA), N = (D'F) ∩ (DC). Dễ thấy MN đi qua B, các hình chóp E.AMB và F.CNB có diện tích đáy và chiều cao bằng nhau. Áp dụng công thức (7) ta có :
Áp dụng ví dụ 9, ta có :
Suy ra V(H) = V(H'). Do đó k = 1 .
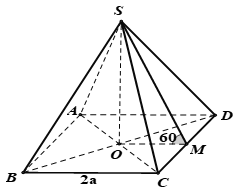
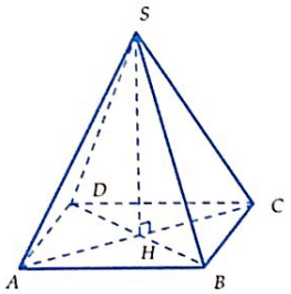
Câu 5: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60°. Tính theo a thể tích khối chóp S.ABCD
Lời giải:
Gọi O là tâm hình vuông ABCD, M là trung điểm CD.
Khi đó SO là đường cao hình chóp, góc là góc giữa mặt bên và mặt đáy của hình chóp.
Chọn đáp án A.
Câu 6: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a. Mặt bên tạo với mặt đáy một góc 60°. Tính thể tích V của hình chóp S.ABC.
Lời giải:
Gọi H là tâm của tam giác ABC. Trong (SBC), kẻ SI vuông góc BC.
Do góc giữa mặt bên và mặt đáy là 600 suy ra
Câu 7: Khối chóp đều S.ABCD có tất cả các cạnh đều bằng a. Khi đó độ dài đường cao h của khối chóp là:
Lời giải:
Gọi O là tâm của hình vuông ABCD.
Ta có : OA = OB = OC = OD và SA = SB = SC = SD
Suy ra : SO là trục đường tròn ngoại tiếp ABCD
⇒ SO ⊥ (ABCD)
Ta có :
Câu 8: Hình chóp tứ giác đều có tất cả các cạnh bằng a. Thể tích khối chóp đó bằng?
Lời giải:
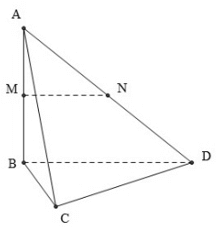
Câu 9: Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau: BA = 3a, BC =BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD Tính thể tích khối chóp C.BDNM
Lời giải:
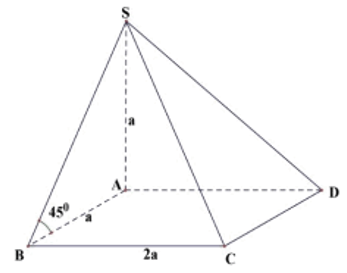
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45°. Thể tích hình chóp S.ABCD bằng?
Lời giải:
Câu 11. Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại B. Biết và . Tính thể tích khối lăng trụ ABC.A’B’C’
Lời giải:
Ta có vuông cân tại B nên
ABC.A’B’C’ là lăng trụ đứng nên . Do đó vuông tại C
Áp dụng định lí Pytago ta được:
Diện tích bằng
Suy ra :
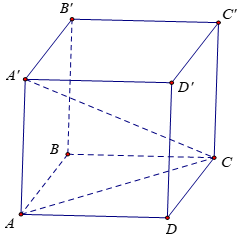
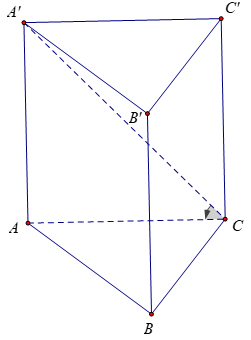
Câu 12. Cho lăng trụ đều ABC.A’B’C’ cạnh a. Góc giữa A’B với đáy bằng . Tính thể tích khối lăng trụ.
Lời giải:
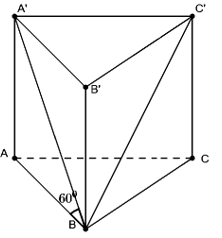
Do ABC.A’B’C’ là lăng trụ đều nên và ABC là tam giác đều
Ta có :
Diện tích tam giác đều ABC là
Do đó thể tích lăng trụ là :
Câu 13. Cho lăng trụ xiên ABC.A’B’C’ có đáy là tam giác đều cạnh a. Cạnh bên bằng và hợp với đáy một góc bằng . Thể tích của lăng trụ bằng?
Lời giải:
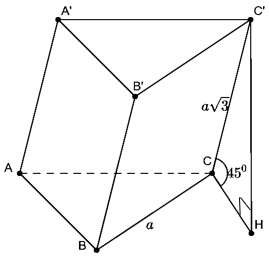
Gọi hình chiếu vuông góc của C’ xuông (ABC) là H.
Khi đó :
Diện tích tam giác ABC là
Suy ra thể tích lăng trụ là :
Câu 14. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ xuống (ABC) là trung điểm H của AB. Mặt bên (ACC’A’) tạo với đáy góc Tính thể tích khối lăng trụ ABC.A’B’C’
Lời giải:
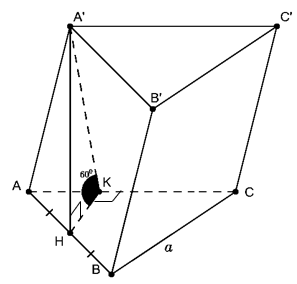
Trong (ABC) kẻ
Ta có:
Khi đó góc giữa (ABC) và (ACC’A’) là góc giữa HK và A’K là
Xét tam giác AHK vuông tại K có ,
Xét tam giác A’HK vuông tại H có
Diện tích tam giác ABC là
Suy ra thể tích lăng trụ là :
2. Bài tập tự luyện có hướng dẫn
Bài 1: Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, biết BA = BC = 2a, và (A’BC) hợp với đáy một góc 30°. Tính thể tích khối lăng trụ ABC.A’B’C’ là:
Lời giải:
Đáp án : D
Giải thích :
Khi đó:
Bài 2: Tính thể tích V của khối lập phương ABCD.A’B’C’D’, biết AC'=a√3
Lời giải:
Đáp án : A
Giải thích :
Gọi x là độ dài cạnh của hình lập phương
Xét tam giác AA’C vuông tại A có:
Do đó, thể tích của khối lập phương là V=a^3.
Bài 3: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60°, cạnh AB = a. Thể tích khối đa diện ABCC’ là:
Lời giải:
Đáp án : D
Giải thích :
Hình lăng trụ tam giác đều ABC.A’B’C’ ⇒ AA' ⊥ (ABC) và ∆ABC đều.
Gọi M là trung điểm của BC, do ∆ABC đều cạnh a nên:
Xét tam giác A’AM vuông tại A có:
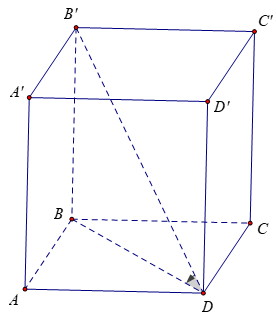
Bài 4: Cho lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với AB = 2a, AD = a và đường chéo B’D của lăng trụ hợp với đáy (ABCD) một góc 30°. Thể tích khối lăng trụ ABCD.A’B’C’D’ là:
Lời giải:
Đáp án : B
Giải thích :
BB' ⊥ (ABCD) nên BD là hình chiếu của B’D lên (ABCD)
Do B’D hợp với đáy ABCD một góc 30º nên ta có:
Xét tam giác B’BD vuông tại B có:
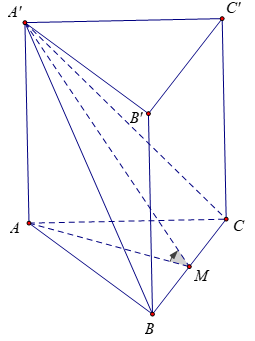
Bài 5: Cho khối lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, mặt phẳng (A’BC) hợp với đáy một góc 45°. Tính thể tích khối lăng trụ ABC.A’B’C’ là:
Lời giải:
Đáp án : A
Giải thích :
do ABC.A’B’C’ là lăng trụ đều nên A'A ⊥ (ABC), ∆ABC đều cạnh
Gọi M là trung điểm của BC, khi đó AM ⊥ BC
Mặt khác A'A ⊥ BC nên BC ⊥ (A' AM) ⇒ AM ⊥ BC
Xét tam giác A’AM vuông tại A có:
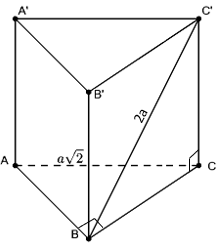
Bài 6: Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, cạnh BC=a√2, A’C tạo với đáy một góc 60°. Thể tích khối lăng trụ ABC.A’B’C’ là:
Lời giải:
Đáp án : C
Giải thích :
ABC là tam giác vuông cân tại A, cạnh BC=a√2
⇒ AB=AC=BC/√2=a
AA' ⊥ (ABC) nên AC là hình chiếu vuông góc của A’C lên (ABC)
⇒ (A' C;(ABC))= ∠(A'CA)=60°
Xét tam giác A’AC vuông tại A có:
Bài 7: Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều. Mặt phẳng (A’BC) tạo với đáy một góc 30° và diện tích tam giác A’BC bằng 8. Tính thể tích lăng trụ.
Lời giải:
Đáp án : B
Giải thích :
ABC.A’B’C’ là lăng trụ đứng nên A'A ⊥ (ABC),
Giả sử ∆ABC đều cạnh a
Gọi M là trung điểm của BC, khi đó AM ⊥ BC;AM=(a√3)/2
Mặt khác A'A ⊥ BC nên BC ⊥ (A' AM) ⇒ AM ⊥ BC
Xét tam giác A’AM vuông tại A có:
Bài 8: Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng a là:
Lời giải:
Đáp án : C
Giải thích :
Đáy A’B’C’ là tam giác đều cạnh a nên S(A' BC) = (a2 √3)/4
Khối lăng trụ đứng tam giác đều có tất cả các cạnh đều bằng a nên chiều cao
AA’ = a
Bài 9: Cho hình lăng trụ đứng ABC.A’B’C’ có AC = a, BC = 2a, ∠(ACB)=120º và đường thẳng A’C tạo với mặt phẳng (ABB’A’) góc 30°. Thể tích khối lăng trụ ABC.A’B’C’ là:
Lời giải:
Đáp án : B
Giải thích :
Kẻ CP ⊥ AB (P ∈ (AB).
Ta có:
⇒ Hình chiếu vuông góc của CA’ trên mặt phẳng (ABB’A’) là CP
Mà
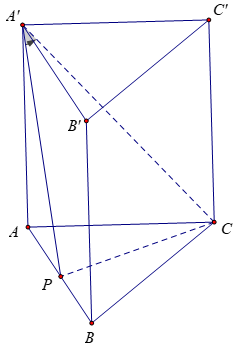
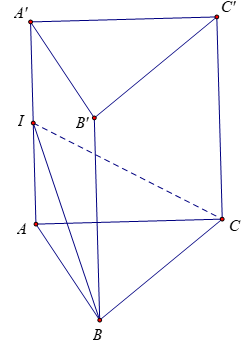
Bài 10: Cho hình lăng trụ đứng ABC.A’B’C’ có AA’ = a. Tam giác ABC đều cạnh a. Gọi I là trung điểm của AA’. Tìm mệnh đề đúng.
Lời giải:
Đáp án : C
Giải thích :
Ta có:
Xem thêm các dạng bài tập liên quan khác:
60 Bài tập về khối đa diện lồi và khối đa diện đều ( có đáp án năm 2023 )
60 Bài tập về mặt cầu (có đáp án năm 2023)
60 Bài tập khái niệm về mặt tròn xoay (có đáp án năm 2023)
60 Bài tập về phương trình mặt phẳng (có đáp án năm 2023)
60 Bài tập về phương trình đường thẳng trong không gian (có đáp án năm 2023)