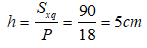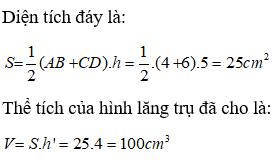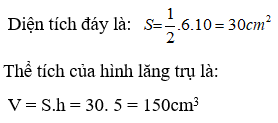60 Bài tập về diện tích xung quanh của hình lăng trụ. Thể tích của hình lăng trụ (có đáp án năm 2024)

Bài giảng Toán 8 Bài 5: Diện tích xung quanh của hình lăng trụ

Bài giảng Toán 8 Bài 6: Thể tích của hình lăng trụ

Kiến thức cần nhớ

1. Công thức tính diện tích xung quanh

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao:

S_xq = 2p.h    (p: nửa chu vi đáy, h: chiều cao)

Diện tích toàn phần của hình lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.

S_tp = S_xq + S_2day     

Ví dụ 1. Cho hình lăng trụ đứng có đáy là lục giác đều cạnh 6cm, chiều cao lăng trụ là 4cm. Tính diện tích xung quanh của hình lăng trụ?

Lời giải:

Do đáy của hình lăng trụ là lục giác đều cạnh 6cm nên chu  vi đáy là:

P = 6. 6 = 36cm

Diện tích xung quanh của hình lăng trụ là; 

S_xq = P.  h = 36.4 = 144 cm²

2. Công thức tính thể tích.

Thể tích của hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao:

V = S.h (S: diện tích đáy, h: chiều cao)

3. Ví dụ

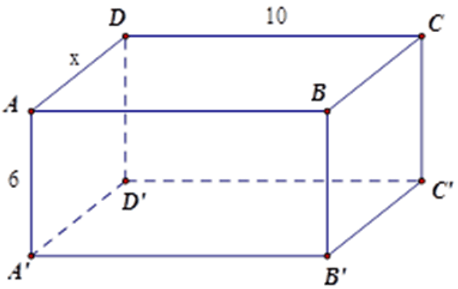
Cho hình lăng trụ đứng ABCD. A’B’C’D’ có đáy là hình thang vuông tại A và D.

Tính thể tích của hình lăng trụ biết AB = 6cm; CD = 4 cm; AD = 5cm và AA’ = 6cm

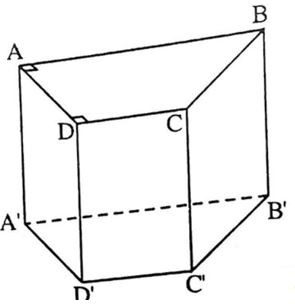
Lời giải:

Diện tích hình thang ABCD là:

$\mathrm{S}=\frac{1}{2}\left(\mathrm{AB}+\mathrm{CD}\right).\mathrm{AD}=\frac{1}{2}\left(6+4\right).5=25{\mathrm{cm}}^2$

Thể tích của hình lăng trụ là

V = S. AA’ = 25. 6 = 150 cm³.

Bài tập tự luyện

1. Bài tập vận dụng

Bài 1. Cho hình lăng trụ đứng ABCD.MNPQ có đáy ABCD là hình chữ nhật, AB = 6cm; BC = 4cm, chiều cao h = 3cm. Diện tích xung quanh và diện tích toàn phần của hình lăng trụ đứng là?

Lời giải:

Ta có nửa chu vi của đáy là:

p = AB + BC = 6 + 4 = 10 cm

Diện tích xung quanh của hình lăng trụ đứng là:

S_xq = 2ph = 2. 10.3 = 60cm²

Diện tích 1 đáy là: S = AB. BC =6.4 = 24 cm²

Diện tích toàn phần của hình lăng trụ đứng là:

S_tp = 60 + 2.24 = 108 cm²

Bài 2. Cho hình lăng trụ đứng đáy là tam giác có độ dài ba cạnh đáy là 4 cm, 6cm  và  8cm. Biết diện tích xung quanh bằng 90cm². Tính chiều cao của hình lăng trụ?

Lời giải:

Chu vi đáy là:  P = 4 + 6+ 8 = 18cm

Diện tích xung quanh của hình lăng trụ đứng

S_xq = P.h nên chiều cao:

$\mathrm{h}=\frac{{\mathrm{S}}_{\mathrm{xq}}}{\mathrm{P}}=\frac{90}{18}=5\mathrm{cm}$

Vậy chiều cao của hình trụ là 5cm.

Bài 3. Tính chiều cao của hình lăng trụ đứng ABCD.EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm; BD = 24cm và diện tích toàn phần bằng 1280 cm²

Lời giải:

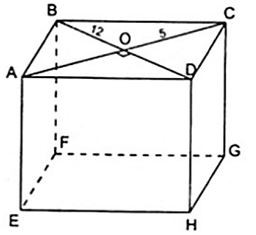
Diện  tích 1 đáy của hình lăng trụ là:

$\mathrm{S}=\frac{1}{2}\mathrm{AC}.\mathrm{BD}=120{\mathrm{cm}}^2$cm²

Mà S_tp = S_xq + S_2day

Nên diện tích xung quanh của hình lăng trụ là:

S_xq = S_tp – S_2day = 1280 – 2.120 = 1040 cm²

Vì đáy ABCD là hình thoi nên AC vuông góc với BD tại trung điểm O (tính chất về đường chéo của hình thoi).

Ta có $\mathrm{BO}=\frac{1}{2}\mathrm{BD}=12\mathrm{cm}; \mathrm{OC}=\frac{1}{2}\mathrm{AC}=5\mathrm{cm}$.

Áp dụng định lý Py – ta – go vào tam giác BOC vuông tại O ta được:

BC² = BO² + OC² = 12² + 5² = 169 nên BC = 13cm

Chu vi đáy là P = 4.13 = 52cm

Áp dụng công thức

${\mathrm{S}}_{\mathrm{xq}}=2\mathrm{p}.\mathrm{h}\Rightarrow \mathrm{h}=\frac{{\mathrm{S}}_{\mathrm{xq}}}{2\mathrm{p}}=\frac{1040}{52}=20\left(\mathrm{cm}\right)$

Chiều cao của hình đã cho là 20 cm.

Bài 4. Cho hình lăng trụ đứng ABC.MNP có đáy là tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Hình lăng trụ có chiều cao h = 4cm. Thể tích của hình lăng trụ đó là?

Lời giải:

Ta có diện tích đáy ABC là:

${\mathrm{S}}_{\mathrm{ABC}}=\frac{1}{2}\mathrm{AB}.\mathrm{AC}=\frac{1}{2}.6.8=24\left({\mathrm{cm}}^2\right)$

Thể tích của hình lăng trụ đó là:

$\mathrm{V}={\mathrm{S}}_{\mathrm{ABC}}.\mathrm{h}=24.4=96{\mathrm{cm}}^3$

Vậy thể tích của hình lăng trụ là 96 cm³.

Bài 5. Cho hình lăng trụ đứng ABCD.MNPQ có đáy hình thang AB// CD  và AB = 6cm;  CD = 10 cm và chiều cao của hình  thang là 4cm, chiều cao của hình lăng trụ là:  4cm.  Tính thể tích của hình lăng trụ?

Lời giải:

Diện tích đáy là:

$\mathrm{S}=\frac{1}{2}\left(\mathrm{AB}+\mathrm{CD}\right).\mathrm{h}=\frac{1}{2}.\left(6+10\right).4=32{\mathrm{cm}}^2$

Thể tích của hình lăng trụ đã cho là:

V = S.h’ = 32. 4 = 128 cm³

Vậy thể tích của hình lăng trụ là 128 cm³.

Bài 6. Một hình lăng trụ có kích thước như hình bên. Tính thể tích của hình lăng trụ.

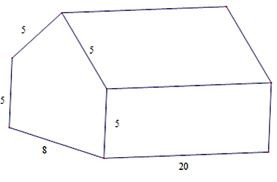
Lời giải:

Lăng trụ đã cho gồm một hình hộp chữ nhật AA’C’C. MNPQ và một lăng trụ tam giác ABC.A’B’C’ có cùng chiều cao.

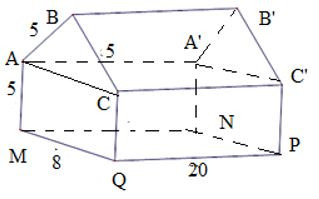
Thể tích hình hộp chữ nhật AA’C’C. MNPQ là:

V₁ = 5.8.20 = 800

Ta tính thể tích hình lăng trụ đứng tam giác ABC.A’B’C’:

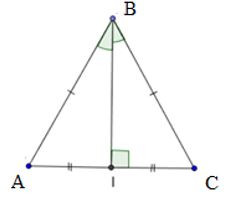
Ta có: AB = BC = 5; AC = 8.

Gọi I là trung điểm của AC là AI = IC = 4.

Áp dụng định lí Py ta go vào tam giác vuông BCI có:

BI² = BC² – CI² = 5² – 4² = 9 nên BI = 3

Diện tích tam giác ABC là $\mathrm{S}=\frac{1}{2}.\mathrm{BI}.\mathrm{AC}=\frac{1}{2}.3.8=12$

Thể tích hình lăng trụ đứng tam giác là:

 V₂ = 12 . 20 = 240

Thể tích của hình lăng trụ đã cho là:

V = 800 + 240 = 1040

Bài 7. Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A có AB = 3cm, AC = 4cm. Hình lăng trụ có chiều cao h = 3cm. Thể tích của hình lăng trụ đó là?

   A. V = 9( cm³ )        B. V = 18( cm³ )

   C. V = 24( cm³ )      D. V = 36( cm³ )

Lời giải:

Ta có: S_ABC = 1/2AB.AC = 1/2.3.4 = 6( cm² )

Khi đó: V = h.S_ABC = 3.6 = 18( cm³ )

Chọn đáp án B.

Bài 8. Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích xung quanh của hình lăng trụ đứng là?

   A. S_xq = 22,5( cm² )   B. S_xq = 45( cm² )

   C. S_xq = 30( cm² )     D. S_xq = 36( cm² )

Lời giải:

Ta có chu vi của đáy là: p = 2( AB + BC ) = 2( 4 + 5 ) = 18( cm )

Khi đó: S_xq = p.h = 18.2,5 = 45( cm² )

Chọn đáp án B.

Bài 9. Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích toàn phần của hình lăng trụ đứng là?

   A. S_tp = 62,5( cm² )   B. S_xq = 85( cm² )

   C. S_tp = 70( cm² )   D. S_xq = 76( cm² )

Lời giải:

Theo câu 2, ta có: S_xq = 45( cm² )

Khi đó ta có: S_tp = S_xq + 2S = 45 + 2.4.5 = 85( cm² )

Chọn đáp án B.

Bài 10. Cho hình lăng trụ đứng tam giác có độ dài ba cạnh đáy là 4 cm, 6cm và 8cm. Biết diện tích xung quanh bằng 90cm². Tính chiều cao của hình lăng trụ?

   A. 5cm     B. 6cm

   C. 4cm     D. 8cm

Lời giải:

Chu vi đáy là: P = 4 + 6 + 8 = 18cm

Diện tích xung quanh của hình lăng trụ đứng

S_xq = P.h nên chiều cao:

Chọn đáp án A

Bài 11. Cho hình lăng trụ đứng ABCD.MNPQ có đáy hình thang AB// CD và AB = 4cm; CD = 6cm và chiều cao của hình thang là 5cm, chiều cao của hình lăng trụ là: 4cm. Tính thể tích của hình lăng trụ?

   A. 125cm³     B. 120cm³

   C. 100cm³     D. Đáp án khác

Lời giải:

Chọn đáp án C

Bài 12. Cho hình lăng trụ đứng có đáy là lục giác đều cạnh 6cm, chiều cao lăng trụ là 6cm. Tính diện tích xung quanh của hình lăng trụ?

   A. 160cm²     B. 216cm²

   C. 250cm²     D. 320cm²

Lời giải:

Do đáy của hình lăng trụ là lục giác đều cạnh 6cm nên chu vi đáy là:

P = 6.6 = 36cm

Diện tích xung quanh của hình lăng trụ là:

S_xq = P.h = 36.6 = 216 cm²

Chọn đáp án B

Bài 13. Cho hình lăng trụ đứng có đáy là hình thoi. Độ dài hai đường chéo là 6cm và 10cm. Biết chiều cao của hình lăng trụ là 5cm. Tính thể tích của hình lăng trụ?

   A. 100cm³     B. 150cm³

   C. 200cm³     D. 180cm³

Lời giải:

Chọn đáp án B

Bài 14. Cho hình lăng trụ đứng ABC.A’B’C’, AB = 6cm; AC = 8cm, AA’ = 5cm và diện tích xung quanh là 120cm². Hỏi tam giác ABC là tam giác gì

   A. Tam giác cân

   B. Tam giác nhọn

   C.Tam giác tù

   D. Tam giác vuông

Lời giải:

Chọn đáp án D

Bài 12. Cho hình lăng trụ đứng ABCD.MNPQ có đáy ABCD là hình bình hành có AB = 6cm, BC = 4cm , AM = 5cm. Tính diện tích xung quanh của hình lăng trụ?

   A. 100cm²     B. 120cm²

   C. 150cm²     D. 200cm²

Lời giải:

Chu vi đáy là:

P = 2(AB + BC) = 2.(6 + 4) = 20cm

Diện tích xung quanh của hình lăng trụ đã cho là:

S_xq = S_d . h = 20. 5 = 100cm²

Chọn đáp án A

Bài 15: Một hình hộp chữ nhật có kích thước của đáy là 10 cm và 15 cm. Biết diện tích xug quang bằng tổng diện tích hai đáy. Độ dài chiều cao là:

A. 12 cm        

B. 6 cm           

C. 8 cm           

D. 10 cm

Lời giải

Đặt AA' = x.

Diện tích xung quang bằng:

2 (10 + 15).x = 50x (cm²)

Tổng diện tích hai đáy bằng 2.10.15 = 300 (cm²)

Ta có 50x = 300 ⇔  x = 6

Vậy chiều cao bằng 6 cm.

Đáp án cần chọn là: B

Bài 16: Cho hình lăng trụ tam giác đều ABC. A'B'C' có chiều cao bằng 2 cm, 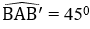. Tính diện tích xung quang của hình lăng trụ.

A. 15 cm²       

B. 6 cm²            

C. 12 cm²       

D. 16 cm²

Lời giải

Tam giác vuông ABB' có 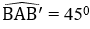 nên là tam giác vuông cân tại B nên AB = BB' = 2 cm.

Vì tam giác ABC đều nên chu vi bằng 3AB = 3.2 = 6 cm

Diện tích xung quanh bằng 6.2 = 12 (cm²)

Đáp án cần chọn là: C

Bài 17: Cho hình lăng trụ tam giác đều ABC. A'B'C' có chiều cao bằng 2 cm, . Tính diện tích xung quang của hình lăng trụ.

A. 15 cm²       

B. 6 cm²            

C. 12 cm²       

D. 16 cm²

Lời giải

Tam giác vuông ABB' có 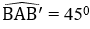 nên là tam giác vuông cân tại B nên AB = BB' = 2 cm.

Vì tam giác ABC đều nên chu vi bằng 3AB = 3.2 = 6 cm

Diện tích xung quanh bằng 6.2 = 12 (cm²)

Đáp án cần chọn là: C

Bài 18: Một hình hộp chữ nhật có diện tích xung quanh bằng 120 cm², chiều cao bằng 6cm. Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.

A. 8 cm          

B. 7 cm              

C. 6 cm           

D. 5 cm

Lời giải

Gọi a và b là các kích thước của đáy.

Ta có V = 6ab nên V lớn nhât ⇔ ab lớn nhất

S_xq = 120 nên 2 (a+b).6 = 120 hay a + b = 10

Ta có:

ab = a (10 – a) = -a² +10a = -(a – 5)² + 25 ≤ 25

Suy ra V = 6ab ≤ 6.25 = 150.

Thể tích lớn nhất bằng 150 cm³ khi a = b = 5, tức là các cạnh đáy bằng 5 cm.

Đáp án cần chọn là: D

Bài 19: Một hình hộp chữ nhật có diện tích xung quanh bằng 100 cm², chiều cao bằng 5cm. Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.

A. 8 cm          

B. 7 cm              

C. 6 cm           

D. 5 cm

Lời giải

Gọi a và b là các kích thước của đáy.

Ta có V = 5ab nên V lớn nhât ⇔ ab lớn nhất

S_xq = 100 nên 2 (a+b).5 = 120 hay a + b = 10

Ta có:

ab = a (10 – a) = -a² +10a = -(a – 5)² + 25 ≤ 25

Suy ra V = 5ab ≤ 5.25 = 125.

Thể tích lớn nhất bằng 125 cm³ khi a = b = 5, tức là các cạnh đáy bằng 5 cm.

Đáp án cần chọn là: D

2. Bài tập tự luyện có hướng dẫn

(Xem trong file đính kèm bên dưới)

Xem thêm các dạng bài tập liên quan khác:

60 Bài tập về hình lăng trụ đứng (có đáp án năm 2024)

60 Bài tập về diện tích xung quanh của hình lăng trụ. Thể tích của hình lăng trụ (có đáp án năm 2024)

300 Bài tập Toán 8 chương 4: Hình lăng trụ đứng. Hình chóp đều (có đáp án năm 2024)

70 Bài tập Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác (có đáp án năm 2024)

Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác