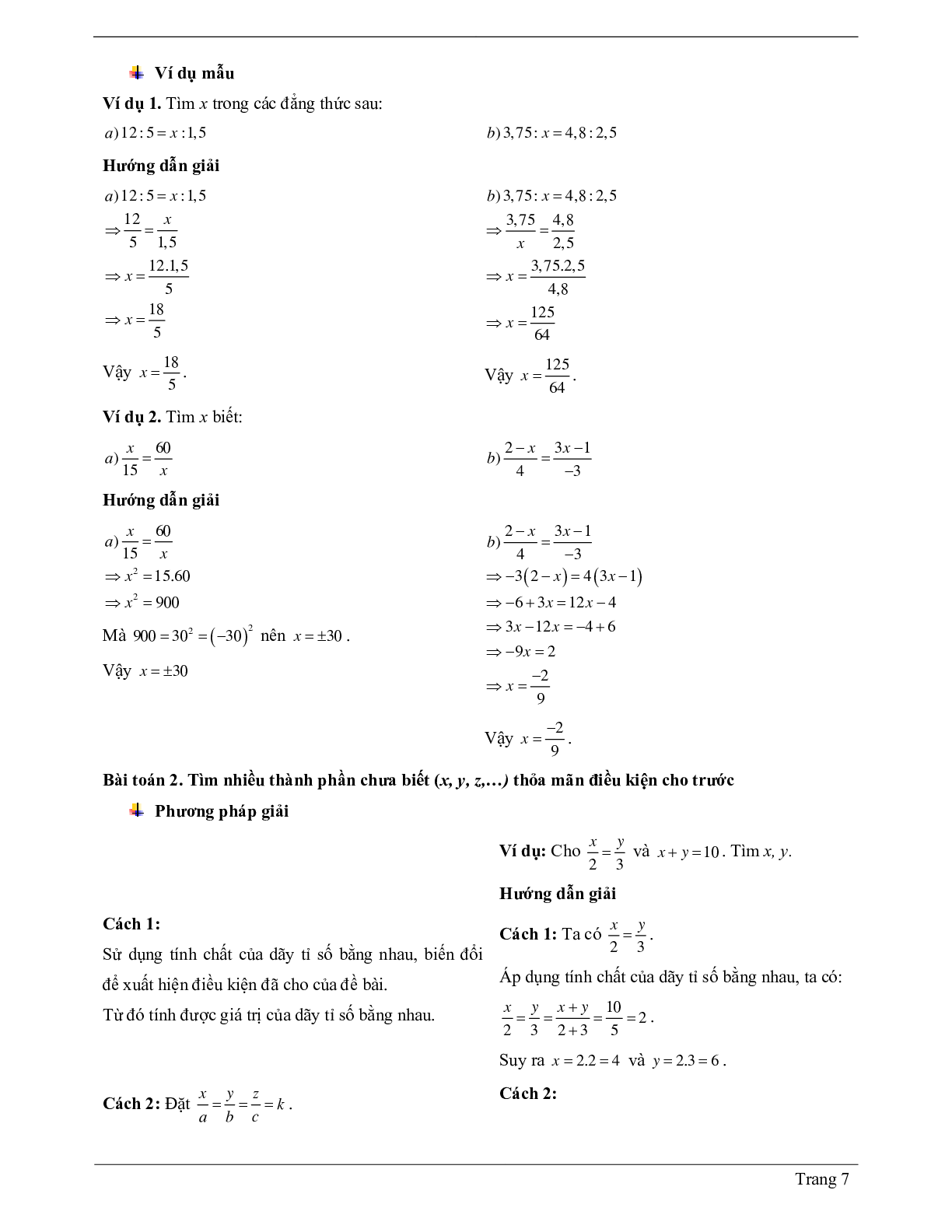60 Bài tập về dãy tỉ số bằng nhau (có đáp án năm 2024) - Toán 7

Bài tập về dãy tỉ số bằng nhau

Kiến thức cần nhớ

1. Khái niệm

Những tỉ số bằng nhau và được viết nối với nhau bởi các dấu đẳng thức tạo thành dãy tỉ số bằng nhau.

Chú ý:

- Với dãy tỉ số bằng nhau $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{e}}{\mathrm{g}}$ ta cũng viết a : b = c : d = e : g.

- Khi có dãy tỉ số bằng nhau $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{e}}{\mathrm{g}}$, ta nói các số a, c, e tỉ lệ với các số b, d, g và viết là a : c : e = b : d : g.

Ví dụ:

- Dãy tỉ số bằng nhau $\frac{1}{4}=\frac{-9}{-36}=\frac{8}{32}$.

- Khi nói ba số x ; y ; z tỉ lệ với các số 2 ; 3 ; 4 thì x : y : z = 2 : 3 : 4 và ta viết được dãy tỉ số bằng nhau: $\frac{\mathrm{x}}{2}=\frac{\mathrm{y}}{3}=\frac{\mathrm{z}}{4}$.

2. Tính chất

Từ tỉ lệ thức $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}$, ta suy ra:

$\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{a}+\mathrm{c}}{\mathrm{b}+\mathrm{d}}=\frac{\mathrm{a}-\mathrm{c}}{\mathrm{b}-\mathrm{d}}$( b ≠ d và b ≠ –d).

Nhận xét: Tính chất trên còn mở rộng cho dãy tỉ số bằng nhau. Chẳng hạn từ dãy tỉ số bằng nhau  $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{e}}{\mathrm{g}}$, ta suy ra:

$\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{e}}{\mathrm{g}}=\frac{\mathrm{a}+\mathrm{c}+\mathrm{e}}{\mathrm{b}+\mathrm{d}+\mathrm{g}}=\frac{\mathrm{a}-\mathrm{c}+\mathrm{e}}{\mathrm{b}-\mathrm{d}+\mathrm{g}}$  (giả thiết các tỉ số đều có nghĩa).

Ví dụ: Từ dãy tỉ số $\frac{1}{3}=\frac{0,15}{0,45}=\frac{6}{18}$, áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{1}{3}=\frac{0,15}{0,45}=\frac{6}{18}=\frac{1+0,15+6}{3+0,45+18}=\frac{7,15}{21,45}$.

3. Ứng dụng

Các tính chất của dãy tỉ số bằng nhau có nhiều ứng dụng trong thực tiễn, chẳng hạn, ứng dụng vào bài toán chia đại lượng cho trước thành các phần theo tỉ lệ cho trước.

Ví dụ: Số viên bi của ba bạn Minh, Hùng, Dũng tỉ lệ với các số 2 ; 4 ; 5. Tính số viên bi của mỗi bạn, biết rằng ba bạn có tất cả 44 viên bi.

Hướng dẫn giải

Gọi số viên bi của ba bạn Minh, Hùng, Dũng lần lượt là x (viên bi) ; y (viên bi) ; z (viên bi).

Ta có :  $\frac{\mathrm{x}}{2}=\frac{\mathrm{y}}{4}=\frac{\mathrm{z}}{5}$ và x + y + z = 44.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{\mathrm{x}}{2}=\frac{\mathrm{y}}{4}=\frac{\mathrm{z}}{5}=\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{2+4+5}=\frac{44}{11}=4$

Suy ra  x = 2.4 = 8 ; y = 4.4 = 16 ; z = 5.4 = 20.

Vậy Minh có 8 viên bi, Hùng có 16 viên bi, Dũng có 20 viên bi.

Các dạng bài tập về dãy tỉ số bằng nhau

Dạng 1: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên.

1. Phương pháp giải:

- Viết các số hữu tỉ dưới dạng phân số.

- Thực hiện phép chia phân số.

2. Ví dụ minh họa:

Ví dụ 1: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên:

2,05 : 1,2

Giải:

Ta có: 2,05 : 1,2 = $\frac{41}{20}:\frac{6}{5}=\frac{41}{20}.\frac{5}{6}=\frac{41}{24}$

Vậy tỉ số giữa hai số hữu tỉ 2,05 : 1,2 bằng tỉ số giữa hai số nguyên 41: 24

Dạng 2: Tìm hai số biết tổng (hoặc hiệu) và tỉ số của chúng.

1. Phương pháp giải:

Để tìm hai số x và y biết tổng x + y = s hoặc hiệu x – y = d và tỉ số $\frac{x}{y}=\frac{a}{b}$  

ta làm như sau $\frac{x}{y}=\frac{a}{b}$ => $\frac{x}{a}=\frac{y}{b}$

Áp dụng tính chất của dãy tỉ số bằng nhau:

2. Ví dụ minh họa:

Ví dụ 2: Tìm x, y biết:

a) x + y =60 và $\frac{x}{9}=\frac{y}{11}$

b) y – x = 24 và $\frac{x}{4}=\frac{y}{7}$

Giải:

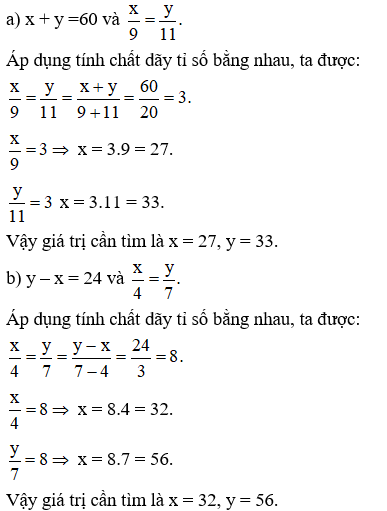
Dạng 6: Chia một số thành các phần tỉ lệ với các số cho trước.

1. Phương pháp giải:

Giả sử phải chia số S thành ba phần x, y, z tỉ lệ với các số a, b, c. Ta làm như sau: $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=\frac{x+y+z}{a+b+c}=\frac{S}{a+b+c}$

Do đó,

2. Ví dụ minh họa:

Ví dụ 4: Các cạnh của một tam giác có độ dài tỉ lệ với các số 3; 5; 7. Tính độ dài mỗi cạnh của tam giác, biết chu vi của nó bằng 40,5 cm.

Giải:

Gọi độ dài các cạnh của tam giác lần lượt là a, b, c (cm, 0 < a, b, c < 40,5).

Vậy độ dài ba cạnh của tam giác lần lượt là 8,1 cm; 13,5 cm; 18,9 cm.

Dạng 5: Tìm hai số biết tích và tỉ số của chúng.

1. Phương pháp giải:

Giả sử phải tìm hai số x, y biết x.y = P và $\frac{x}{y}=\frac{a}{b}$

Đặt $\frac{x}{a}=\frac{y}{a}=k$  , ta có x = k.a, y = k.b.

Do đó x.y = (k.a).(k.b) = k².ab = P => $k^2=\frac{P}{ab}$

Từ đó tìm được k rồi suy ra x và y.

2. Ví dụ minh họa:

Ví dụ 5: Tìm hai số x và y, biết rằng:

$\frac{x}{3}=\frac{y}{4}$ và xy = 48.

Giải:

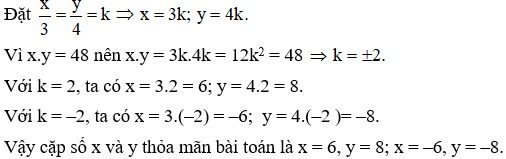
Dạng 6: Chứng minh đẳng thức từ một tỉ lệ thức cho trước.

1. Phương pháp giải:

Cho tỷ lệ thức $\frac{a}{b}=\frac{c}{d}$ Cần chứng minh tỷ lệ thức $\frac{x}{y}=\frac{m}{n}$ theo k, ta thường làm các phương pháp sau:

Phương pháp 1. Chứng tỏ rằng: ad = bc.

Phương pháp 2: Đặt k là giá trị chung của $\frac{a}{b};\frac{c}{d}$ Tính $\frac{x}{y};\frac{m}{n}$  theo k.

Phương pháp 3: Dùng biến đổi đại số và tính chất của dãy tỷ số bằng nhau để từ tỷ lệ thức đã cho biến đổi dần thành tỷ lệ thức phải chứng minh.

2. Ví dụ minh họa:

Ví dụ 6: Cho a, b, c, d khác 0 từ tỷ lệ thức: $\frac{a}{b}=\frac{c}{d}$ Chứng minh:

a)$\frac{a-b}{a}=\frac{c-d}{c}$

b)${\left(\frac{a-b}{c-d}\right)}^2=\frac{ab}{cd}$

Giải:

Bài tập (có đáp án)

1. Bài tập vận dụng

A. Bài tập tự luận

Bài 1. Tìm hai số x và y, biết : $\frac{\mathrm{x}}{4}=\frac{\mathrm{y}}{7}$ và x + y = 99.

Hướng dẫn giải

Áp dụng tính chất dãy tỉ số bằng nhau ta có:  $\frac{\mathrm{x}}{4}=\frac{\mathrm{y}}{7}=\frac{\mathrm{x}+\mathrm{y}}{4+7}=\frac{99}{11}=9$.

Vậy  x = 4 . 9 = 36;  y = 7 . 9 = 63.

Bài 2.  Một mảnh vườn hình chữ nhật với tỉ số giữa độ dài hai cạnh của nó bằng 3 : 5 và chu vi bằng 48 m. Tính diện tích mảnh vườn đó.

Hướng dẫn giải

Gọi độ dài hai cạnh của mảnh vườn hình chữ nhật lần lượt là a (mét) và b (mét).

Ta có $\frac{\mathrm{a}}{3}=\frac{\mathrm{b}}{5}$ và 2.(a + b) =  48 (chu vi hình chữ nhật bằng 48 m) nên a + b = 24.

Áp dụng tính chất dãy tỉ số bằng nhau ta có: $\frac{\mathrm{a}}{3}=\frac{\mathrm{b}}{5}=\frac{\mathrm{a}+\mathrm{b}}{3+5}=\frac{24}{8}=3$.

Suy ra a = 3.3 = 9 ;  b = 5 . 3 = 15.

Vậy diện tích của mảnh vườn là 9 . 15 = 135 (m²).

Bài 3. Tìm hai số a và b, biết : a : 2 = b : (–5)  và a – b = –7.

Hướng dẫn giải

Từ a : 2 = b : (–5)  ta có tỉ lệ thức $\frac{\mathrm{a}}{2}=\frac{\mathrm{b}}{-5}$.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:  $\frac{\mathrm{a}}{2}=\frac{\mathrm{b}}{-5}=\frac{\mathrm{a}-\mathrm{b}}{2-(-5)}=\frac{-7}{7}=-1$.

Vậy  a = 2. (–1) = –2 ;  b = (–5). (–1) = 5.

B. Bài tập trắc nghiệm

Câu 1. Cho $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{5}$ và x + y = 24. Giá trị của 3x + 5y là:

A. 132;

B. 80;

C. 102;

D. 78.

Hướng dẫn giải

Đáp án đúng là: C.

Từ tỉ lệ thức $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{5}$ và x + y = 24 áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{5}=\frac{\mathrm{x}+\mathrm{y}}{3+5}=\frac{24}{8}=3.$

Suy ra:

+) $\frac{\mathrm{x}}{3}=3$ do đó x = 3.3 = 9;

+) $\frac{\mathrm{y}}{5}=3$ do đó y = 3.5 = 15.

Khi đó 3x + 5y = 3.9 + 5.15 = 102.

Vậy 3x + 5y = 102.

Câu 2. Khẳng định nào sau đây là đúng?

A. $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{5}=\frac{2\mathrm{x}+3\mathrm{y}}{15};$ 

B. $\frac{\mathrm{x}}{4}=\frac{\mathrm{y}}{5}=\frac{2\mathrm{x}+4\mathrm{y}}{28};$ 

C. $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{7}=\frac{\mathrm{x}+3\mathrm{y}}{25};$ 

D. $\frac{\mathrm{x}}{5}=\frac{\mathrm{y}}{6}=\frac{2\mathrm{x}+\mathrm{y}}{15}.$ 

Hướng dẫn giải

Đáp án đúng là: B.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

+) $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{5}=\frac{2\mathrm{x}}{6}=\frac{3\mathrm{y}}{15}=\frac{2\mathrm{x}+3\mathrm{y}}{6+15}=\frac{2\mathrm{x}+3\mathrm{y}}{21}$. Do đó phương án A là sai.

+) $\frac{\mathrm{x}}{4}=\frac{\mathrm{y}}{5}=\frac{2\mathrm{x}}{8}=\frac{4\mathrm{y}}{20}=\frac{2\mathrm{x}+4\mathrm{y}}{8+20}=\frac{2\mathrm{x}+4\mathrm{y}}{28}.$ Do đó phương án B là đúng.

+) $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{7}=\frac{3\mathrm{y}}{21}=\frac{\mathrm{x}+3\mathrm{y}}{3+21}=\frac{\mathrm{x}+3\mathrm{y}}{24}.$ Do đó phương án C là sai.

+) $\frac{\mathrm{x}}{5}=\frac{\mathrm{y}}{6}=\frac{2\mathrm{x}}{10}=\frac{2\mathrm{x}+\mathrm{y}}{10+6}=\frac{2\mathrm{x}+\mathrm{y}}{16}.$ Do đó phương án D là sai.

Câu 3. Một hình chữ nhật có chu vi 50 cm, tỉ số giữa hai cạnh bằng $\frac{3}{2}$ thì diện tích của hình chữ nhật là:

A. 150 cm²;

B. 200 cm²;

C. 250 cm²;

D. 300 cm².

Hướng dẫn giải

Đáp án đúng là: A.

Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là x, y (cm) (x, y > 0)

Tỉ số giữa hai cạnh bằng $\frac{3}{2}$ nên ta có $\frac{\mathrm{x}}{\mathrm{y}}=\frac{3}{2}$ suy ra $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{2}$ 

Nửa chu vi của hình chữ nhật là 50 : 2 = 25 (cm).

Khi đó x + y = 25.

Áp dụng tính chất dãy tỉ số bằng nhau ta có $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{2}=\frac{\mathrm{x}+\mathrm{y}}{3+2}=\frac{25}{5}=5$

Suy ra:

+) $\frac{\mathrm{x}}{3}=5$ do đó x = 3.5 = 15;

+) $\frac{\mathrm{y}}{2}=5$ do đó y = 5.2 = 10.

Vậy hình chữ nhật có chiều dài là 15 cm, chiều rộng là 10 cm.

Diện tích của hình chữ nhật là: 15 . 10 = 150 cm².

Vậy diện tích của hình chữ nhật là 150 cm².

2. Bài tập tự luyện có hướng dẫn (chuyên đề)

Xem thêm các dạng bài tập Toán khác :

70 Bài tập về đại lượng tỉ lệ nghịch (có đáp án năm 2023)

60 Bài tập về dãy tỉ số bằng nhau (có đáp án năm 2023)

60 Bài tập về tỉ lệ thức (có đáp án năm 2023)

60 Bài tập làm tròn số và ước lượng (có đáp án năm 2023)

60 Bài tập Tập hợp các số thực (có đáp án năm 2024)