70 Bài tập về đại lượng tỉ lệ nghịch (có đáp án năm 2024) - Toán 7

Bài tập về đại lượng tỉ lệ nghịch

Kiến thức cần nhớ

1. Khái niệm

- Nếu đại lượng y liên hệ với đại lượng x theo công thức $\mathrm{y}=\frac{\mathrm{a}}{\mathrm{x}}$ hay xy = a (với a là một hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.

- Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a thì x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ a. Ta nói x và y là hai đại lượng tỉ lệ nghịch với nhau.

Ví dụ: Nếu  $\mathrm{y}=\frac{-5}{\mathrm{x}}$ thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ –5. Khi đó x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ –5.

2. Tính chất

Nếu hai đại lượng tỉ lệ nghịch với nhau thì:

- Tích hai giá trị tương ứng của chúng luôn không đổi (bằng hệ số tỉ lệ).

- Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ lệ hai giá trị tương ứng của đại lượng kia.

Giả sử y tỉ lệ nghịch với x theo hệ số tỉ lệ a. Với mỗi giá trị x₁, x₂, x₃, … khác 0 của x, ta có một giá trị tương ứng y₁, y₂, y₃,… của y. Khi đó:

x₁ y₁  =  x₂ y₂ = x₃ y₃ = …= a hay $\frac{{\mathrm{x}}_1}{\frac{1}{{\mathrm{y}}_1}}=\frac{{\mathrm{x}}_2}{\frac{1}{{\mathrm{y}}_2}}=\frac{{\mathrm{x}}_3}{\frac{1}{{\mathrm{y}}_3}}=\mathrm{...}=\mathrm{a};$

$\frac{{\mathrm{x}}_1}{{\mathrm{x}}_2}=\frac{{\mathrm{y}}_2}{{\mathrm{y}}_1};\frac{{\mathrm{x}}_1}{{\mathrm{x}}_3}=\frac{{\mathrm{y}}_3}{{\mathrm{y}}_1};\mathrm{...}$

3. Một số bài toán

Chú ý:

- Năng suất lao động và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.

- Số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.

Bài toán 1: Cho biết 35 công nhân xây một ngôi nhà hết 168 ngày. Hỏi nếu chỉ có 28 công nhân xây ngôi nhà đó thì hết bao nhiêu ngày (giả sử năng suất làm việc của mỗi công nhân là như nhau).

Hướng dẫn giải

Gọi x (công nhân), y (ngày) lần lượt là số công nhân và thời gian xây xong ngôi nhà. Khi đó, mối quan hệ giữa số công nhân (x) và thời gian xây xong ngôi nhà (y) được cho bởi bảng:

Ta có thời gian xây xong nhà (y) tỉ lệ nghịch với số công nhân làm việc theo hệ số tỉ lệ

a =  x₁ .  y₁ = 35 . 168 = 5 880.

Suy ra 28 . y₂ = 5 880. Vì thế y₂ = 5 880 : 28 = 210 (ngày)

Vậy 28 công nhân xây xong ngôi nhà trong 210 ngày.

Bài toán 2: Để tổ chức liên hoan cho gia đình, bác Ngọc dự định mua 2,9 kg thực phẩm gồm: thịt bò, thịt lợn, tôm sú. Số tiền bác Ngọc mua mỗi loại thực phẩm là như nhau. Biết giá thịt bò là 280 nghìn đồng/kg, giá thịt lợn là 160 nghìn đồng/kg và tôm sú là 320 nghìn đồng/kg. Mỗi loại thực phẩm bác Ngọc mua được là bao nhiêu kg?

Hướng dẫn giải

Gọi x (kg), y (kg), z (kg) lần lượt là số lượng thịt bò, thịt lợn, tôm sú mà bác Ngọc mua được. Khi đó: x + y + z = 2,9.

Vì số tiền mua mỗi loại thực phẩm là như nhau nên 280 . x = 160 . y = 320 . z hay 7 . x  =  4 . y  =  8 . z             (chia đồng thời các vế cho 40).

Do đó : $\frac{\mathrm{x}}{\frac{1}{7}}=\frac{\mathrm{y}}{\frac{1}{4}}=\frac{\mathrm{z}}{\frac{1}{8}}$.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{\mathrm{x}}{\frac{1}{7}}=\frac{\mathrm{y}}{\frac{1}{4}}=\frac{\mathrm{z}}{\frac{1}{8}}=\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{\frac{1}{7}+\frac{1}{4}+\frac{1}{8}}=\frac{2,9}{\frac{29}{56}}=5,6$.

Do đó:

$\mathrm{x}=5,6\cdot \frac{1}{7}=0,8$ (kg).

$\mathrm{y}=5,6\cdot \frac{1}{4}=1,4$ (kg).

$\mathrm{z}=5,6\cdot \frac{1}{8}=0,7$ (kg).

Vậy Bác Ngọc mua 0,8 kg thịt bò, 1,4 kg thịt lợn và 0,7 kg tôm sú.

Các dạng bài tập đại lượng tỉ lệ nghịch

Dạng 1: Tính hệ số tỉ lệ, biểu diễn x theo y, tính một giá trị khi biết giá trị kia.

1. Phương pháp giải:

Áp dụng công thức $y=\frac{a}{x}$ để xác định tương quan tỉ lệ thuận giữa hai đại lượng và xác định hệ số tỉ lệ.

2. Ví dụ minh họa:

Ví dụ 1: Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau khi x = 6 thì y = 10.

a) Tìm hệ số tỉ lệ a của y đối với x;

b) Hãy biểu diễn y theo x;

c) Tính giá trị của y khi x = 4; x =12.

Giải:

Hai đại lượng x và y tỉ lệ nghịch với nhau theo số a nên ta có công thức $y=\frac{a}{x}$ hay x.y = a.

a) Với x = 6, y = 10 ta có a = 6.10 = 60.

 Vậy y và x tỉ lệ nghịch theo hệ số là 60.

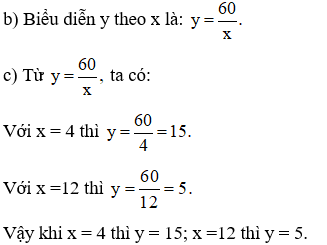
Dạng 2: Lập bảng giá trị tương ứng của hai đại lượng tỉ lệ nghịch.

1. Phương pháp giải:

- Xác định hệ số tỉ lệ a.

- Dùng công thức $y=\frac{a}{x}$ hay $x=\frac{a}{y}$ để tìm các giá trị tương ứng của x và y.

2. Ví dụ minh họa:

Ví dụ 2: Cho x và y là hai đại lượng tỉ lệ nghịch. Tìm công thức liên hệ giữa x và y và điền vào chỗ trống.

Giải:

Gọi hệ số tỉ lệ của x và y là a, nghĩa là $y=\frac{a}{x}$ hay x.y = a.

Ta có x = –15 thì y = –  4 nên suy ra a = x.y = (–15).(– 4) = 60.

Vậy x.y = 60.

Khi x = 20 thì y = 60 : 20 = 3.

Khi x = 4 thì y = 60 : 4 = 15

Khi x = – 0,5 thì y = 60 : (–0,5) = –120

Khi x = 6 thì y = 60 : 6 = 10

Khi y = 30 thì x = 60 : 30 = 2.

Khi x = –1,5 thì y = 60 : (–1,5) = – 40.

Vậy ta có bảng sau :

Dạng 3: Nhận biết hai đại lượng có tỉ lệ nghịch không.

1. Phương pháp giải:

Dựa vào định nghĩa và tính chất của hai đại lượng tỉ lệ nghịch.

Xét xem tất cả các tích các giá trị tương ứng của hai đại lượng có bằng nhau không.

2. Ví dụ minh họa:

Ví dụ 3: Các đại lượng x và y có tỉ lệ nghịch với nhau hay không nếu bảng các giá trị tương ứng của chúng như sau:

a)

b)

Giải:

a) Ta thấy: 10.6,75 = 15.4,5 = 22,5.3 = 37,5.1,8 = 67,5 ≠ 30.2,15 = 64,5.

Vậy x và y không phải là hai đại lượng tỉ lệ nghịch.

b) Ta thấy: 1.12 = (–2,4).(–5) = 4.3 = (– 6).(–2) = 8.1,5 = 12.

Vậy x và y là hai đại lượng tỉ lệ nghịch.

Dạng 4: Các bài toán về đại lượng tỉ lệ nghịch.

1. Phương pháp giải:

Bài toán 1: Toán về đại lượng tỉ lệ nghịch.

- Xác định tương quan tỉ lệ nghịch giữa hai đại lượng.

- Áp dụng tính chất về tỉ số các giá trị của hai đại lượng tỉ lệ nghịch.

Bài toán 2: Chia một số thành những phần tỉ lệ nghịch với các số cho trước.

Giả sử phải chia số M thành ba phần x, y, z tỉ lệ với các số a, b, c. Ta có

ax = by = cz  hay $\frac{x}{\frac{1}{a}}=\frac{y}{\frac{1}{b}}=\frac{z}{\frac{1}{c}}.$

Như vậy, để chia số M thành các phần tỉ lệ nghịch với a, b, c (khác 0), ta chỉ cần chia số M thành các phần tỉ lệ thuận với các số $\frac{1}{a},\frac{1}{b},\frac{1}{c}.$

Sau đó, áp dụng tính chất của dãy tỉ số bằng nhau để giải quyết bài toán.

2. Ví dụ minh họa:

Ví dụ 4: Để làm một công việc, người ta cần huy động 40 công nhân làm trong 12 giờ. Nếu số người tăng thêm 8 công nhân thì thời gian hoàn thành công việc là mấy giờ? (giả sử năng suất làm việc của mỗi người là như nhau).

Giải:

Vì năng suất làm việc của mỗi người là như nhau nên số công nhân và số giờ để hoàn thành công việc là hai đại lượng tỉ lệ nghịch.

Gọi số công nhân là y (công nhân); thời gian hoàn thành công việc sau khi đã bổ sung thêm người là x (giờ)

Ta có x.y = a

Khi y = 40 thì x = 12 nên ta có a = 40.12 = 480.

Do đó x.y = 480.

Số công nhân sau khi tăng thêm là: 40 + 8 = 48 (công nhân)

Vậy khi y = 48 thì x = 480 : 48 = 10.

Vậy sau khi tăng thêm 8 công nhân thì thời gian hoàn thành công việc là 10 giờ.

Ví dụ 5: Để đi từ A đến B có thể dùng máy bay, ô tô và xe lửa. Vận tốc của máy bay, ô tô và xe lửa tỉ lệ với 6; 2; 1. Biết thời gian đi từ A đến B bằng máy bay ít hơn so với đi bằng ô tô là 6 giờ. Hỏi thời gian máy bay, ô tô và xe lửa đi quãng đường AB là bao lâu?

Giải:

Gọi thời gian máy bay, ô tô và xe lửa đi từ A đến B lần lượt là a, b, c (giờ)

Theo đề bài ta có: b – a = 6.

Trên cùng một quãng đường AB thì thời gian tỉ lệ nghịch với vận tốc.

Do đó: 6a = 2b = c hay $\frac{a}{\frac{1}{6}}=\frac{b}{\frac{1}{2}}=\frac{c}{1}$  

Theo tính chất dãy tỉ số bằng nhau, ta có:

$\frac{a}{\frac{1}{6}}=\frac{b}{\frac{1}{2}}=\frac{c}{1}=\frac{b-a}{\frac{1}{2}-\frac{1}{6}}=\frac{6}{\frac{1}{3}}=18.$

Do đó: $a=18.\frac{1}{6}=3$

           $b=18.\frac{1}{2}=9$

          c = 18.1 = 18

Vậy thời gian máy bay, ô tô và xe lửa đi quãng đường AB lần lượt là 3 giờ, 9 giờ và 18 giờ.

Bài tập (có đáp án)

1. Bài tập vận dụng

A. Bài tập tự luận

Bài 1. Một ô tô dự định đi từ A đến B trong 6 giờ. Nhưng thực tế ô tô đi với vận tốc gấp $\frac{4}{3}$ vận tốc dự định. Tính thời gian ô tô đã đi.

Hướng dẫn giải

Gọi t (h) là thời gian thực tế ô tô đã đi.

Vì vận tốc thực tế ô tô đi gấp  $\frac{4}{3}$ vận tốc dự định nên tỉ lệ giữa vận tốc thực tế và vận tốc dự định là $\frac{4}{3}$.

Mà vận tốc và thời gian ô tô đi trên quãng đường AB là hai đại lượng tỉ lệ nghịch nên $\frac{6}{\mathrm{t}}=\frac{4}{3}$

Do đó $\mathrm{t}=\frac{6.3}{4}=\frac{9}{2}=4,5$ (h)

Vậy thời gian thực tế ô tô đã đi là 4,5 (h).

Bài 2. Biết 3 người làm cỏ trên một cánh đồng hết 6 giờ. Hỏi 12 người (với cùng năng suất như thế) làm cỏ trên cánh đồng đó hết bao nhiêu thời gian?

Hướng dẫn giải

Gọi x (người), y (giờ) lần lượt là số người và thời gian để số người đó hoàn thành việc làm cỏ trên cánh đồng. Khi đó ta có mỗi quan hệ giữa số người (x) và thời gian hoàn thành công việc (y) được cho bởi bảng sau:

Do thời gian hoàn thành công việc tỉ lệ nghịch với với số người làm việc theo hệ số tỉ lệ

a = x₁. y₁ = 3.6 = 18.

Suy ra 12 . y₂ = 18. Vì thế  y₂ = 18 : 12 = 1,5.

Vậy 12 người hoàn thành công việc làm cỏ trong 1,5 giờ.

B. Bài tập trắc nghiệm

Câu 1. Cho x và y là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a. Nếu x = −3 thì y = −12. Hệ số tỉ lệ a là:

A. 4;

B. −4;

C. 36;

D. −36.

Hướng dẫn giải

Đáp án đúng là: C.

Vì x và y là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a nên ta có xy = a.

Khi x = −3 thì y = −12 nên (−3).(−12) = a

Do đó a = 36.

Vậy hai đại lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ a = 36.

Câu 2. Một ô tô đi từ A đến B hết 4 giờ 30 phút. Hỏi ô tô đi từ A đến B hết mấy giờ nếu ô tô đi với vận tốc gấp đôi vận tốc cũ?

A. 2 giờ;

B. 2 giờ 15 phút;

C. 3 giờ;

D. 2 giờ 45 phút.

Hướng dẫn giải

Đáp án đúng là: B.

Đổi 4 giờ 30 phút = 4,5 giờ.

Gọi vận tốc cũ và vận tốc mới của ô tô lần lượt là v₁ (km/h) và v₂ (km/h).

Thời gian tương ứng của ô tô đi từ A đến B lần lượt là t₁ (giờ) và t₂ (giờ).

Mà vận tốc mới gấp đôi vận tốc cũ nên ta có v₂ = 2v₁.

Ta có vận tốc và thời gian của ô tô khi chuyển động trên cùng một quãng đường là hai đại lượng tỉ lệ nghịch.

Do đó ta có $\frac{{\mathrm{t}}_2}{{\mathrm{t}}_1}=\frac{{\mathrm{v}}_1}{{\mathrm{v}}_2}=\frac{{\mathrm{v}}_1}{2{\mathrm{v}}_1}=\frac{1}{2}$ hay $\frac{{\mathrm{t}}_2}{{\mathrm{t}}_1}=\frac{1}{2}$ 

Thay t₁ = 4,5 ta có $\frac{{\mathrm{t}}_2}{4,5}=\frac{1}{2}$ suy ra 2.t₂ = 4,5.1

Nên t₂ = 4,5 : 2 = 2,25 (giờ)

Đổi 2,25 giờ = 2 giờ 15 phút.

Vậy nếu đi với vận tốc gấp đôi vận tốc cũ thì ô tô đi hết 2 giờ 15 phút.

Câu 3. Chị Mai đi đổ xăng cho chiếc xe của mình thì đổ được 9 lít với số tiền định trước. Nhưng do giá xăng tăng nên chị chỉ đổ được 8 lít. Hỏi giá xăng đã tăng bao nhiêu phần trăm?

A. 112,5%;

B. 12,5%;

C. 25%;

D. 125%.

Hướng dẫn giải

Đáp án đúng là: B.

Gọi giá xăng trước khi tăng giá là x (nghìn đồng), giá xăng sau khi tăng giá là y (nghìn đồng).

Vì số tiền của chị Mai là không đổi nên giá xăng và số lít xăng mua được là hai đại lượng tỉ lệ nghịch.

Theo tính chất tỉ lệ nghịch ta có: 9x = 8y

Suy ra $\mathrm{y}=\frac{9}{8}\mathrm{x}$  

Đổi $\frac{9}{8}=1,125=\frac{112,5}{100}=112,5\%$

Do đó giá xăng tăng: 112,5% − 100% = 12,5%.

Vậy giá xăng tăng 12,5%.

2. Bài tập tự luyện có hướng dẫn

Xem thêm các dạng bài tập Toán khác :

70 Bài tập về đại lượng tỉ lệ nghịch (có đáp án năm 2023)

60 Bài tập về dãy tỉ số bằng nhau (có đáp án năm 2023)

60 Bài tập về tỉ lệ thức (có đáp án năm 2023)

60 Bài tập làm tròn số và ước lượng (có đáp án năm 2023)

60 Bài tập Tập hợp các số thực (có đáp án năm 2024)