60 Bài tập làm tròn số và ước lượng (có đáp án năm 2023) - Toán 7

Kiến thức cần nhớ

1. Làm tròn số

1.1 Số làm tròn

Ở nhiều tình huống thực tiễn ta cần tìm một số thực khác xấp xỉ với số thực đã cho để thuận tiện hơn trong ghi nhớ, đo đạc, hay tính toán. Số thực tìm được như thế được gọi là số làm tròn của số thực đã cho.

Ví dụ:

Hóa đơn tiền điện của gia đình bạn An tháng 9/2021 là 356 870 đồng. Trên thực tế mẹ của An đã trả tiền mặt cho người thu tiền điện 357 000 đồng.

Vậy số 357 000 là số làm tròn của số 356 870.

1.2 Làm tròn số với độ chính xác cho trước

Ta nói số a được làm tròn đến số b với độ chính xác d nếu khoảng cách giữa điểm a và điểm b trên trục số không vượt quá d.

Ví dụ: Làm tròn số 126 đến hàng chục ta được số 130. Khoảng cách giữa hai điểm 126 và 130 trên trục số là 130 – 126 = 4. Khoảng cách này không vượt quá 5. Khi đó ta nói số 126 được làm tròn đến số 130 với độ chính xác 5.

Nhận xét:

- Khi làm tròn số đến một hàng nào đó thì độ chính xác bằng nửa đơn vị của hàng làm tròn.

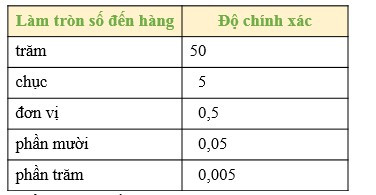
- Để làm tròn số với độ chính xác cho trước, ta có thể sử dụng cách ở bảng sau:

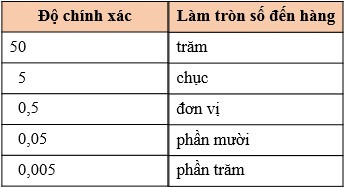
- Để làm tròn một số thập phân âm, ta chỉ cần làm tròn số đối của nó rồi đặt dấu “–” trước kết quả.

Ví dụ:

a) Làm tròn số 3,141592653… đến hàng phần trăm.

b) Làm tròn số 128,25 với độ chính xác 0,05.

c) Làm tròn số – 1,9254 với độ chính xác 0,005.

d) Làm tròn số $\sqrt{2}$ với độ chính xác 0,5.

Hướng dẫn giải

a) Ta áp dụng quy tắc làm tròn số thập phân hữu hạn. Do chữ số ở hàng phần nghìn là 1 < 5 nên 3,141592653… ≈ 3,14.

Người ta chứng minh được rằng số 3,141592653… làm tròn đến 3,14 cũng với độ chính xác 0,005.

b) Để làm tròn số 128,25 với độ chính xác 0,05 ta sẽ làm tròn đến hàng phần mười. Áp dụng quy tắc làm tròn số ta được 128,25 ≈ 128,3.

c) Để làm tròn số –1,9254 với độ chính xác 0,005 ta sẽ làm tròn đến hàng phần trăm. Áp dụng quy tắc làm tròn số ta được 1,9254 ≈ 1,93. Vì vậy, – 1,9254 ≈ –1,93.

d)

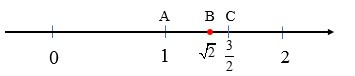
Ta biểu diễn số $\sqrt{2}$ trên trục số. Khi đó AC = 0,5, điểm B nằm giữa A và C nên AB < AC.

Mà AC = 0,5 nên AB < 0,5, tức là khoảng cách giữa điểm $\sqrt{2}$ và điểm 1 trên trục số nhỏ hơn 0,5. Vậy với độ chính xác 0,5 thì $\sqrt{2}$ ≈ 1.

Chú ý: Trong đo đạc và tính toán thực tiễn, ta thường có gắng làm tròn số thực với độ chính xác d nhỏ nhất càng tốt. Trong thực tế, làm tròn số thực là một công việc có nhiều khó khăn. Tuy nhiên, người ta cũng biết một số cách để làm tròn số thực.

2. Ước lượng

Trong thực tiễn, đôi lúc ta không quá quan tâm đến tính chính xác của kết quả tính toán mà chỉ cần ước lượng kết quả, tức là tìm một số gần sát với kết quả chính xác.

Ví dụ: Áp dụng quy tắc làm tròn để ước lượng kết quả của các phéo tính sau:

a) 5,14 + 4,93

b) 60,3 . 49,5

Hướng dẫn giải

a) Làm tròn đến hàng phần mười của mỗi số hạng: 5,14 ≈ 5,1;     4,93 ≈ 4,9

Khi đó 5,14 + 4, 93 ≈ 5,1 + 4,9 = 10.

b) Làm tròn đến hàng đơn vị mỗi thừa số ta có:  60,3 ≈ 60;  49,5 ≈ 50.

Khi đó 60,3 . 49,5 ≈ 60 . 50 = 3000.

Các dạng bài tập làm tròn số và ước lượng

Dạng 1: Làm tròn các số theo một yêu cầu cho trước.

1. Phương pháp giải:

- Áp dụng quy ước làm tròn số trong hai trường hợp.

- Chú ý hiểu đúng các cụm từ “làm tròn số đến chữ số thập phân thứ…”,

“làm tròn chữ số đến hàng…”.

2. Ví dụ minh họa:

Ví dụ 1:

a) Làm tròn số 23,1826 đến chữ số thập phân thứ ba;

b) Làm tròn số 23,1826 đến chữ số thập phân thứ hai;

c) Làm tròn số 23,1826 đến chữ số thập phân thứ nhất.

Giải:

a) 23,1826 $\approx$  23,183 (chữ số bỏ đi là 6 > 5).

b) 23,1826 $\approx$  23,18 (chữ số bỏ đi là 2 < 5).

c) 23,1826 $\approx$  23,2 (chữ số bỏ đi là 8 > 5).

Dạng 2: Giải bài toán rồi làm tròn kết quả.

1. Phương pháp giải:

Căn cứ vào đề bài, giải bài toán rồi làm tròn kết quả theo yêu cầu của đề bài. Chú ý đề bài yêu cầu “làm tròn đến chữ số thập phân thứ…” hoặc “làm tròn đến chữ số hang…”.

2. Ví dụ minh họa:

Ví dụ 2: Hết học kì I, điểm Toán của bạn An như sau:

Hệ số 1: 6 ; 8 ; 5 ; 9.

Hệ số 2: 7 ; 6 ; 8 ; 9.

Hệ số 3: 7.

Tìm điểm trung bình môn Toán học kì I của bạn An (làm tròn đến chữ số thập phân thứ nhất).

Giải:

Điểm trung bình môn Toán học kì I của bạn An là:

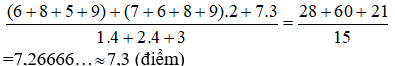
Vậy điểm trung bình môn Toán học kì I của bạn An là 7,3 điểm.

Dạng 3: Áp dụng quy ước làm tròn số để ước lượng kết quả các phép tính.

1. Phương pháp giải:

Để ước lượng kết quả các phép tính, ta thường áp dụng quy ước làm tròn số để làm tròn chữ số ở hàng cao nhất của mỗi số tham gia vào phép tính.

Ví dụ: Số 7329 được làm tròn số đến chữ số ở hàng cao nhất là $\approx$ 7000.

2. Ví dụ minh họa:

Ví dụ 3: Hãy ước lượng kết quả các phép tính sau:

a) 128.42                                                     b) 6921: 49

Giải:

a) 128.42 $\approx$  130.40 = 5200.

Tích phải tìm có 4 chữ số và xấp xỉ 5200.

b) 6921: 49 $\approx$  7000 : 50 = 140.

Thương phải tìm có 3 chữ số và xấp xỉ 140.

Bài tập tự luyện

1. Bài tập vận dụng

Bài 1: Làm tròn các số sau đây: 7842; 89367; 917527; 17493

a. Đến hàng trăm.

b. Đến hàng nghìn.

Bài 2: Tính trung bình cộng của các số 7; 5; 11 rồi làm tròn đến chữ số thập phân thứ ba.

Bài 3: Thực hiện phép tính rồi làm tròn kết quả đến chữ số thập phân thứ hai:

a) 4,5672 + 2,34 + 0,167

b) (2,364 + 8,2) – (7,002 + 0,17)

c) 78,2.4,006

Bài 4: Tổng kết năm học, bạn Ngân được điểm như sau: Toán: 7,8; Văn: 8,3; Lí: 7,0; Tiếng Anh: 7,5; Sử: 8,5; Địa: 9,0. Tính điểm trung bình các môn học của bạn Ngân (làm tròn kết quả đến chữ số thập phân thứ nhất).

Bài 5: Viết các phân số sau thành số thập phân, rồi làm tròn lần lượt các số đó đến chữ số thập phân thứ hai: $\frac{8}{33};\frac{26}{111};\frac{5}{24};\frac{15}{82}$

Bài 6: Một tam giác có cạnh đáy bằng $\frac{13}{2}cm$ . Cạnh đáy dài gấp rưỡi độ dài đường cao tương ứng và 1cm. Tính diện tích tam giác đó (làm tròn đến hàng đơn vị)

Bài 7: Làm tròn các số đến hàng đơn vị rồi tính kết quả của phép tính:

a) (0,93 + 1,72)(8,5 – 1,7)

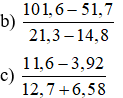
d) (4,62 + 21,7).4,21

Bài 8: Tính giá trị của biểu thức rồi làm tròn đến hàng đơn vị:

A = (9,126 : 0.65).718 + 1,45.28,20

$B=\frac{\left(11,81+8,19\right).2,25}{7,65}$

C = 50,93.49.49.15 – 59,83.29,21

Bài 9: Ba phân số tối giản có tổng bằng $3\frac{7}{60}$, các tử số của chúng tỉ lệ với 2 : 3 : 5, các mẫu của chúng tỉ lệ với 5 : 4 : 6. Đưa phân số này về dạng số thập phân và làm tròn đến chữ số thập phân thứ ba.

Bài 10: Tìm x, làm tròn x đến số thập phân thứ ba:

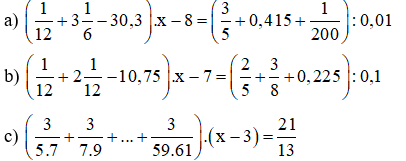
Hướng dẫn giải:

Bài 1:

a) Làm tròn đến chữ số hàng trăm: 7800; 89400; 917500; 17500.

b) Làm tròn đến chữ số hàng nghìn: 8000; 89000; 918000; 17000.

Bài 2:

Trung bình cộng của ba số 7; 5; 11 là: $\frac{7+5+11}{3}=7,66666...\approx 7,667$

Bài 3:

a) 11,3392 $\approx$ 11,34

b) 3,392 $\approx$ 3,39

c) 313,2692 $\approx$ 313,27

Bài 4:

Bài 5:

Bài 6:

Độ dài đường cao của tam giác là:$\frac{13}{2}:\frac{3}{2}-1=\frac{10}{3}\left(cm\right)$ .

Diện tích tam giác là: $\frac{1}{2}.\frac{13}{2}.\frac{10}{3}=\frac{130}{12}=10,8333...\approx 11\left(c{m}^2\right)$

Bài 7:

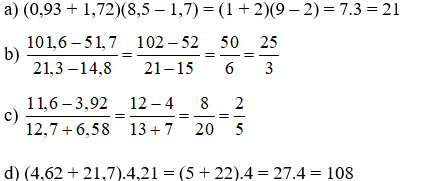
Bài 8: Đáp án:

A = 142

B = 6

C = 2

Bài 9: 

Bài 10: Tìm x, làm tròn x đến số thập phân thứ ba:

a) x $\approx$ – 4,067

b) x $\approx$ – 1,981

c) x $\approx$ – 8,865

2. Bài tập tự luyện có hướng dẫn