50 bài tập về hình vuông (có đáp án 2024) – Toán 8

Các dạng toán về Hình vuông và cách giải - Toán lớp 8

I. Kiến thức cần nhớ

1. Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

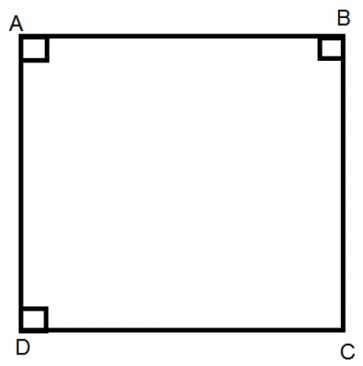
Tứ giác ABCD là hình vuông

$\iff \left\{\begin{array}{l}\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}={90}^o\\ AB=BC=CD=DA\end{array}\right.$

Nhận xét:

a) Hình vuông là một hình chữ nhật có 4 cạnh bằng nhau.

b) Hình vuông là hình thoi có 4 góc bằng nhau.

Như vậy hình vuông vừa là hình chữ nhật, vừa là hình thoi.

2. Tính chất

Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

3. Dấu hiệu nhận biết

a) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

b) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

c) Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

d) Hình thoi có một góc vuông là hình vuông.

e) Hình thoi có hai đường chéo bằng nhau là hình vuông.

II. Các dạng toán và phương pháp giải

Dạng 1: Chứng minh tứ giác là hình vuông

Phương pháp giải: Vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình vuông.

Ví dụ: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Chứng minh tứ giác EFGH là hình vuông.

Lời giải:

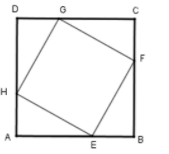
Vì ABCD là hình vuông nên AB = BC = CD = DA và $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90°$

Ta có: 

$\left\{\begin{array}{l}AB=AE+EB\\ BC=BF+CF\\ CD=CG+DG\\ AD=DH+AH\end{array}\right.$mà AB = BC = CD = DA và AE = BF = CG = DH

Nên EB = CF = DG = AH

Xét tam giác AHE và tam giác BEF có

$\widehat{A}=\widehat{B}=90°$

AH = BE (chứng minh trên)

AE = BF (giả thuyết)

Do đó: $\Delta AHE=\Delta BE\text{}F$ (c – g – c)

$\Rightarrow$HE = EF (hai cạnh tương ứng) (1); $\widehat{AEH}=\widehat{E\text{}FB}$ (hai góc tương ứng)

Xét tam giác CFG và tam giác DGH có

$\widehat{C}=\widehat{D}=90°$

CF = DG (chứng minh trên)

CG = DH (giả thiết)

Do đó: $\Delta CFG=\Delta DGH$ (c – g – c)

$\Rightarrow$FG = GH (hai cạnh tương ứng) (2)

Xét tam giác CFG và tam giác AHE có

$\widehat{C}=\widehat{A}=90°$

CF = AH(chứng minh trên)

CG = AE (giả thiết)

Do đó: $\Delta CFG=\Delta AHE$ (c – g – c)

$\Rightarrow$FG = HE (hai cạnh tương ứng) (3)

Xét tứ giác EFGH ta có:

FG = HE = GH = EF (theo (1), (2), (3))

Nên tứ giác EFGH là hình thoi

Lại có:

$\widehat{FEB}+\widehat{E\text{}FB}=90°$ (do tam giác vuông)

Mà $\widehat{AEH}=\widehat{E\text{}FB}$ (chứng minh trên)

Nên $\widehat{AEH}+\widehat{FEB}=90°$

Mặt khác:

$\widehat{AEH}+\widehat{HE\text{}F}+\widehat{FEB}=180°$

$\Rightarrow \widehat{HE\text{}F}=90°$

Mà hình thoi EFGH có một góc vuông nên hình thoi EFGH là hình vuông.

Dạng 2: Vận dụng tính chất của hình vuông để chứng minh các tính chất hình học

Phương pháp giải: Vận dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình vuông.

Ví dụ: Cho hình vuông ABCD. Trên cạnh AD, DC lần lượt lấy các điểm E, F sao cho AE = DF. Chứng minh:

a) Hai tam giác ADF và BAE bằng nhau;

b) BE vuông góc với AF.

Lời giải:

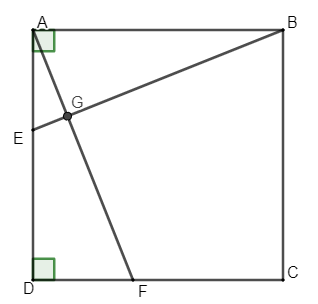
a) Vì ABCD là hình vuông nên AB = AD và $\widehat{D}=\widehat{EAB}=90°$

Xét hai tam giác ADF và BAE ta có: 

AD = AB

$\widehat{D}=\widehat{EAB}=90°$

AE = DF ( giả thiết)

Do đó: $\Delta ADF=\Delta BAE$ (c – g – c)

b) Gọi giao điểm của BE và AF là G.

Ta có:

$\widehat{DFA}+\widehat{DA\text{}F}=90°$

Mà $\widehat{DFA}=\widehat{AEB}$ (hai góc tương ứng của hai tam giác bằng nhau $\Delta ADF=\Delta BAE$)

Nên $\widehat{AEB}+\widehat{DA\text{}F}=90°$ hay $\widehat{AEG}+\widehat{EAG}=90°$

Mà theo định lý tổng ba góc trong tam giác AEG ta có:

$\begin{array}{l}\widehat{AGE}+\widehat{AEG}+\widehat{EAG}=180°\\ \Rightarrow \widehat{AGE}+90°=180°\\ \Rightarrow \widehat{AGE}=90°\end{array}$

$\Rightarrow BE\perp AF$ tại G.

Dạng 3: Tìm điều kiện để tứ giác là hình vuông

Phương pháp giải: Vận dụng định nghĩa và các tính chất và dấu hiệu nhận biết của hình vuông.

Ví dụ: Cho tam giác ABC vuông cân tại A, M là một điểm thuộc cạnh BC. Qua M vẽ các đường thẳng song song với AC, AB chúng cắt các cạnh AB, AC theo thứ tự tại E và F.

a) Tứ giác AFME là hình gì?

b) Xác định vị trí điểm M trên cạnh BC để tứ giác AFME là hình vuông.

Lời giải

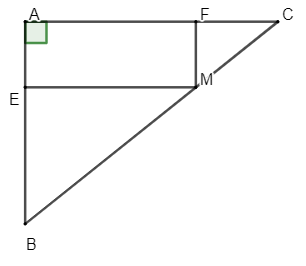
a) Ta có tam giác ABC vuông tại A nên

Vì MF // AB nên $MF\perp AC$$\Rightarrow \widehat{A\text{}FM}=90°$

Vì ME // AC nên $ME\perp AB$$\Rightarrow \widehat{AEM}=90°$

Xét tứ giác AFME có:

$\begin{array}{l}\widehat{A\text{}FM}=90°\\ \widehat{AEM}=90°\\ \widehat{A}=90°\end{array}$

Do đó tứ giác AFME là hình chữ nhật.

b) Để tứ giác AFME là hình vuông thì MF = ME (hình chữ nhật có hai cạnh kề bằng nhau).

Ta có: $\widehat{B}=\widehat{C}$ (do tam giác ABC cân tại A)

Mà $\widehat{B}+\widehat{EMB}=90°$ (tam giác MEB vuông tại E); $\widehat{C}+\widehat{FMC}=90°$ (tam giác FMC vuông tại F)

Suy ra $\widehat{EMB}=\widehat{FMC}$

Xét tam giác MFC và tam giác MEB có

$\widehat{MFC}=\widehat{MEB}=90°$

MF = ME (giả thuyết hình vuông)

$\widehat{EMB}=\widehat{FMC}$ (cmt)

Do đó: $\Delta MFC=\Delta MEB$ (cạnh góc vuông và góc nhọn kề nó)

$\Rightarrow$ MB = MC (hai cạnh tương ứng) hay M là trung điểm của BC.

Vậy để AFME là hình vuông khi M là trung điểm của BC.

III. Bài tập tự luyện

Bài 1: Cho hình vuông ABCD. Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE = CF.

a) Chứng minh tam giác EDF vuông cân.

b) Gọi I là trung điểm của EF. Chứng minh BI = DI.

c) Chứng minh A, C, I thẳng hàng.

Bài 2: Cho tứ giác ABCD. Gọi E, F, G, H theo thứu tự là trung điểm của AB, BC, CD, AD. Tìm điều kiện của tứ giác ABCD để tứ giác EFGH là

a) Hình chữ nhật;

b) Hình thoi;

c) Hình vuông.

Bài 3: Cho hình vuông ABCD, lấy M bất kỳ trên cạnh DC. Tia phân giác $\widehat{MAD}$ cắt CD tại I. Kẻ IH vuông góc với AM tại H, tia IH cắt BC tại K. Chứng minh:

a) $\Delta ABK=\Delta AHK$

b) $\widehat{IAK}=45°$

Bài 4: Cho đoạn thẳng AB và điểm M thuộc đoạn thẳng đó. Vẽ về một phía của AB, các hình vuông AMCD, BMEF.

a) Chứng minh AE vuông góc với BC.

b) Gọi H là giao điểm của AE và BC. Chứng minh ba điểm D, H, F thẳng hàng.

c) Chứng minh đường thẳng DF luôn đi qua một điểm cố định khi M di chuyển trên đoạn thẳng cố định AB.

Bài 5: Cho tam giác ABC, vẽ ra phía ngoài tam giác các hình vuông ABDE và  BCKH. BM là đường trung tuyến của tam giác ABC.

a) Chứng minh: $\widehat{DBH}+\widehat{ABC}=180°$;

b) Vẽ hình bình hành DBHN. Chứng minh $\Delta ABC=\Delta NHB$;

c) Chứng minh: DH = 2BM;

d) Chứng minh BM vuông góc với DH.

Bài 6: Cho hình vuông ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Kẻ OF vuông góc với AD, OG vuông góc với CD. Chứng minh:

a) OB = FG và OB vuông góc với FG;

b) Các đường thẳng BO, AG, CF đồng quy.

Bài 7: Cho hình vuông ABCD. Gọi I, K lần lượt là trung điểm của AD và DC

a) Chứng minh rằng BI vuông góc với AK;

b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.

Bài 8: Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC và CD lần lượt lấy hai điểm M và N sao cho $\widehat{MAN}=45°$. Trên tia đối của tia DC lấy điểm K sao cho DK = BM. Hãy tính:

a) Số đo $\widehat{KAN}$;

b) Chu vi tam giác MCN theo a.

Bài 9: Trên các cạnh BC, CD của hình vuông ABCD với AB = 1, ta lấy được các điểm M, N tương ứng sao cho chu vi tam giác MCN bằng 2.

a) Chứng minh: $\widehat{MAN}=45°$

b) Gọi P và Q là giao điểm của BD với các đoạn thẳng AM, AN. Chứng minh các đoạn thẳng BP, PQ, QD lập thành ba cạnh của một tam giác vuông.

Bài 10: Cho tứ giác ABCD có $\widehat{ADC}+\widehat{BCD}=90°$. Gọi I, N, J, M lần lượt là trung điểm của AB, AC, CD, BD. Chứng minhtức giác INJM là hình vuông.

Xem thêm các dạng bài tập hay, có đáp án:

60 Bài tập về hình tam giác, hình tứ giác. Hình chữ nhật, hình vuông (có đáp án năm 2024) - Toán lớp 3

60 Bài tập về chu vi hình tam giác, hình tứ giác, hình chữ nhật, hình vuông (có đáp án năm 2024) - Toán lớp 3

50 Bài tập về hình vuông - hình tròn - hình tam giác - hình chữ nhật (có đáp án năm 2024) - Toán lớp 1

50 Bài tập về hình tam giác đều. hình vuông. hình lục giác đều (có đáp án năm 2024) - Toán 6

50 bài tập về hình thang, hình thang vuông, hình thang cân (có đáp án 2024) – Toán 8