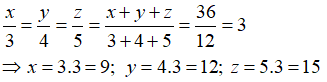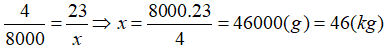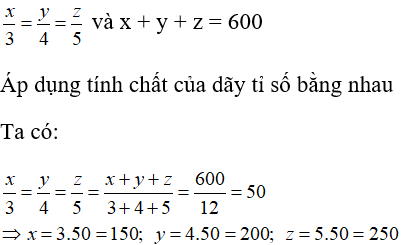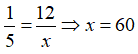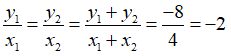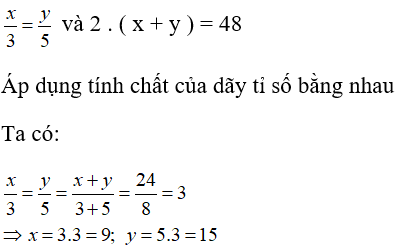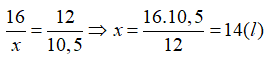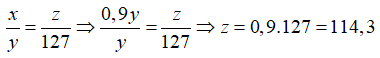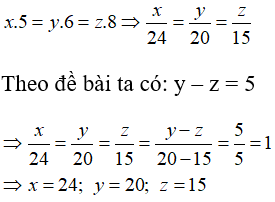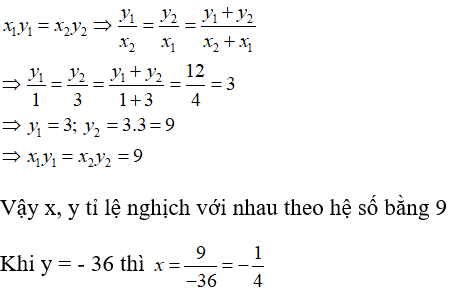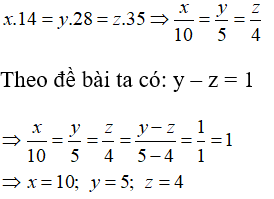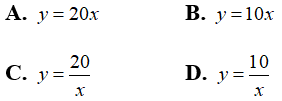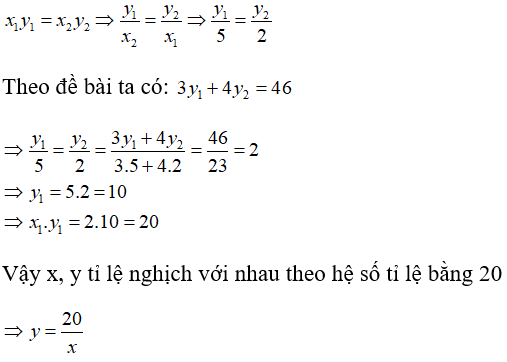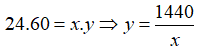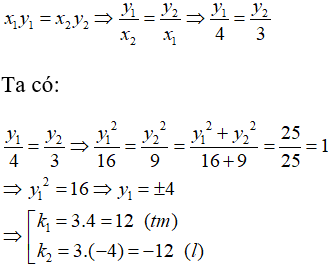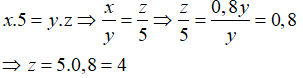Cách giải bài toán tỉ lệ thuận, tỉ lệ nghịch
CÁC DẠNG TOÁN
Dạng 1. Bài toán về đại lượng tỉ lệ thuận
1. Phương pháp
Cách 1. Rút về đơn vị
Cách 2. Dùng tỉ số
2. Ví dụ
Ví dụ 1. May ba bộ quần áo như nhau hết 15 mét vải. Hỏi may 9 bộ quần áo như thế hết mấy mét vải?
Tóm tắt:
3 bộ quần áo hết 15m vải
9 bộ quần áo hết ?m vải
Bài giải
Cách 1. Rút về đơn vị
May một bộ quần áo hết:
15 : 3 = 5 (m)
May 9 bộ quần áo như thế hết số mét vải là:
5 × 9 = 45 (m)
Cách 2. Dùng tỉ số
9 bộ quần áo gấp 3 bộ quần áo số lần là:
9 : 3 = 3 (lần)
May 9 bộ quần áo hết số mét vải là:
5 × 9 = 45 (m)
Đáp số: 45m
Ví dụ 2. Nếu 5 người, mỗi người làm việc trong 6 giờ thì được nhận 150000 đồng. Hỏi nếu 15 người, mỗi người làm việc trong 6 giờ thì được nhận bao nhiêu tiền? (Giá trị giờ công của mỗi người là như nhau).
Lời giải:
15 người so với 5 người thì gấp:
15 : 5 = 3 (lần)
15 người, mỗi người làm việc 6 giờ thì được nhận số tiền là:
150000 × 3 = 450000 (đồng)
Đáp số: 450000 đồng
Dạng 2. Bài toán về đại lượng tỉ lệ nghịch
1. Phương pháp
Cách 1. Rút về đơn vị
Cách 2. Dùng tỉ số
2. Ví dụ
Ví dụ 1. 14 người đắp xong một đoạn đường trong 6 ngày. Hỏi 28 người đắp xong đoạn đường đó trong bao nhiêu ngày? (Năng suất lao động của mỗi người như nhau)
Bài giải
Cách 1. Rút về đơn vị
Một người đắp xong đoạn đường đó trong số ngày là:
6 × 14 = 84 (ngày)
28 người đắp xong đoạn đường đó trong số ngày là:
84 : 28 = 3 (ngày)
Cách 2. Dùng tỉ số
28 người gấp 14 người số lần là:
28 : 14 = 2 (lần)
28 người đắp xong đoạn đường đó trong số ngày là:
6 : 2 = 3 (ngày)
Đáp số: 3 ngày
Ví dụ 2 : Nếu có 4 người mỗi ngày làm việc 5 giờ thì đắp xong đoạn đường trong 12 ngày. Hỏi nếu có 6 người mỗi ngày làm việc 10 giờ thì đắp xong đoạn đường ấy trong bao nhiêu ngày (năng suất lao động của mỗi người như nhau).
Tóm tắt:
4 người mỗi ngày làm 5 giờ: 12 ngày
6 người mỗi ngày làm 10 giờ: ? ngày
Bài giải
Một người mỗi ngày làm việc 5 giờ thì đắp xong đoạn đường trong số ngày là:
4 × 12 = 48 (ngày)
Một người mỗi ngày làm việc 10 giờ thì đắp xong đoạn đường trong số ngày là:
48 : 2 = 24 (ngày)
6 người mỗi ngày làm việc 10 giờ thì đắp xong đoạn đường trong số ngày là
24 : 6 = 4 (ngày)
Đáp số: 4 ngày
Dạng 3. Bài toán về mối quan hệ giữa đại lượng tỉ lệ thuận và đại lượng tỉ lệ nghịch
1. Phương pháp
Bước 1. Phân tích bài toán, nhận dạng toán tỉ lệ thuận hay tỉ lệ nghịch
Bước 2. Áp dụng 1 trong các cách (Rút về đơn vị, Rút về tỉ số, có thể áp dụng công thức tam suất) để giải bài toán.
Bước 3. Kết luận, đáp số
2. Ví dụ
Ví dụ 1. Một tốp thợ có 120 người dự định làm trong 50 ngày. Khi bắt đầu làm có thêm một số người đến thêm nên làm xong công việc đó trong 30 ngày. Hỏi có bao nhiêu người đến thêm?
Bài giải
Số ngày công hoàn thành công việc:
50 × 120 = 6000 (ngày)
Số người thợ để hoàn thành công việc trong 30 ngày:
6000 : 30 = 200 (người)
Số người đến thêm:
200 – 120 = 80 (người)
Đáp số: 80 người
Ví dụ 2. Một bếp ăn chuẩn bị một số gạo đủ cho 120 người ăn trong 40 ngày. Sau khi ăn hết một nửa số gạo đó bếp ăn nhận thêm một số người nên số gạo còn lại chỉ đủ cho bếp ăn trong 12 ngày nữa (mức ăn của mỗi người không thay đổi). Hỏi bếp ăn đã nhận thêm bao nhiêu người nữa?
Bài giải
Sau khi hết nửa số gạo thì 120 người sẽ ăn trong thời gian còn lại:
40 : 2 = 20 (ngày)
Nếu 1 người ăn nửa số gạo phải mất thời gian:
20 × 120 = 2400 (ngày)
Số người ăn nửa số gạo trong 12 ngày:
2400 : 12 = 200 (người)
Số người mà bếp ăn đã nhận thêm:
200 – 120 = 80 (người)
Đáp số: 80 người
Ví dụ 3. 12 công nhân trong một ngày dệt được 120 tá áo. Hỏi với mức làm như vậy, muốn dệt 180 tá áo như thế trong một ngày cần bao nhiêu công nhân?
Bài giải
Một công nhân một ngày dệt được số tá áo là:
120 : 12 = 10 (tá áo)
Muốn dệt 180 tá áo như thế trong một ngày cần số công nhân là:
180 : 10 = 18 (công nhân)
Đáp số: 18 công nhân
BÀI TẬP (có đáp án)
Bài tập vận dụng
Bài 1: Biết các cạnh của một tam giác tỉ lệ với 3; 4; 5 và chu vi của nó là 36cm. Tính các cạnh của tam giác đó
A. 9cm; 12cm; 15cm
B. 10cm; 12cm; 14cm
C. 8cm; 12cm; 16cm
D. 8cm; 10cm; 18cm
Lời giải:
Gọi độ dài các cạnh của tam giác lần lượt là x, y, z
Theo đề bài ta có: 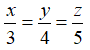
Theo tính chất của dãy tỉ số bằng nhau ta có:
Chọn đáp án A
Bài 2: Học sinh của ba lớp 6 cần phải trồng và chăm sóc 48 cây xanh. Lớp 6A có 28 học sinh, lớp 6B có 32 học sinh, lớp 6C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh biết số học sinh tỉ lệ với số cây xanh?
A. 14; 15 và 19
B. 15; 16 và 17
C. 14; 16 và 18
D. 13; 16 và 19
Lời giải:
Gọi số cây xanh mà ba lớp 6A, 6B, 6C phải trồng lần lượt là x, y, z cây
Vì số cây xanh tỉ lệ với số học sinh nên :
Chọn đáp án C
Bài 3: 4m dây đồng nặng 23g. Hỏi 8km dây đồng như thế nặng bao nhiêu kg?
A. 11,5 kg
B. 34,5 kg
C. 46kg
D. 69kg
Lời giải:
8km = 8 000 m
Gọi khối lượng của 8km dây đồng là x (g)
Vì chiều dài và khối lượng của dây đồng là hai đại lượng tỉ lệ nên ta có:
Chọn đáp án C
Bài 4: Ba đơn vị kinh doanh góp vốn theo tỉ lệ 3: 4: 5. Hỏi mỗi đơn vị được chia bao nhiêu tiền lãi nếu tổng số tiền lãi là 600 triệu đồng và tiền lãi được chia tỉ lệ thuận với số vốn đã đóng?
A. 120; 200 và 280
B. 130; 200 và 270
C. 140; 200 và 260
D. 150; 200 và 250
Lời giải:
Gọi số tiền lãi mà ba đơn vị được chia là x, y, z
Theo đề bài ta có:
Chọn đáp án D
Bài 5: Biết độ dài các cạnh của một tam giác tỉ lệ với 4: 5: 6 . Tính độ dài mỗi cạnh của tam giác đó, biết rằng cạnh lớn nhất dài hơn cạnh nhỏ nhất là 8cm.
A. 16; 20 và 24
B. 18; 20 và 26
C. 20; 24 và 28
D. 20; 22 và 28
Lời giải:
Gọi độ dài các cạnh của tam giác lần lượt là x, y, z (cm)
Theo đề bài ta có:
Chọn đáp án A
Bài 6: Trên một chiếc đồng hồ, khi kim giờ quay đúng năm vòng thì số vòng kim phút quay được là:
A. 15
B. 36
C. 60
D. 300
Lời giải:
Ta có: khi kim giờ quay được một vòng thì kim phút quay được 12 vòng
Gọi số vòng kim phút quay được khi kim giờ quay được năm vòng là x ( vòng)
Vì số vòng kim giờ và kim phút quay được là tỉ lệ nên ta có:
Chọn đáp án C
Bài 7: Cho x và y là hai đại lượng tỉ lệ thuận. Khi các giá trị x1, x2 của x có tổng bằng 4 thì giá trị tương ứng y1, y2 có tổng bằng – 8 . Tính giá trị của y khi x = - 2
A. – 1
B. 1
C. – 4
D. 4
Lời giải:
Vì x và y là hai đại lượng tỉ lệ thuận nên ta có:
Vậy y tỉ lệ với x theo hệ số tỉ lệ là – 2 : y = -2x
Với x = -2 thì y = (-2). (-2) = 4
Chọn đáp án D
Bài 8: Chu vi của một hình chữ nhật là 48cm. Tính độ dài mỗi cạnh biết chúng tỉ lệ với 3 và 5
A. 9cm và 15cm
B. 8cm và 16cm
C. 10cm và 14cm
D. 11cm và 13cm
Lời giải:
Gọi độ dài chiều rộng và chiều dài của hình chữ nhật là x, y (cm)
Theo đầu bài ta có:
Chọn đáp án A
Bài 9: Gọi x, y, z theo thứ tự là số vòng quay của kim giờ, kim phút và kim giây trong cùng một thời gian. Tìm hệ số tỉ lệ của z đối với x
A. 60
B. 120
C. 360
D. 720
Lời giải:
Trên đồng hồ có 12 số chia mặt đồng hồ thành 12 khoảng bằng nhau
Khi kim phút quay được một vòng thì kim giờ quay được một khoảng. Do đó, khi kim phút quay được 12 vòng thì kim giờ quay được một vòng
Vậy y tỉ lệ với x theo hệ số tỉ lệ là 12: y = 12x
Khi kim giây quay được 60 vòng thì kim phút quay được một vòng. Do đó, z tỉ lệ với y theo hệ số tỉ lệ là 60: z = 60y
Suy ra, z = 60y = 60. 12x = 720 x
Vậy z tỉ lệ với x theo hệ số tỉ lệ là 720
Chọn đáp án D
Bài 10: Biết rằng 16l xăng nặng 12kg. Hỏi 10,5kg xăng có chứa được hết vào chiếc can bao nhiêu lít?
A. 11(l)
B. 12 (l)
C. 13 (l)
D. 14(l)
Lời giải:
Gọi thể tích của 10,5kg xăng là x (l)
Vì khối lượng và thể tích của xăng là hai đại lượng tỉ lệ thuận nên ta có:
Chọn đáp án D
Bài 1: Với số tiền để mua 127 mét vải loại I có thể mua được bao nhiêu mét vải loại II, biết rằng giá tiền vải loại I bằng 90% giá tiền vải loại II
A. 111,3
B. 112,3
C. 113,4
D. 114,3
Lời giải:
Gọi giá tiền vải loại I, II lần lượt là x, y
Theo đầu bài ta có: x = 0,9y
Gọi z là số mét vải loại II mua được
Với cùng số tiền, giá tiền và số mét vải mua được là hai đại lượng tỉ lệ nghịch:
Chọn đáp án D
Bài 2: Ba đội máy cày, cày ba cánh đồng cùng diện tích. Đội thứ nhất cày xong trong 5 ngày, đội thứ hai cày xong trong 6 ngày và đội thứ ba trong 8 ngày. Hỏi mỗi đội có bao nhiêu máy, biết rằng đội thứ hai có nhiều hơn đội thứ ba 5 máy? (Năng suất các máy như nhau)
A. 24; 20 và 15
B. 26; 18 và 15
C. 24; 18 và 13
D. 26; 16 và 11
Lời giải:
Gọi số máy cày của ba đội lần lượt là x, y, z (máy)
Vì diện tích cày là như nhau nên số máy cày và thời gian là hai đại lượng tỉ lệ nghịch
Chọn đáp án A
Bài 3: Cho x, y là hai đại lượng tỉ lệ nghịch với nhau. Khi x nhận các giá trị x1 = 3; x2 = 1 thì các giá trị tương ứng có tổng bằng 12. Khi y = -36 thì x bằng:
Lời giải:
Vì x, y là hai đại lượng tỉ lệ nghịch với nhau nên ta có:
Chọn đáp án C
Bài 4: Ba hộ gia đình cùng được phân phát một lượng gạo hỗ trợ dịch. Gia đình thứ nhất ăn hết số gạo trong 14 ngày, gia đình thứ hai ăn hết trong 28 ngày và gia đình thứ ba ăn hết trong 35 ngày. Hỏi mỗi gia đình có bao nhiêu thành viên biết gia đình thứ hai nhiều hơn gia đình thứ ba 1 người và coi lượng tiêu thụ thực phẩm của mỗi người là như nhau?
A. 12; 6 và 5
B. 11; 5 và 4
C. 10; 5 và 4
D. 10; 6 và 5
Lời giải:
Gọi số thành viên của mỗi gia đình lần lượt là x, y, z ( người)
Vì số thành viên và thời gian tiêu thụ hết thực phẩm là hai đại lượng tỉ lệ nghịch nên:
Chọn đáp án C
Bài 5: Cho x và y là hai đại lượng tỉ lệ nghịch với nhau. Khi x nhận các giá trị x1 = 2; x2 = 5 thì các giá trị tương ứng y1, y2 thỏa mãn: 3y1 + 4y2 = 46 . Hãy biểu diễn y qua x
Lời giải:
Do x, y là hai đại lượng tỉ lệ nghịch nên ta có:
Chọn đáp án C
Bài 6: Một bánh xe răng cưa có 24 răng ( quay được 60 vòng trong 1 phút). Nó khớp với một bánh xe răng cưa khác có x răng. Giả sử bánh xe răng cưa thứ hai quay được y vòng trong 1 phút. Hãy biểu diễn y theo x
Lời giải:
Ta có số răng cưa và số vòng quay là hai đại lượng tỉ lệ nghịch nên:
Chọn đáp án B
Bài 7: Cho x và y là hai đại lượng tỉ lệ nghịch với nhau. Khi x nhận các giá trị x1 = 3, x2 = 4 thì các giá trị y1, y2 thỏa mãn y12 + y22 = 25 . Hệ số tỉ lệ k (k > 0) giữa hai đại lượng là?
A. k = 3
B. k = 6
C. k = 9
D. k = 12
Lời giải:
Vì x, y là hai đại lượng tỉ lệ nghịch nên
Chọn đáp án D
Bài 8: Cho biết 3 người làm cỏ một cánh đồng hết 8 giờ. Hỏi 8 người ( với cùng năng suất như thế ) làm cỏ cánh đồng đó hết bao nhiêu giờ?
A. 2
B. 3
C. 4
D. 5
Lời giải:
Gọi thời gian 8 người làm cỏ cánh đồng hết x ( giờ)
Vì số người và thời gian là hai đại lượng tỉ lệ nghịch nên:
3.8 = 8.x ⇒ x = 3
Chọn đáp án B
Bài 9: Hai phân xưởng được giao may một số lượng áo len nhất định. Phân xưởng thứ nhất hoàn thành trong 5 ngày. Hỏi phân xưởng thứ hai hoàn thành trong bao nhiêu ngày biết số người của phân xưởng thứ nhất bằng 80% số người của phân xưởng thứ hai ( coi năng suất làm việc của mỗi người là như nhau)?
A. 2
B. 3
C. 4
D. 5
Lời giải:
Gọi số người của mỗi phân xưởng lần lượt là x, y ( người)
Số ngày phân xưởng thứ hai hoàn thành công việc là z ( ngày)
Theo đề bài ta có: x = 0,8y
Vì số người và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên:
Chọn đáp án C
Bài 10: Hai đại lượng x và y tỉ lệ nghịch với nhau. Khi x nhận các giá trị x1 = 2, x2 = 3 thì các giá trị tương ứng y1 = 36, y2 = 24. Hãy biểu diễn x theo y?
A. x = 72y
B. y = 72x
C. x = 72/y
D. y = 72/x
Lời giải:
Hai đại lượng x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ
Chọn đáp án C
Bài tập tự luyện
Bài 1: Tổ 1 lớp 5A có 11 em trồng được 44 cây, hỏi cả lớp nếu 48 em trồng được bao nhiêu cây, biết số cây mỗi em trồng được là như nhau.
Bài 2: Một tổ thợ mộc có 3 người trong 5 ngày đóng được 75 cái ghế. Hỏi nếu tổ đó có 5 người làm trong 7 ngày thì sẽ đóng được bao nhiêu cái ghế ? (biết năng suất mỗi người đều như nhau).
Bài 3: Một trường học huy động học sinh đi cuốc đất tăng gia, hôm đầu 30 em cuốc đất trong 2 giờ được . Hỏi hôm sau 50 em cuốc đất trong 3 giờ được bao nhiêu mét vuông ? (biết năng suất mỗi em đều như nhau)
Bài 4: 5 học sinh may 15 cái áo trong 3 giờ. Hỏi 8 học sinh may 32 cái áo mất bao lâu ? (biết năng suất mỗi người như nhau)
Bài 5: 8 người đóng xong 500 viên gạch trong 4 giờ. Hỏi 16 người đóng xong 1000 viên gạch mất bao lâu ? Biết năng suất mỗi người đều như nhau.
Bài 6: 9 người cuốc đất xong trong 5 giờ. Hỏi 18 người cốc đất xong trong bao lâu? (Biết năng suất mỗi người đều như nhau)
Bài 7: Một đơn vị bộ đội chuẩn bị đủ gạo cho 50 người ăn trong 10 ngày. 3 ngày sau được tăng thêm 20 người. Hỏi đơn vị cần chuẩn bị thêm bao nhiêu suất gạo nữa để đủ ăn trong những ngày sau đó (số gạo mỗi người ăn trong 1 ngày là một suất gạo)
Bài 8: Một đơn vị thanh niên xung phong chuẩn bị gạo đủ cho đơn vị ăn trong 30 ngày. Sau 10 ngày đơn vị nhận thêm 10 người nữa. Hỏi số gạo còn lại đó đơn vị sẽ đủ ăn trong bao nhiêu ngày? Biết lúc đầu đơn vị có 90 người.
Bài 9: 12 chị công nhân dệt trong 3 ngày được 120 tá áo. Hỏi nếu muốn dệt 180 tá áo trong 2 ngày cần bao nhiêu công nhân. Biết năng suất mỗi người như nhau.
Bài 10: Một cửa hàng có một số lít nước mắm đựng đầy trong các thùng, mỗi thùng chứa được 20 lít. Nếu đổ đủ số nước mắm đó vào các can, mỗi can chứa 5 lít, thì số can 5 lít phải nhiều hơn số thùng 20 lít là 30 cái. Hỏi cửa hàng có tất cả bao nhiêu lít nước mắm?
Bài 11: An và Bình cùng đọc một quyển truyện giống nhau. Trung bình mỗi ngày An đọc được 10 trang, Bình đọc được 15 trang. Hỏi quyển truyện dày bao nhiêu trang, biết An bắt đầu đọc sau Bình 2 ngày và Bình đọc xong trước An 7 ngày
Bài 12: Hai vòi nước cùng chảy vào một bể (không có nước) sau 6 giờ sẽ đầy bể. Hỏi nếu vòi một chảy một mình thì sau 10 giờ mới đầy bể. Hỏi nếu vòi hai chảy riêng một mình thì sau bao lâu sẽ đầy bể?
Bài 13: Một người đi từ tỉnh A đến tỉnh B bằng xe đạp, mỗi giờ đi được 12km. Từ B về A người đó đi bằng ô tô, mỗi giờ đi được 48km. Cả đi lẫn về mất 10 giờ. Hỏi quãng đường từ tỉnh A đến tỉnh B dài bao nhiêu ki – lô – mét?
Bài 14: Một cửa hàng có 28 thùng đựng đầy dầu gồm hai loại, loại thùng 60 lít và loại thùng 20 lít. Hỏi có bao nhiêu thùng mỗi loại, biết số dầu ở mỗi loại thùng đều bằng nhau.
Bài 2. Một tổ lao động tham gia trồng cây gây rừng, người ta dự định chia mỗi nhóm 12 người thì phải trồng 180 cây nhưng thực tế tổ làm tích cực hơn nên mỗi người trồng hơn dự định 2 cây và cả tổ trồng được 765 cây. Hỏi lúc đầu tổ lao động đó dự định trồng bao nhiêu cây?
Bài 3:
Một bếp ăn chuẩn bị một số gạo đủ cho 120 người ăn trong 40 ngày. Sau khi ăn hết một nửa số gạo đó bếp ăn nhận thêm một số người nên số gạo còn lại chỉ đủ cho bếp ăn trong 12 ngày nữa ( mức ăn của mỗi người không thay đổi). Hỏi bếp ăn đã nhận thêm bao nhiêu người nữa?
Bài 4:
Hai tổ công nhân tham gia làm một công việc. Nếu riêng tổ một làm thì 15 ngày sẽ hoàn thành công việc. Nếu riêng tổ hai làm thì 12 ngày sẽ hoàn thành công việc. Hỏi nếu 1/2 số công nhân tổ một và 1/5 số công nhân tổ hai cùng làm thì sẽ hoàn thành công việc sao bao nhiêu ngày?
Bai 5:
Một đội công nhân có 300 người dự định làm xong quảng đường trong 20 ngày. Sau khi làm được 10 ngày thì nhờ máy móc nên năng suất tăng gấp đôi. Hỏi đội công nhân đó hoàn thành sớm hơn dự định bao nhiêu ngày?
Bai 8. Một bếp ăn dự trữ một số gạo cho 120 người ăn trong 20 ngày. Sau khi ăn được 5 ngày, bếp ăn nhận thêm 30 người nữa ( Mức ăn của mỗi người như nhau). Hỏi số gạo còn lại đủ ăn trong bao nhiêu ngày nữa ? Có 45 công nhân cùng làm 1 công việc.Họ sẽ hoàn thành công việc đó trong 10 ngày.Sau khi cùng làm được 4 ngày,người ta chuyển bớt đi 15 công nhân để đi làm công việc khác.Hỏi các công nhân còn lại phải làm tiếp trong bao nhiêu ngày nữa thì mới hoàn thành công việc đó? Có 15 công nhân làm 1 công việc dự tính sẽ hoàn thành trong 20 ngày. Cùng làm được 6 ngày, người ta chuyển bớt đi 5 công nhân làm việc ở nơi khác. Hỏi họ còn phải làm trong bao nhiêu ngày mới xong công việc đó?
Xem thêm các dạng bài tập Toán khác :
70 Bài tập về đại lượng tỉ lệ nghịch (có đáp án năm 2023)
60 Bài tập về dãy tỉ số bằng nhau (có đáp án năm 2023)
60 Bài tập về tỉ lệ thức (có đáp án năm 2023)
60 Bài tập làm tròn số và ước lượng (có đáp án năm 2023)
60 Bài tập Tập hợp các số thực (có đáp án năm 2024)