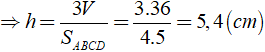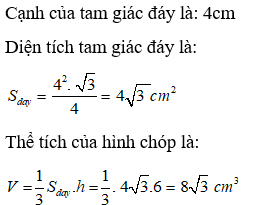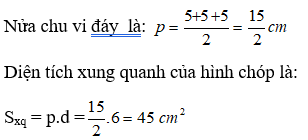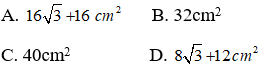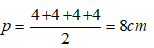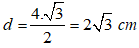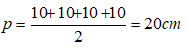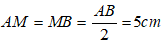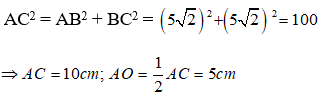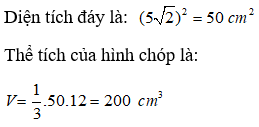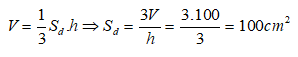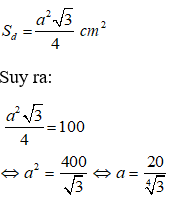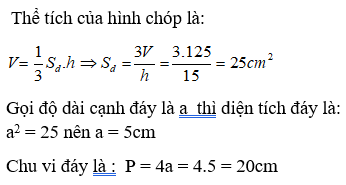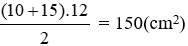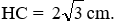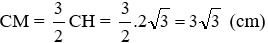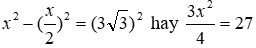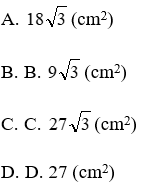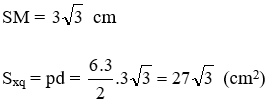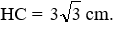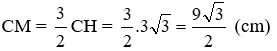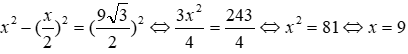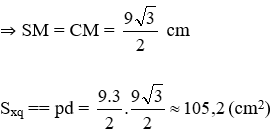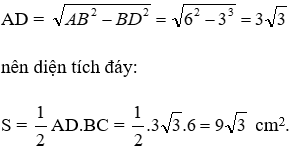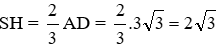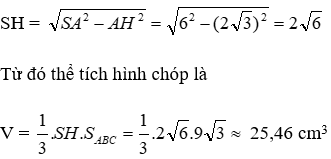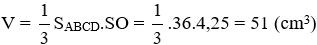20 Bài tập về Hình chóp tứ giác đều (2024) mới nhất, có đáp án

 Hình chóp tứ giác đều

Hình chóp tứ giác đều

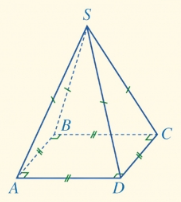
- Hình chóp tứ giác đều S.ABCD;

- Mặt đáy ABCD là một hình vuông;

- Các mặt bên SAB, SBC, SCD, SDA là những tam giác cân tại S;

- Các cạnh đáy AB, BC, CD, DA bằng nhau;

- Các cạnh bên SA, SB, SC, SD bằng nhau;

- Gọi S là đỉnh của hình chóp tứ giác đều S.ABCD.

Chú ý:

Hình chóp tứ giác đều có 5 mặt, 8 cạnh.

Diện tích xung quanh của hình chóp tứ giác đều

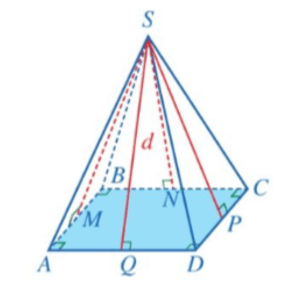
1. Trung đoạn của hình chóp tứ giác đều

Cho hình chóp tứ giác đều S.ABCD. Gọi SM, SN, SP, SQ lần lượt là đường cao của các tam giác SAB, SBC, SCD, SDA. Mỗi đoạn thẳng SM, SN, SP, SQ đều được gọi là trung đoạn của hình chóp tứ giác đều S.ABCD.

2. Công thức tính diện tích xung quanh của hình chóp tứ giác đều

Cách tính:

Diện tích xung quanh của hình chóp tứ giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn.

Tức là:

$S_{xq}=\frac{1}{2}.C.d$, trong đó S_xq là diện tích xung quanh, C là chu vi đáy, d là độ dài trung đoạn của hình chóp tứ giác đều.

Ví dụ:

Tính diện tích xung quanh của hình chóp tứ giác đều biết độ dài cạnh đáy bằng 10 cm và độ dài trung đoạn bằng 7 cm?

Hướng dẫn giải

Chu vi đáy của hình chóp tứ giác đều là: 10 . 4 = 40 (cm).

Diện tích xung quanh của hình chóp tứ giác đều là $S_{xq}=\frac{1}{2}.40.7=140$  (cm²).

Vậy diện tích xung quanh của hình chóp tứ giác đều là 140 cm².

Thể tích của hình chóp tứ giác đều

Cách tính:

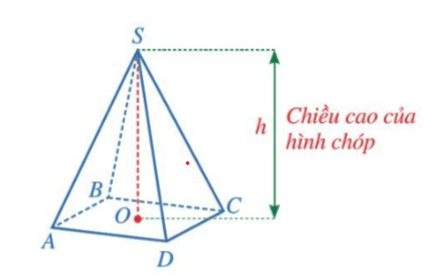
Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với chiều cao.

Tức là:

$V=\frac{1}{3}.S.h$, trong đó V là thể tích, S là diện tích đáy, h là chiều cao của hình chóp tứ giác đều.

Ví dụ:

Tính thể tích của hình chóp tứ giác đều với độ dài cạnh đáy là 8 cm và chiều cao là 9 cm?

Hướng dẫn giải

Diện tích đáy của hình chóp tứ giác đều là: 8.8 = 64 (cm²).

Thể tích hình chóp tứ giác đều là: $V=\frac{1}{3}\mathrm{.64.9}=192$  (cm³).

Vậy thể tích hình chóp tứ giác đều là 192 cm³.

Bài tập Hình chóp tứ giác đều

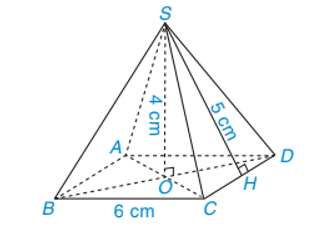
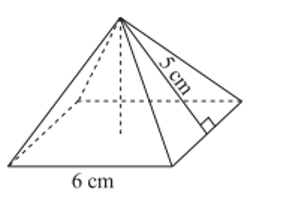
Bài 1: Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 6 cm, độ dài trung đoạn bằng 5 cm và chiều cao bằng 4 cm.

a) Tính diện tích xung quanh của hình chóp tứ giác đều đó?

b) Tính thể tích của hình chóp tứ giác đều đó?

Hướng dẫn giải

a) Chu vi đáy của hình chóp tứ giác đều là: 6 . 4 = 24 (cm).

Diện tích xung quanh của hình chóp tứ giác đều là: $S_{xq}=\frac{1}{2}.24.5=60$  (cm²).

Vậy diện tích xung quanh của hình chóp tứ giác đều là 60 cm².

b) Diện tích đáy của hình chóp tứ giác đều là: 6 . 6 = 36 (cm²).

Thể tích của hình chóp tứ giác đều là: $V=\frac{1}{3}.36.4=48$  (cm³).

Thể tích của hình chóp tứ giác đều là 48 cm³.

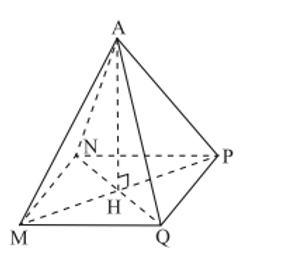
Bài 2: Tính chiều cao AH của hình chóp tứ giác đều A.MNPQ biết độ dài cạnh đáy hình vuông MNPQ là 8cm và thể tích của hình chóp tứ giác đều đó là 192 cm³?

Hướng dẫn giải

Diện tích đáy MNPQ là: S = 8.8 = 64 (cm²).

Độ dài chiều cao AH là: $\frac{3.V_{A.MNPQ}}{S}=\frac{3.192}{64}=9$  (cm).

Vậy độ dài chiều cao AH là 9 cm.

Bài 3: Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy của hình chóp là 6 m, trung đoạn của hình chóp là 5 m. Bác Khôi muốn sơn bốn mặt xung quanh của hộp gỗ. Cứ mỗi mét vuông sơn cần trả 30 000 đồng (tiền sơn và tiền công). Hỏi bác Khôi phải trả chi phí là bao nhiêu?

Hướng dẫn giải

Chu vi đáy của chiếc hộp là: 6.4 = 24 (m).

Diện tích xung quanh của chiếc hộp là: $S_{xq}=\frac{1}{2}\mathrm{.24.5}=60$  (m²).

Diện tích sơn chính là diện tích xung quanh của chiếc hộp.

Do đó số tiền bác Khôi phải trả là: 60. 30 000 = 1 800 000 (đồng).

Vậy số tiền bác Khôi phải trả là 1 800 000 đồng.

Bài tập trắc nghiệm (có đáp án)

Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là?

   A. 6( cm³ )   B. 18( cm³ )

   C. 12( cm³ )   D. 9( cm³ )

Lời giải:

Áp dụng công thức thể tích của hình chóp ta có:

V = 1/3h.S_ABCD = 1/3.2.3² = 6( cm³ )

Chọn đáp án A.

Bài 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 4cm,BC = 5cm. Biết thể tích của hình chóp S.ABCD bằng 36( cm³ ). Tính độ dài đường cao của hình chóp?

   A. 6( cm )   B. 8( cm )

   C. 5,4( cm )   D. 7,2( cm )

Lời giải:

Áp dụng công thức thể tích của hình chóp ta có:

V = 1/3.h.S_ABCD

Chọn đáp án C.

Bài 3: Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng 4cm, các mặt bên là tam giác cân có độ dài cạnh bên là 6cm. Diện tích xung quanh của hình chóp đã cho là?

   A. 32( cm² )   B. 32√ 2 ( cm² )

   C. 16√ 2 ( cm² )   D. 16( cm² )

Lời giải:

Chu vi của đáy ABCD là 2( 4 + 4 ) = 16( cm )

Gọi d là độ dài trung đoạn của hình chóp

Ta có: d = √ (6² - 2²) = 4√ 2 ( cm )

Áp dụng công thức diên tích xung quanh của hình chóp: S_xq = p.d

⇒ S_xq = 8.4√ 2 = 32√ 2 ( cm² )

Chọn đáp án B.

Bài 4: Cho hình chóp tam giác đều có độ dài cạnh đáy là 4cm, chiều cao của hình chóp là 6cm. Tính thể tích của hình chóp là?

   A. 8 cm³     B. 8√3 cm³

   C. 9 cm³     D. 16√3 cm³

Lời giải:

Chọn đáp án B

Bài 5: Cho hình chóp tam giác đều cạnh 5cm và độ dài trung đoạn là 6cm. Tính diện tích xung quanh của hình chóp?

   A. 40cm²     B. 36cm²

   C. 45cm²     D. 50cm²

Lời giải:

Chọn đáp án C

Bài 6: Cho hình chóp tứ giác đều có các mặt bên là tam giác đều cạnh 4cm. Tính diện tích toàn phần của hình chóp?

Lời giải:

Do mặt bên của hình chóp là tam giác đều cạnh 4cm nên đáy là hình vuông cạnh 4cm

Nửa chu vi đáy là

Các mặt bên là tam giác đều cạnh 4cm nên độ dài trung đoạn là

Diện tích xung quanh là:

Chọn đáp án A

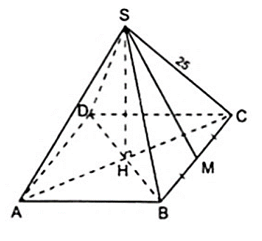
Bài 7: Một hình chóp tứ giác đều S.ABCD có độ dài cạnh bên là 13cm và đáy là hình vuông cạnh 10cm. Tính diện tích xung quanh của hình chóp?

   A. 100cm²     B. 120cm²

   C. 150cm²     D. 240cm²

Lời giải:

Nửa chu vi đáy là:

Gọi M là trung điểm của AB, suy ra:

Áp dụng định lí Pytago vào tam giác vuông SAM có:

SM² = SA² – AM² = 13² – 5² = 144 nên SM = 12cm

Diện tích xung quanh của hình chóp là:

S_xq = p. SM = 20.12 = 240cm²

Chọn đáp án D

Bài 8: Một hình chóp tứ giác đều S.ABCD có cạnh bên SA = 13cm và độ dài cạnh đáy là 5√2. Tính thể tích của hình chóp tứ giác đều.

   A. 200cm³     B. 150cm³

   C. 180cm³     D. 210cm³

Lời giải:

Gọi O là giao điểm của AC và BD.

Áp dụng định lí Pytago vào tam giác vuông ABC có:

Áp dụng định lí Pytago vào tam giác vuông SAO có:

SO² = SA² - AO² = 13² - 5² = 144 nên SO = 12cm

Chọn đáp án A

Bài 9: Cho hình chóp tam giác đều S.ABC có thể tích là 100cm³; chiều cao của hình chóp là 3cm. Tính độ dài cạnh đaý?

   A. 10cm     B. 12cm

   C. 15cm     D. Đáp án khác

Lời giải:

Thể tích của hình chóp đều là:

Gọi độ dài cạnh đáy là a.

Do đáy là tam giác đều nên diện tích đáy là:

Chọn đáp án D

Bài 10: Cho hình chóp tứ giác đều có thể tích là 125cm³, chiều cao của hình chóp là 15cm. Tính chu vi đáy?

   A. 20cm     B. 24cm

   C. 32cm     D. 40cm

Lời giải:

Chọn đáp án A

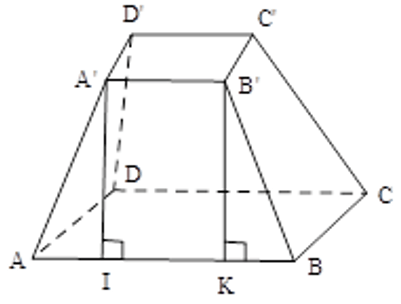
Bài 11: Tính diện tích xung quanh của hình chóp cụt tứ giác đều  có các cạnh đáy  bằng 10cm và 15cm, chiều cao của mặt bên bằng 12cm.

A. 300cm²                  

B. 1200cm²

C. 150cm² 

D. 600cm²

Lời giải

Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên bằng: 

Hình chóp cụt tứ giác đều có 4 mặt bên bằng nhau nên diện tích xung quanh bằng 150.4 = 600 (cm²)

Đáp án cần chọn là: D

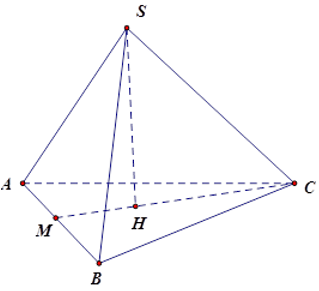
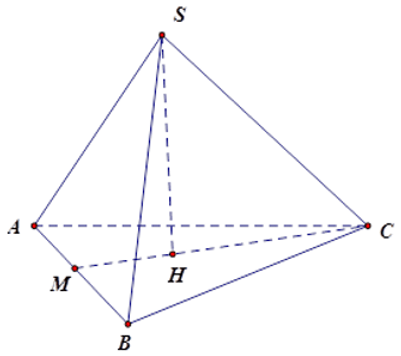
Bài 12: Cho hình chóp tam giác đều S.ABC có các mặt là các tam giác đều. Gọi SH là đường cao của hình chóp, 

1. Tính AB.

A. 2cm

B. 3cm       

C. 6cm       

D. 12cm

Lời giải

Gọi M là giao điểm của CH và AB ta có CM  AB và AM = BM.

Vì H là trọng tâm ΔABC nên: 

Đặt AB = BC = x, ta có BC² - MB² = CM² (định lý Pytago cho ΔMBC) nên

Suy ra x = 6. Vậy BA = 6cm.

Đáp án cần chọn là: C

2. Tính diện tích xung quanh hình chóp

Lời giải

Ta có SM = CM (đường cao hai tam giác đều và bằng nhau) nên:

Đáp án cần chọn là: C

Bài 13: Cho hình chóp tam giác đều S.ABC có các mặt là các tam giác đều. Gọi SH là đường cao của hình chóp, 

1. Độ dài cạnh hình chóp là:

A. 9cm

B. 3cm       

C. 6cm       

D. 12cm

Lời giải

Gọi M là giao điểm của CH và AB ta có CM ⊥ AB và AM = BM. Vì H là trọng tâm ΔABC nên 

Đặt AB = BC = x, ta có BC² - MB² = CM² (định lý Pytago cho ΔMBC) nên

Vậy các cạnh của hình chóp có độ dài là 9cm.

Đáp án cần chọn là: A

2. Tính diện tích xung quanh hình chóp (làm tròn đến một chữ số thập phân)

A. 105(cm²)   

B. 105,2(cm²)

C. 210,4(cm²)

D. 108(cm²)

Lời giải

Xét tam giác SAB và CAB là hai tam giác đều  có cạnh bằng nhau nên SM = CM

Đáp án cần chọn là: B

Bài 14: Tính thể tích của hình chóp tam ggiacs đều có tất cả các cạnh đều bằng 6cm (làm tròn đến chữ số thập phân thứ hai).

A. 24,64cm³   

B. 25,46cm³          

C. 26,46cm³          

D. 26,64cm³

Lời giải

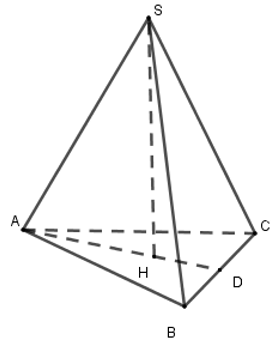
Chóp tam giác đều S.ABC có SH ⊥ (ABC) nên H là trọng tâm tam giác ABC và D là trung điểm BC.

Áp dụng định lý Pytago cho tam giác ABD vuông tại D ta có

Vì H là trọng tâm tam giác ABC ⇒ 

Áp dụng định lý Pytago cho tam giác ASH vuông tại H ta được

Đáp án cần chọn là: B

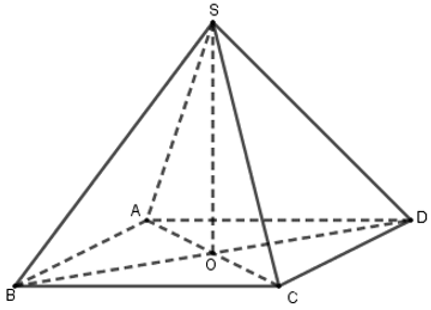
Bài 15: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng 6cm. Thể tích hình chóp gần nhất với số nào dưới đây?

A. 51cm³                    

B. 25cm³   

C. 755cm³ 

D. 65cm³

Lời giải

Diện tích đáy: S_ABCD = 6² = 36(cm²)

Xét tam giác ABC có: AC² = AB² + BC² = 6² + 6² = 72

⇒ AC ≈ 8,5 ⇒ AO = AC = 4,25

Tam giác SOA vuông tại O có: SA² = SO² + OA²

⇔ 6² = SO² + 4,25² ⇔ SO = 4,25

Thể tích hình chóp: 

Đáp án cần chọn là: A

Xem thêm các dạng bài tập liên quan khác:

60 Bài tập về khối đa diện lồi và khối đa diện đều ( có đáp án năm 2023 )

60 Bài tập về mặt cầu (có đáp án năm 2023)

60 Bài tập khái niệm về mặt tròn xoay (có đáp án năm 2023)

60 Bài tập về phương trình mặt phẳng (có đáp án năm 2023)

60 Bài tập về phương trình đường thẳng trong không gian (có đáp án năm 2023)