20 Bài tập về Hình chóp tam giác đều (2024) có đáp án

Hình chóp tam giác đều

Lý thuyết về hình chóp tam giác đều

1. Khái niệm 

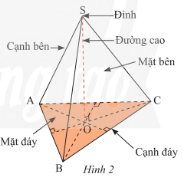
Hình chóp tam giác đều có 4 mặt, 6 cạnh:

- Đáy là tam giác đều.

- 3 cạnh bên bằng nhau.

- 3 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.

- 3 cạnh đáy bằng nhau là ba cạnh của tam giác đáy.

- Chân đường cao trùng với tâm của đáy.

2. Công thức tính diện tích xung quanh

Diện tích xung quanh của hình chóp tam giác đều bằng tổng diện tích của các mặt bên.

Chú ý: Diện tích toàn phần của hình chóp tam giác đều bằng tổng của diện tích xung quanh và diện tích đáy:

S_tp = S_xq + S_đáy

(S_tp là diện tích toàn phần, S_xq là diện tích xung quanh, S_đáy là diện tích đáy).

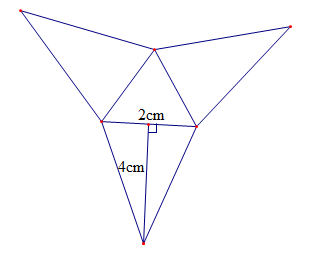
Ví dụ 1. Tính diện tích xung quanh của hình chóp tam giác đều biết độ dài cạnh đáy bằng 2 cm, chiều cao của tam giác mặt bên kẻ từ đỉnh của hình chóp tam giác đều bằng 4 cm.

Hướng dẫn giải

Diện tích xung quanh của hình chóp tam giác đều đã cho là:

$S_{xq}=3.\frac{1}{2}\mathrm{.4.2}=12$ (cm²).

3. Công thức tính thể tích

Thể tích của hình chóp tam giác đều bằng $\frac{1}{3}$ diện tích đáy nhân với chiều cao:

$V=\frac{1}{3}.S_{đáy}.h$

(V là thể tích, S_đáy là diện tích đáy và h là chiều cao).

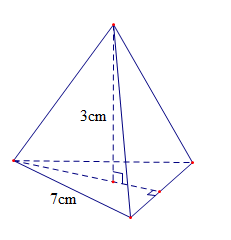
Ví dụ 2. Tính thể tích hình chóp tam giác đều biết chiều cao của hình chóp là 3 cm, tam giác đáy có cạnh bằng 7 cm và chiều cao bằng $\frac{7\sqrt{3}}{2}$ cm.

Hướng dẫn giải

Diện tích đáy của hình chóp tam giác đều là:

${\text{S}}_{đáy}=\frac{1}{2}\mathrm{.7.}\frac{7\sqrt{3}}{2}=\frac{49\sqrt{3}}{4}$ (cm²).

Thể tích hình chóp tam giác đều đã cho là:

$V=\frac{1}{3}.S_{đáy}.h=\frac{1}{3}.\frac{49\sqrt{3}}{4}.3=\frac{49\sqrt{3}}{4}$(cm³).

Bài tập Hình chóp tam giác đều (có đáp án)

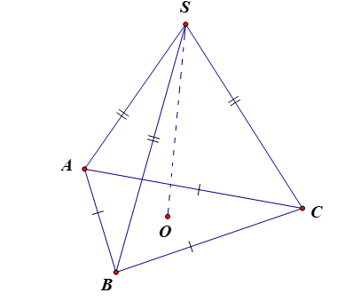
Bài 1: Một hình chóp tam giác đều S.ABC có diện tích đáy ABC là 27 cm² và chiều cao SO là 8cm. Tính thể tích của hình chóp tam giác đều S.ABC?

Hướng dẫn giải

Thể tích của hình chóp tam giác đều đó là: $V=\frac{1}{3}.27.8=72$  (cm³).

Vậy thể tích của hình chóp tam giác đều đó là 72 cm³.

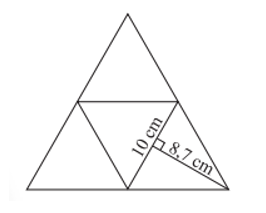
Bài 2: Nhân dịp tết trung thu, Nam dự định làm một chiếc lồng đèn hình chóp tam giác đều. Chiếc đèn lồng được làm bằng một tấm bìa như hình bên dưới biết rằng các mặt đều là hình tam giác đều. Em hãy giúp Nam tính xem phải cần bao nhiêu mét vuông giấy vừa đủ để dán tất cả các mặt của chiếc đèn lồng. Biết rằng nếp gấp không đáng kể? (lấy $\sqrt{3}\approx 1,7$ ).

Hướng dẫn giải

Chu vi đáy của chiếc đèn lồng là: 10.3 = 30 (cm).

Diện tích xung quanh của chiếc đèn lồng là: $S_{xq}=\frac{1}{2}.30.8,7=130,5$  (cm²).

Diện tích mặt đáy của chiếc đèn lồng là: $S={10}^2.\frac{\sqrt{3}}{4}\approx 42,5$  (cm²).

Diện tích giấy dán chiếc đèn lồng là: 130,5 + 42,5 = 173 (cm²).

Vậy diện tích giấy dán chiếc đèn lồng là 173 cm².

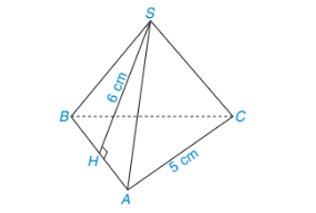
Bài 3: Tính diện tích xung quanh của hình chóp đều S.ABC như hình vẽ bên dưới

Hướng dẫn giải

Nửa chu vi đáy của hình chóp tam giác đều là: $\frac{1}{2}.\left(5+5+5\right)=\frac{15}{2}$  (cm).

Trung đoạn của hình chóp tam giác đều là: d = SH = 6 cm.

Diện tích xung quanh của hình chóp tam giác đều là: $S_{xq}=\frac{15}{2}.6=45$  (cm²).

Vậy diện tích xung quanh của hình chóp tam giác đều là 45 cm².

Bài 4:

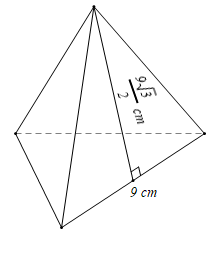
a) Tính diện tích xung quanh và diện tích toàn phần của hình chóp tam giác đều có tất cả các cạnh bằng 9 cm và chiều cao của tam giác mặt bên kẻ từ đỉnh của hình chóp bằng $\frac{9\sqrt{3}}{2}$ cm.

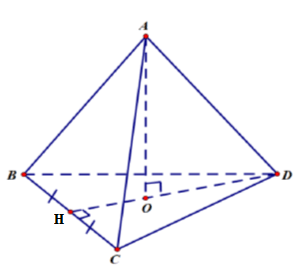
b) Tính thể tích của hình chóp A.BCD sau biết AO = 15 cm, BC = 10 cm, $DH=5\sqrt{3}$ cm.

Hướng dẫn giải

a)

Diện tích xung quanh của hình chóp tam giác đều đã cho là

$S_{xq}=3.\frac{1}{2}\mathrm{.9.}\frac{9\sqrt{3}}{2}=\frac{243\sqrt{3}}{4}$ (cm²).

Do hình chóp tam giác đều này có tất cả các cạnh bằng nhau nên tất cả các mặt là tam giác đều.

Diện tích đáy là

$S_{đáy}\text{=}\frac{1}{2}\mathrm{.9.}\frac{9\sqrt{3}}{2}=\frac{81\sqrt{3}}{4}$(cm²)

Diện tích toàn phần của hình chóp tam giác đều S.ABC là

${\text{S}}_{tp}{\text{= S}}_{xq}\text{+}{S}_{đáy}\text{=}\frac{243\sqrt{3}}{4}+\frac{81\sqrt{3}}{4}=81\sqrt{3}$(cm²).

b) Diện tích đáy là

$S_{đáy}\text{=}\frac{1}{2}\mathrm{.10.5}\sqrt{3}=25\sqrt{3}$(cm²)

Thể tích hình chóp tam giác đều đã cho là:

$V=\frac{1}{3}.S_{đáy}.h=\frac{1}{3}.25\sqrt{3}.15=125\sqrt{3}$(cm³).

Bài 5: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a, cạnh bên tạo với đáy một góc bằng 60 độ. Tính thể tích khối chóp đã cho.

Hướng dẫn giải

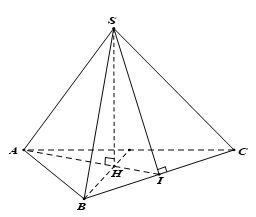
Gọi H là tâm của tam giác ABC. Trong (SBC), kẻ SI vuông góc BC.

Do góc giữa mặt bên và mặt đáy là 60^o suy ra

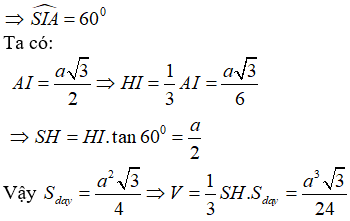
Bài 6: Cho hình chóp đều S.ABC. Chứng minh rằng: Mỗi cạnh bên của hình chóp đó vuông góc với cạnh đối diện, mỗi mặt phẳng chứa một cạnh bên và đường cao của hình chóp đều vuông góc với cạnh đối diện.

Hướng dẫn giải

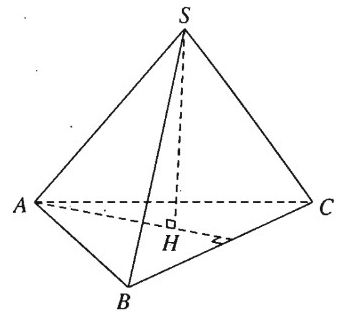
S.ABC là hình chóp đều 

=> △ABC là tam giác đều ⇒ SA = SB = SC.

Do đó khi ta vẽ SH ⊥ (ABC) 

=> H là trọng tâm của △ABC đều và có AH ⊥ BC.

Theo định lý ba đường vuông góc ⇒ SA ⊥ BC

Chứng minh tương tự ta được SB ⊥ AC và SC ⊥ AB.

Vì BC ⊥ AH và BC ⊥ SH ⇒ BC ⊥ (SAH)

Chứng minh tương tự ta có CA ⊥ (SBH) và AB ⊥ (SCH).

Bài 7: Cho hình chóp tam giác đều S_ABC cạnh đáy bằng a và cạnh bên bằng 2a. Chứng minh rằng chân đường cao kẻ từ S của hình chóp là tâm của tam giác đều ABC. Tính thể tích chóp đều S_ABC.

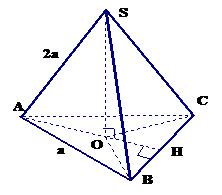
Hướng dẫn giải

Dựng SO⊥ ΔABC, Ta có SA = SB = SC suy ra OA = OB = OC

Vậy O là tâm của tam giác đều ABC.

Ta có :

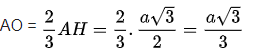
Tam giác ABC đều nên tam giác SAO vuông, áp dụng Pi – ta – go ta có:

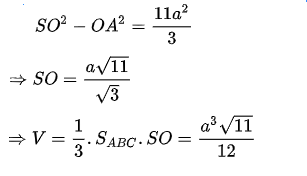
Bài 8: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a, cạnh bên tạo với đáy một góc bằng 60^∘. Tính thể tích khối chóp đã cho.

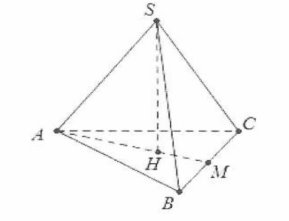
Hướng dẫn giải

Gọi H là trọng tâm tam giác ABC suy ra SH ⊥ (ABC).

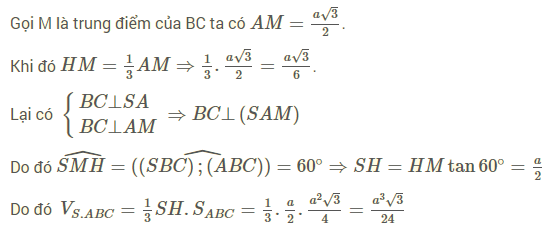
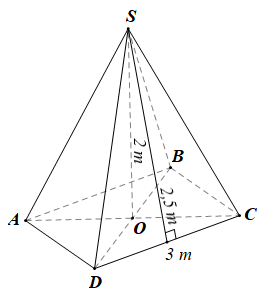
Bài 9: Trong dịp đi cắm trại, các bạn học sinh lớp 8 làm một chiếc lều trại hình chóp tứ giác đều có chiều cao 2 m, đáy là hình vuông cạnh 3 m, chiều cao của mỗi mặt bên của chiếc lều là 2,5 m.

a) Tính thể tích không khí bên trong lều.

b) Tính số mét vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp...).

Hướng dẫn giải

a) Thể tích không khí trong lều bằng thể tích lều và bằng:

$V=\frac{1}{3}.S_{đáy}.h=\frac{1}{3}{.3}^2.2=6$(m³).

b) Số vải bạt cần thiết để dựng lều chính là diện tích xung quanh của lều.

Số mét vải bạt cần thiết để dựng lều là: ${\text{S}}_{xq}=4.\frac{1}{2}\mathrm{.3.2},5=15$ (m²).

Xem thêm các dạng bài tập liên quan khác:

60 Bài tập về khối đa diện lồi và khối đa diện đều ( có đáp án năm 2023 )

60 Bài tập về mặt cầu (có đáp án năm 2023)

60 Bài tập khái niệm về mặt tròn xoay (có đáp án năm 2023)

60 Bài tập về phương trình mặt phẳng (có đáp án năm 2023)

60 Bài tập về phương trình đường thẳng trong không gian (có đáp án năm 2023)