Số gần đúng và sai số
Lý thuyết
1. Số gần đúng
Số a− biểu thị giá trị thực của một đại lượng gọi là số đúng. Số a có giá trị ít nhiều với số đúng a− gọi là số gần đúng của số a−.
2. Sai số tuyệt đối, sai số tương đối
Cho a là số gần đúng của số a−.
Ta gọiΔa=| a− - a| là sai số tuyệt đối của số gần đúng a.
Tỉ số 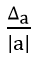
3. Độ chính xác của một số gần đúng.
NếuΔa=| a− - a| ≤ d thì - d ≤ a− - a ≤ d hay - d +a ≤ a− ≤ d + a.
Ta nói a là số gần đúng của a− với độ chính xác d, và quy ước viết gọn là
a−= a ± d.
Nếu biết số gần đúng a và độ chính xác d, ta suy ra số gần đúng nằm trong đoạn [a-d;a+d].
4. Cách viết số quy tròn của số gần đúng căn cứ vào độ chính xác cho trước.
Cho số gần đúng a với độ chính xác d (tức là a−=a ± d). Khi bài toán yêu cầu quy tròn số a mà không nói rõ quy tròn đến hàng nào thì ta quy tròn a đến hàng cao nhất mà d nhỏ hơn một đơn vị của hàng đó.
Ví dụ minh họa
Ví dụ 1:
Giả sử biết số đúng là 8217,3.
Tìm sai số tuyệt đối khi quy tròn số này đến hàng chục.
Lời giải:
Số quy tròn đến hàng chục của x = 8217,3 là 8220.
Sai số tuyệt đối là Δ=|8220 - 8217,3|=2,7.
Ví dụ 2: Một tam giác có ba cạnh đo được như sau:
a=6,3 ± 0,1 cm;b=10 ± 0,2 cm;c=15 ± 0,2 cm
Chứng minh rằng chu vi P của tam giác là P=31,3 ± 0,5 cm.
Lời giải:
Giả sử a=6,3 + u,b=10 + v,c=15 + t.
Ta có: P=a + b + c=31,3 + u + v + t .
Theo giả thiết: - 0,5 ≤ u + v + t ≤ 0,5.
Do đó: P=31 ,3 ± 0,5 cm
Ví dụ 3: Trong một cuộc điều tra dân số, người ta báo cáo số dân của tỉnh A là
a ̅=1718462 ± 150 người. Số quy tròn của a = 1718462 là bao nhiêu?
Lời giải:
Vì độ chính xác đến hàng trăm (d = 150) nên ra quy tròn a đến hàng nghìn. Vậy số quy tròn của a là 1718000.
Bài tập vận dụng (có đáp án)
Bài 1: Chiều dài của một cái cầu là l=1745,25 ± 0,01 m. Hãy cho biết số quy tròn của số gần đúng 1745,25.
Bài 2: giả sử biết số đúng là 3,254. Tìm sai số tuyệt đối khi quy tròn số này đến hàng phần trăm.
Bài 3: Hãy viết số quy tròn của số a với độ chính xác d được cho sau đây:
a) a− = 17658 ± 16;
b) (a)−−−= 15,318 ± 0,056.
Bài 4: Một miếng đất hình chữ nhật có chiều rộng x = 43m ± 0,5m và chiều dài y= 63m ± 0,5m.
Chứng minh rằng chu vi P của miếng đất là P = 212m ± 2m.
Bài 5: Một thửa ruộng hình chữ nhật có chiều dài là x=23m ± 0,01mvà chiều rộng là x=15m ± 0,01m. Tính diện tích S của thửa ruộng đã cho.
Bài 6: Đo độ cao một ngọn cây là h=347,13m ± 0,2m. Hãy viết số quy tròn của số gần đúng 347,13.
Đáp án và hướng dẫn giải
Bài 1: l = 1745 , 25 ± 0,01 m.
Vì độ chính xác đến hàng phần trăm nên ta quy tròn đến hàng phần chục. Vậy số quy tròn của l là 1745,3
Bài 2:
Số quy tròn đến hàng phần trăm là 3,25.
Sai số tuyệt đối là ∆=|3,254-3,25|=0,004
Bài 3:
a) a− = 17658 ± 16;
d = 16 nên ta quy tròn số đến hàng trăm.
Vậy số quy tròn là 17700.
b) (a)−−= 15,318 ± 0,056.
d = 0, 056 nên ta quy tròn số đến hàng phần chục
Vậy số quy tròn là 15, 3.
Bài 4:
Giả sử x = 43 + u, y = 63 + v.
Ta có P = 2x + 2y = 2(43+63) + 2u + 2v = 212 + 2(u + v).
Theo giả thiết -0,5 ≤ u ≤ 0,5 và -0,5 ≤ v ≤ 0,5 nên -2 ≤ 2(u + v) ≤ 2.
Do đó P = 212m ± 2m.
Bài 5:
Ta có: S=x.y=(23 ± 0,01)(15 ± 0,01)
=23.15 ± (23.0,01 + 15.0,01 + 0.012 )=345 ± 0,3801 (m2).
Bài 6:
Ta có độ chính xác d = 0, 2 nên ta quy tròn số đến hàng đơn vị
Số quy tròn là 347 m.
Xem thêm các dạng bài tập khác liên quan:
80 Bài tập các số đặc trưng đo xu thế trung tâm (có đáp án năm 2024)
60 Bài tập hay nhất về Phương sai và Độ lệch chuẩn (có đáp án 2024)
80 Bài tập về Tập hợp và các phép toán trên tập hợp (có đáp án năm 2024)
500 Bài tập Toán 10 Mệnh đề và tập hợp (có đáp án năm 2024)
80 Bài tập các số đặc trưng đo độ phân tán (có đáp án năm 2024)












