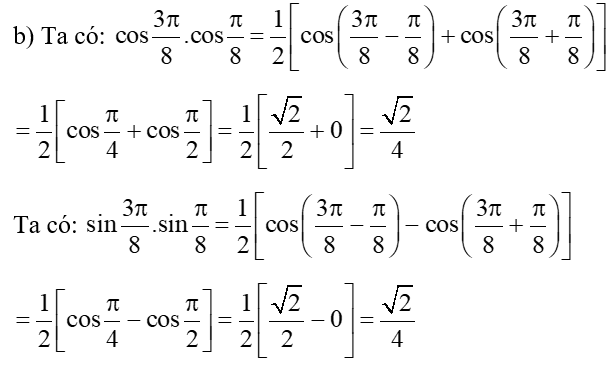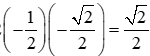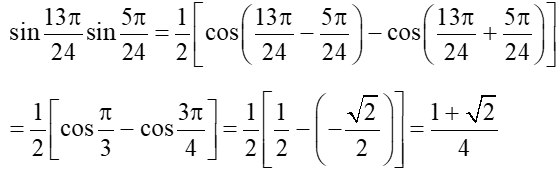Lý thuyết Toán 11 Bài 2: Công thức lượng giác
I. Lý thuyết Công thức lượng giác
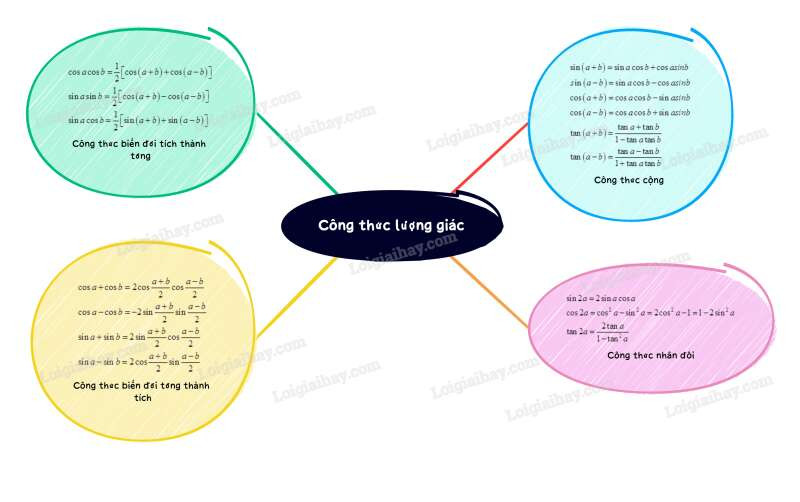
1. Công thức cộng
sin(a+b)=sinacosb+cosasinbsin(a−b)=sinacosb−cosasinbcos(a+b)=cosacosb−sinasinbcos(a−b)=cosacosb+sinasinbtan(a+b)=tana+tanb1−tanatanbtan(a−b)=tana−tanb1+tanatanb
2. Công thức nhân đôi
sin2a=2sinacosacos2a=cos2a−sin2a=2cos2a−1=1−2sin2atan2a=2tana1−tan2a
Suy ra, công thức hạ bậc:
sin2a=1−cos2a2,cos2a=1+cos2a2
3. Công thức biến đổi tích thành tổng
cosacosb=12[cos(a+b)+cos(a−b)]sinasinb=12[cos(a−b)−cos(a+b)]sinacosb=12[sin(a+b)+sin(a−b)]
4. Công thức biến đổi tổng thành tích
cosa+cosb=2cosa+b2cosa−b2cosa−cosb=−2sina+b2sina−b2sina+sinb=2sina+b2cosa−b2sina−sinb=2cosa+b2sina−b2
II. Bài tập Công thức lượng giác
Bài 1. Tính
a) sin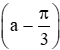
b) cos3π8.cosπ8 + sin3π8.sinπ8.
Hướng dẫn giải
a) Vì 0
Ta có: sin2a + cos2a = 1 ⇒ cos2a = 1 – sin2a = 1-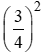
⇒ cosa = √74.
Vậy sin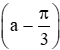
Suy ra: cos3π8.cosπ8+sin3π8.sinπ8=√24+√24=√22.
Bài 2. Tính
a) cos(–15°) + cos255°;
b) sin13π24sin5π24.
Hướng dẫn giải
a) Ta có:
cos(-15o) + cos255o = 2.cos−15°.cos
= 2.cos120o.cos(135o) = 2
Vậy cos(–15°) + cos255° = .
b) Ta có:
Vậy .
Bài 3. Tính sin2a và tan2a biết cos a = và
Hướng dẫn giải
Vì
Ta có:
sin2a + cos2a = 1 ⇒ sin2a = 1 – cos2a = 1 - 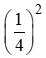
⇒ sina = .
Ta có: sin2a = 2sina cosa = 2.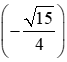
Ta có: tana =
⇒=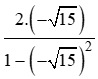
Xem thêm các bài tóm tắt lý thuyết Toán 11 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 1: Giá trị lượng giác của góc lượng giác
Lý thuyết Bài 3: Hàm số lượng giác
Lý thuyết Bài 4: Phương trình lượng giác cơ bản