Trắc nghiệm Ước chung và ước chung lớn nhất có đáp án ( Thông hiểu )
Trắc nghiệm Ước chung và ước chung lớn nhất có đáp án ( Thông hiểu )
-
46 lượt thi
-
6 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Ta phân tích các số đã cho ra thừa số nguyên tố, ta được:
25 = 5 . 5 = 52
45 = 3 . 15 = 3 . 3 . 5 = 32. 5
225 = 9 . 25 = 32. 52
Các thừa số nguyên tố chung là 5, với số mũ nhỏ nhất là 1.
Vậy ƯCLN(25, 45, 225) = 51= 5.
Chọn đáp án D.
Câu 2:
Xem đáp án
Ta đi tìm các ước của 12, 18 và 24:
Các ước của 12 là: 1; 2; 3; 4; 6; 12
Các ước của 18 là: 1; 2; 3; 4; 6; 9; 18
Các ước của 24 là: 1; 2; 3; 4; 6; 8; 12; 24
Suy ra, ƯC(12, 18, 24) = {1; 2; 3; 6}.
Chọn đáp án B.
Câu 3:
Cho a = 32. 5 . 7 và b = 24. 3 . 7. Tìm ƯCLN của a và b.
Xem đáp án
Ta có: a = 32. 5 . 7 và b = 24. 3 . 7
Các thừa số nguyên tố chung của a và b là 3 và 7.
Số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 7 là 1.
Vậy ƯCLN(a, b) = 3 . 7
Chọn đáp án A.
Câu 4:
Xem đáp án
Vì 90 ⁝ a nên a là ước của 90
và 135 ⁝ a nên a là ước của 135
Suy ra a là ước chung của 90 và 135.
Vì a là số lớn nhất thỏa mãn điều kiện trên nên a = ƯCLN (90, 135).
Phân tích các số 90 và 135 ra thừa số nguyên tố, ta được:
90 = 2 . 32. 5
135 = 33. 5
Vậy ƯCLN(90, 135) = 32. 5 = 45 hay a = 45.
Chọn đáp án C.
Câu 5:
Xem đáp án
Vì 18 ⁝ x nên x là ước của 18
và 32 ⁝ x nên x là ước của 32
Suy ra x là ước chung của 18 và 32.
Vì a là số lớn nhất thỏa mãn điều kiện trên nên a = ƯCLN (90, 135).
Phân tích các số 90 và 135 ra thừa số nguyên tố, ta được:
90 = 2 . 32. 5
135 = 33. 5
Vậy ƯCLN(90, 135) = 32. 5 = 45 hay a = 45.
Chọn đáp án C.
Câu 6:
bằng phân số nào sau đây? Xem đáp án
Ta thấy các phân số đã cho ở phần đáp án đều chưa phải là phân số tối giản, do đó ta đi rút gọn các phân số đó.
Để rút gọn các phân số đưa về tối giản, ta chia cả tử và mẫu của phân số đó cho ƯCLN của tử và mẫu.
+) 
Ta có: 20 chia hết cho 10 nên ƯCLN(10, 20) = 10
Nên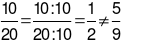 
. Do đó đáp án A sai.
+) 
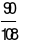
Ta có: ƯCLN(90, 108) = 18
Nên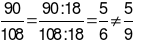 
. Do đó đáp án B sai.
+) 
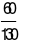
Ta có: ƯCLN(60, 130) = 10
Khi đó: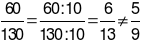 
. Do đó đáp án C sai.
+) 
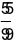
Ta có: ƯCLN(55, 99) = 11
Khi đó: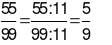 
. Do đó đáp án D đúng.
Chọn đáp án D.