Trắc nghiệm Ước chung và ước chung lớn nhất có đáp án ( Vận dụng )
Trắc nghiệm Ước chung và ước chung lớn nhất có đáp án ( Vận dụng )
-
52 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Các ước của 24là: 1; 2; 22= 4; 23= 8; 2 4= 16
Vậy các ước của 24là 1, 2, 4, 8, 16.
Do đó ta viết tập hợp A: A = {1; 2; 4; 8; 16}.
Chọn đáp án D.
Câu 2:
Xem đáp án
Gọi số tổ có thể chia là a, 
Vì các bác sĩ và y tá được chia đều vào mỗi tổ nên 36 ⁝ a và 108 ⁝ a và a lớn nhất. Do đó, a = ƯCLN(36, 108)
Vì 108 ⁝ 36 nên ƯCLN(36, 108) = 36.
Vậy a = 36 hay có thể chia nhiều nhất thành 36 tổ thỏa mãn yêu cầu bài toán.
Chọn đáp án A.
Câu 3:
Xem đáp án
Lý thuyết: Nếu m = ax. by. cz, với a, b, c là số nguyên tố thì m có (x + 1)(y + 1)(z + 1) ước.
Phân tích số 150 ra thừa số nguyên tố:
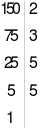
Ta có: 150 = 2 . 3 . 52với x = 1; y = 1; z = 2
Vậy số lượng ước số của 150 là (1 + 1)(1 + 1)(2 + 1) = 12 ước.
Chọn đáp án D.
Câu 4:
Xem đáp án
Gọi chiều dài của viên gạch là x,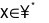 
Để lát kín căn phòng mà không có viên gạch bào bị cắt xén thì x phải là ước của chiều dài và chiều rộng căn phòng.
Hay 680 ⁝ x và 480 ⁝ x
Do đó x là ước chung của 680 và 480, mà x là lớn nhất
Suy ra x = ƯCLN(680, 480)
Ta có: 680 = 23. 5 . 17
480 = 25. 3 . 5
Do đó: ƯCLN(680, 480) = 23. 5 = 8. 5 = 40 hay x = 40 (t/m).
Vậy để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài cạnh viên gạch lớn nhất là 40 cm.
Chọn đáp án D.
Câu 5:
Xem đáp án
Ta có: a = 22. 7 = 4 . 7 = 28
28 = 28 . 1 = 14 . 2 = 7 . 4 = 7 . 2 . 2
Do đó ta tìm được các ước của 28 là: 1, 2, 4, 7, 14, 28.
Vậy Ư(28) = {1; 2; 4; 7; 14; 28}.
Chọn đáp án D.
Câu 6:
Xem đáp án
Gọi a là số hàng dọc nhiều nhất có thể xếp được,
Suy ra 45 ⁝ a, 42 ⁝ a, 48 ⁝ a và a lớn nhất
Do đó, a = ƯCLN(45, 42, 48)
Ta có:
45 = 32. 5
42 = 2 . 3 . 7
48 = 24. 3
Suy ra, ƯCLN(45, 42, 48) = 3 hay a = 3 (t/m).
Vậy số hàng dọc nhiều nhất có thể xếp được là 3 hàng.
Chọn đáp án B.
Câu 7:
Xem đáp án
Lý thuyết: Nếu m = ax. by. cz, với a, b, c là số nguyên tố thì m có (x + 1)(y + 1)(z + 1) ước.
Vậy ta phân tích các số đã cho ra thừa số nguyên tố rồi tìm các ước của số đó.
1 464 = 23. 3 . 61 có (3 + 1)(1 + 1)(1 + 1) = 16 ước
496 = 24. 31 có (4 + 1)(1 + 1) = 10 ước
1 035 = 32. 5 . 23 có (2 + 1)(1 + 1)(1 + 1) = 12 ước
1 517 = 37 . 41 có (1 + 1)(1 + 1) = 4 ước
Vậy số tự nhiên có ước nhiều nhất là 1 464.
Chọn đáp án A.
Câu 8:
Xem đáp án
Gọi số túi mà Hoa chia được là x (túi),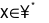 
Vì số bi mỗi màu ở mỗi túi cũng bằng nhau nên 48 ⁝ x, 30 ⁝ x và 60 ⁝ x.
Do đó x là ước chung của 48, 30 và 60
Mà x là lớn nhất nên x = ƯCLN(48, 30, 60)
Ta có: 48 = 24. 3
30 = 2 . 3 . 5
60 = 22. 3 . 5
Do đó: ƯCLN(48, 30, 60) = 2 . 3 = 6 hay x = 6 (t/m).
Vậy Hoa chia được nhiều nhất 6 túi mà mỗi túi có số bi mỗi màu bằng nhau.
Chọn đáp án A.
Câu 9:
Xem đáp án
Ta tính tổng: 1 + 2 + 3 + … + n
Ta thấy tổng trên có: (n – 1) : 1 + 1 = n (số hạng)
Do đó: 1 + 2 + 3 + … + n = n . (n + 1) : 2
Theo đề bài ta được: n . (n + 1) : 2 = 465
Suy ra: n . (n + 1) = 465 . 2 = 930
Nhận thấy tích n . (n + 1) là tích của hai số tự nhiên liên tiếp.
Do đó ta phân tích 930 ra thừa số nguyên tố sau đó phân tích thành tích, ta được:
930 = 2 . 3 . 5 . 31 = (2 . 3 . 5) . 31 = 30 . 31 = 30 . (30 + 1)
Khi đó: n . (n + 1) = 30 . (30 + 1)
Vậy n = 30.
Chọn đáp án D.
Câu 10:
Xem đáp án
Gọi chiều dài viên gạch là x,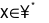
Để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì x phải là ước của chiều dài và chiều rộng căn phòng.
Hay 72 ⁝ x và 56 ⁝ x
Suy ra x là ước chung của 72 và 56.
Mà x là lớn nhất nên x = ƯCLN(72, 56).
Ta có: 72 = 23. 32
56 = 23. 7
Do đó: x = ƯCLN(72, 56) = 23= 8 (t/m).
Vậy để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài viên gạch lớn nhất là 8 dm.
Chọn đáp án A.