Trắc nghiệm Toán 7 Bài 9. Hai đường thẳng song song và dấu hiệu nhận biết có đáp án
Trắc nghiệm Toán 7 Bài 9. Hai đường thẳng song song và dấu hiệu nhận biết có đáp án
-
81 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tia Ot nằm trong góc mOn, \[\widehat {mOt} = \widehat {tOn}\] thì
Xem đáp án
Đáp án đúng là: A
Ot là tia nằm trong góc mOn và tạo với hai cạnh của góc đó hai góc \[\widehat {mOt} = \widehat {tOn}\] nên Ot là tia phân giác của góc mOn.
Do đó chọn đáp án A.
Câu 2:
Nếu đường thẳng z cắt hai đường thẳng x, y và x // y thì ta có :
Xem đáp án
Đáp án đúng là: C
Nếu một đường thẳng cắt hai đường thẳng song song thì:
Hai góc đồng vị bằng nhau;
Hai góc so le trong bằng nhau.
Câu 3:
Cho hình vẽ dưới đây:
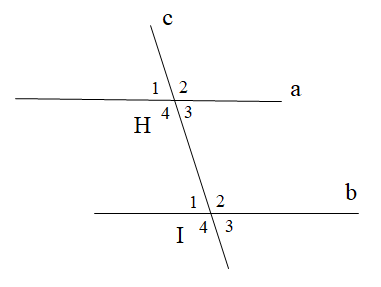
\[\widehat {{H_1}}\] và \[\widehat {{I_1}}\] là hai góc:
Xem đáp án
Đáp án đúng là: D
\[\widehat {{H_1}}\] và \[\widehat {{I_1}}\] là hai góc đồng vị.
Câu 4:
Tính số đo của góc aOb. Biết \[\widehat {zOb} = 48^\circ \], Oz là tia phân giác của góc aOb.
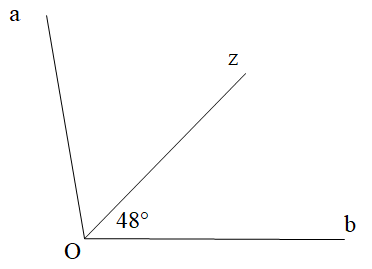
Xem đáp án
Đáp án đúng là: B
Ta có: \[\widehat {aOz} = \widehat {zOb} = 48^\circ \] (vì Oz là tia phân giác góc xOy)
Suy ra \[\widehat {aOb} = \widehat {aOz} + \widehat {zOb} = 48^\circ + 48^\circ = 96^\circ \].
Vậy \[\widehat {aOb} = 96^\circ \].
Câu 5:
Thế nào là tia phân giác của một góc?
Xem đáp án
Đáp án đúng là: D
Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
Câu 6:
Cho \[\widehat {MON} = 90^\circ \] và vẽ tia OP sao cho tia ON là tia phân giác của góc MOP. Khi đó góc MOP là:
Xem đáp án
Đáp án đúng là: B
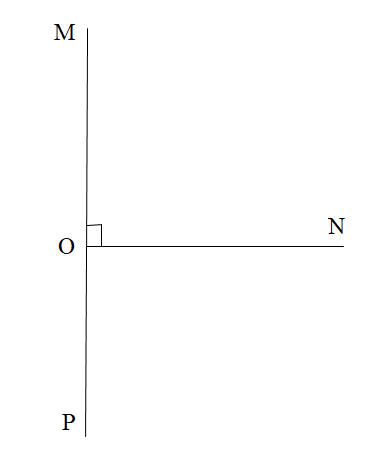
Ta có: ON là tia phân giác của góc MOP nên
\[\widehat {MON} = \widehat {NOP} = 90^\circ \].
Suy ra \[\widehat {MOP} = \widehat {MON} + \widehat {NOP} = 90^\circ + 90^\circ = 180^\circ \].
Vậy góc MOP là góc bẹt.
Câu 7:
Cho hình vẽ
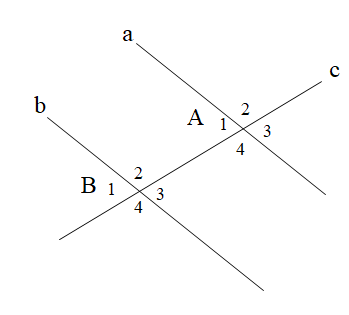
Biết một cặp góc đồng vị \[\widehat {{A_4}} = \widehat {{B_4}} = 60^\circ \]. Tính số đo của cặp góc đồng vị \[\widehat {{A_3}}\] và \[\widehat {{B_3}}\].
Xem đáp án
Đáp án đúng là: A
Ta có:
\[\widehat {{A_4}} + \widehat {{B_3}} = 180^\circ \] (hai góc kề bù)
Do đó \[\widehat {{B_3}} = 180^\circ - 60^\circ = 120^\circ \]
Suy ra \[\widehat {{A_3}}\; = \widehat {{B_3}} = 120^\circ \]
Vậy chọn đáp án A.
Câu 8:
Biết một cặp góc so le trong \[\widehat {{A_4}}\; = \widehat {{B_2}} = 110^\circ \]. Tính số đo của cặp góc so le trong còn lại:
Xem đáp án
Đáp án đúng là: C
Ta có:
\[\widehat {{A_1}} + \widehat {{A_4}} = 180^\circ \] (hai góc kề bù)
\[ \Rightarrow \widehat {{A_1}} = 180^\circ - {110^o} = 70^\circ \]
Mà \[\widehat {{A_4}}\] và \[\widehat {{B_2}}\]; \[\widehat {{A_1}}\] và \[\widehat {{B_3}}\] là hai cặp góc so le trong.
Do đó, \[\widehat {{A_1}} = \widehat {{B_3}} = 70^\circ \]
Vậy số đo của cặp góc so le trong còn lại là \[\widehat {{A_1}} = \widehat {{B_2}} = 70^\circ \].
Câu 9:
Cho hình vẽ
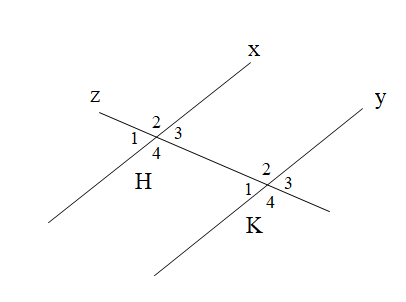
Biết x // y, \[\widehat {{H_3}} = 39^\circ .\]Tính \[\widehat {{H_3}} + \widehat {{K_4}}\].
Xem đáp án
Đáp án đúng là: A
Vì x // y nên suy ra \[\widehat {{H_3}}\] và \[\widehat {{K_3}}\] là hai góc đồng vị \[ \Rightarrow \widehat {{K_3}} = \widehat {{H_3}} = 39^\circ \] (1)
Mà \[\widehat {{K_3}}\] và \(\widehat {{K_4}}\)là hai góc kề bù nên \( \Rightarrow \widehat {{K_3}} + \widehat {{K_4}} = 180^\circ \) (2)
Từ (1) và (2) \( \Rightarrow \widehat {{H_3}} + \widehat {{K_4}} = 180^\circ \)
Vậy \(\widehat {{H_3}} + \widehat {{K_4}} = 180^\circ \)
Câu 10:
Cho hình vẽ
Biết x // y, \[\widehat {{H_3}} = 39^\circ \]. Tính số đo \[\widehat {{K_3}}\]
Xem đáp án
Đáp án đúng là: B
Vì x // y nên \(\widehat {{H_3}} = \widehat {{K_3}}\) ( do \[\widehat {{H_3}}\] và \[\widehat {{K_3}}\] là hai góc đồng vị).
Do đó \[\widehat {{K_3}} = 39^\circ \].
Câu 11:
Chọn hình vẽ. Em hãy chọn câu trả lời đúng.
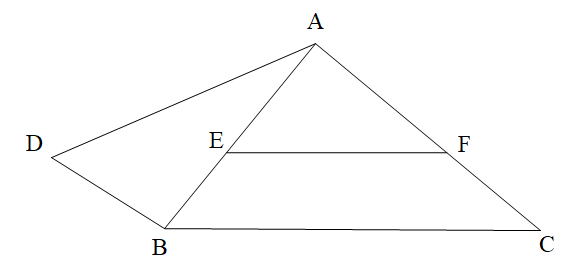
Xem đáp án
Đáp án đúng là: C
\[\widehat {DAB}\] và \[\widehat {EAD}\] là hai góc so le trong là phát biểu sai, vì \[\widehat {DAB}\] và \[\widehat {EAD}\] là hai góc trùng nhau nên loại phương án A.
\[\widehat {AFE}\] và \[\widehat {BAC}\] là hai góc so le trong là phát biểu sai, vì \[\widehat {AFE}\] và \[\widehat {BAC}\] là hai góc trong một tam giác nên loại phương án B.
\[\widehat {AFE}\] và \[\widehat {ACB}\] là hai góc đồng vị là phát biểu đúng nên chọn phương án C;
\[\widehat {BAC}\] và \[\widehat {DAB}\] là hai góc đồng vị là phát biểu sai vì \[\widehat {BAC}\] và \[\widehat {DAB}\] là hai góc kề nhau nên loại phương án D.
Câu 12:
Cho hình vẽ
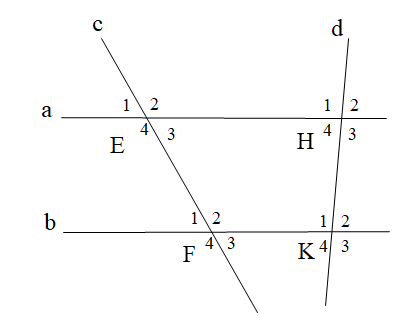
Biết a // b,
\[{\widehat E_1} = 48^\circ \]. Số đo \[\widehat {{F_3}}\] là:
Xem đáp án
Đáp án đúng là: D.
Ta có: \[\widehat {{E_1}}\] và \[\widehat {{F_1}}\] là hai góc đồng vị và a // b nên \[\widehat {{E_1}} = \widehat {{F_1}} = 48^\circ \].
Mà ta lại có \[\widehat {{F_1}}\] và \[\widehat {{F_3}}\] là hai góc đối đỉnh nên \[\widehat {{F_1}} = \widehat {{F_3}}\].
Do đó \[\widehat {{F_3}} = 48^\circ \].
Vậy chọn đáp án D.
Câu 13:
Chọn đáp án đúng.
Nếu đường thẳng c cắt hai đường thẳng a, b và a // b thì:
(I) Hai góc đồng vị bằng nhau
(II) Hai góc so le trong bằng nhau
(III) Hai góc bù nhau bằng nhau
(IV) Hai góc kề bù bằng nhau
Xem đáp án
Đáp án đúng là: A
Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì:
+ Hai góc so le trong bằng nhau.
+ Hai góc đồng vị bằng nhau.
Vậy chọn đáp án A.
Câu 14:
Cho hình vẽ bên dưới. Tính \(\widehat {BEF}\), biết FE // BC và \(\widehat {EBC} = 30^\circ \).
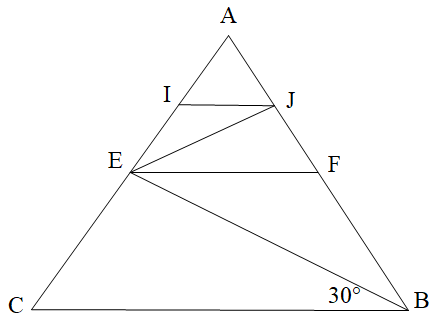
Xem đáp án
Đáp án đúng là: C
Vì FE // BC suy ra \(\widehat {{\rm{BEF}}} = \widehat {EBC} = 30^\circ \) (hai góc so le trong)
Vậy \(\widehat {{\rm{BEF}}} = 30^\circ \).
Câu 15:
Cho \(\widehat {xOy} = 66^\circ \), tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:
Xem đáp án
Đáp án đúng là: A
Ta có Ot là tia phân giác góc xOy \[ \Rightarrow \widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2} = \frac{{66^\circ }}{2} = 33^\circ \].
Vậy chọn đáp án A.