15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 Bài 5. Đường trung trực của một đoạn thẳng có đáp án

Câu 1:

Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.

A. Trung trực;

B. Trung điểm;

C. Trọng tâm;

D. Giao điểm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

Câu 2:

Điền vào chỗ trống sau: “Điểm … hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó”

A. Thuộc;

B. Nằm trên;

C. Cách đều;

D. Nằm trong.

Xem đáp án

Đáp án đúng là: C

Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Câu 3:

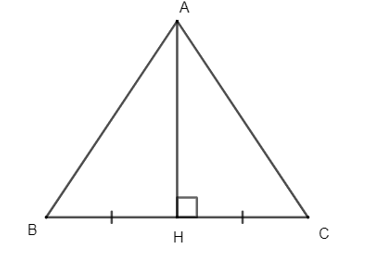
Cho tam giác ABC có AH là đường trung trực của đoạn thẳng BC và H nằm trên đoạn thẳng BC. Cho góc $\hat{B A C} = 70^{o}$ . Tính số đo góc $\hat{A B C}$ .

Cho tam giác ABC có AH là đường trung trực của đoạn thẳng BC và H nằm trên đoạn thẳng (ảnh 1)

A. 60°;

B. 55°;

C. 40°;

D. 50°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Theo đề bài, AH là đường trung trực của BC và H Î BC

Suy ra H là trung điểm của BC

Vì thế HB = HC

Xét ∆AHB và ∆AHC cùng vuông tại H có:

BH = HC (cmt);

AH là cạnh chung.

Do đó ∆AHB = ∆AHC (hai cạnh góc vuông)

Suy ra: AB = AC (hai cạnh tương ứng)

Xét ∆ABC có:

AB = AC (cmt).

Do đó tam giác ∆ABC cân tại A

Suy ra $\hat{A B C}$ = $\hat{A C B}$ (tính chất tam giác cân)

Ta có : $\hat{A B C}$ + $\hat{A C B}$ + = 180° (tổng ba góc của tam giác)

Vì $\hat{A B C}$ = $\hat{A C B}$ (cmt)

Nên $\hat{A B C}$ + $\hat{A B C}$ + $\hat{B A C}$ = 180°.

Khi đó $2 \hat{A B C}$ + 70° = 180°.

Do đó $\hat{A B C}$ = $\frac{180^{o} - 70^{o}}{2}$ = $\frac{110^{o}}{2}$ = 55°.

Vậy số đo góc bằng 55°.

Câu 4:

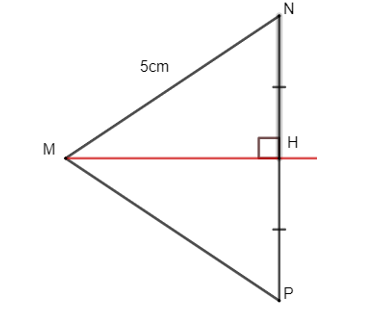
Quan sát hình bên dưới, cho biết H là trung điểm của NP, MH vuông góc với NP tại H và MN = 5 cm. Độ dài của đoạn thẳng MP là:

Quan sát hình bên dưới, cho biết H là trung điểm của NP, MH vuông góc với NP tại H (ảnh 1)

A. 10 cm;

B. 20 cm;

C. 5 cm;

D. 4 cm;

Xem đáp án

Đáp án đúng là: C

Ta có: MH vuông góc với NP tại H;

H là trung điểm của NP.

Do đó MH là đường trung trực của đoạn thẳng NP.

Vì M nằm trên đường trung trực của NP nên cách đều hai đầu mút của đoạn thẳng NP

Nên MN = MP = 5 cm.

Câu 5:

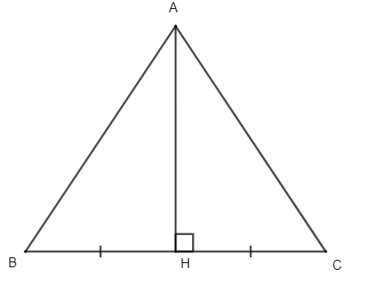
Cho tam giác ABC có AH là đường trung trực của BC và H nằm trên đoạn thẳng BC. Tính số đo góc $\hat{A B C}$ biết số đo góc $\hat{H A C} = 40^{o}$ .

Cho tam giác ABC có AH là đường trung trực của BC và H nằm trên đoạn thẳng BC. (ảnh 1)

A. 60°;

B. 30°;

C. 40°;

D. 50°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ta có: AH là đường trung trực của BC (H Î BC).

Suy ra H là trung điểm của BC.

Do đó HB = HC.

Xét ∆AHB và ∆AHC cùng vuông tại H có:

HB = HC (cmt);

AH là cạnh chung.

Suy ra ∆AHB = ∆AHC (hai cạnh góc vuông).

Do đó AB = AC (hai cạnh tương ứng).

Xét ∆ABC ta có: AB = AC (cmt).

Suy ra ∆ABC là tam giác cân tại A.

Do đó $\hat{A B C}$ = $\hat{A C B}$ .

Ta có : $\hat{A C H}$ + $\hat{H A C}$ = 90° (∆ACH vuông tại H).

$\hat{A C H}$ + 40° = 90°

$\hat{A C B}$ = 50°

Mà $\hat{A B C}$ = $\hat{A C B}$ (cmt)

Nên $\hat{A B C}$ = 50°.

Vậy số đo $\hat{A B C}$ bằng 50°.

Câu 6:

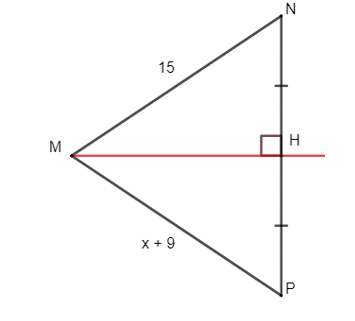
Quan sát hình bên dưới, cho biết MH là đường trung trực của đoạn thẳng NP, cho MN = 15. Vậy x có giá trị là:

Quan sát hình bên dưới, cho biết MH là đường trung trực của đoạn thẳng NP, cho (ảnh 1)

A. 6

B. 15

C. 5

D. 10

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Ta có: MH là đường trung trực của đoạn thẳng NP.

Suy ra MN = MP = 15 (tính chất đường trung trực của đoạn thẳng).

Khi đó MP = x + 9 = 15.

Do đó x = 15 − 9 = 6.

Vậy giá trị của x bằng 6.

Câu 7:

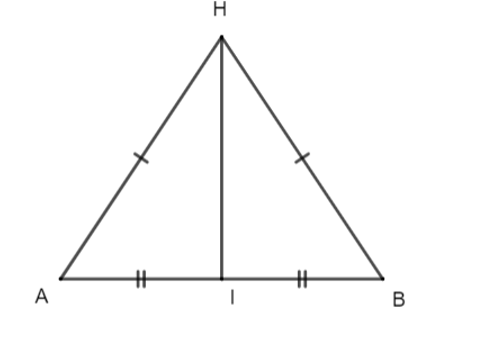
Cho tam giác ∆HAB cân tại H và I là trung điểm của AB (như hình bên dưới). Góc HIB có số đo là:

Cho tam giác ∆HAB cân tại H và I là trung điểm của AB (như hình bên dưới). Góc HIB (ảnh 1)

A. 45°;

B. 90°;

C. 180°;

D. 30°.

Xem đáp án

Đáp án đúng là: B

Xét ∆HIA và ∆HIB có:

AI = IB (I là trung điểm của đoạn thẳng AB);

HA = HB (∆HAB cân tại H);

HI là cạnh chung.

Do đó ∆HIA = ∆HIB (c.c.c)

Suy ra $\hat{H I B}$ = $\hat{H I A}$ (hai góc tương ứng).

mà $\hat{H I B}$ + $\hat{H I A}$ = 180°.

nên $\hat{H I B}$ = 180° : 2 = 90°.

Vậy số đo góc $\hat{H I B}$ = 90°.

Câu 8:

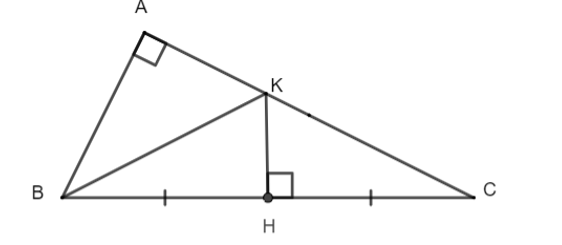
Cho tam giác ABC vuông tại A có $\hat{A B C}$ = 60°, H là trung điểm của BC. Từ H kẻ đường vuông góc với BC cắt AC tại K. Tính $\hat{K B H}$ .

A. 30°;

B. 45°;

C. 60°;

D. 90°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Cho tam giác ABC vuông tại A có góc ABC= 60°, H là trung điểm của BC. Từ H kẻ đường (ảnh 1)

Cho tam giác ABC vuông tại A có góc ABC= 60°, H là trung điểm của BC. Từ H kẻ đường (ảnh 2)

Câu 9:

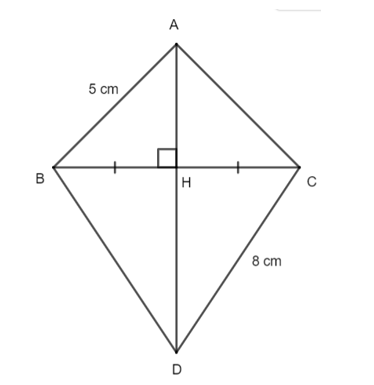
Hình vẽ bên dưới được tạo bởi một đường trung trực qua một đoạn thẳng. Độ dài các cạnh AC và BD là:

Hình vẽ bên dưới được tạo bởi một đường trung trực qua một đoạn thẳng. Độ dài (ảnh 1)

A. AC = 4 cm và BD = 6 cm;

B. AC = 4 cm và BD = 8 cm;

C. AC = 8 cm và BD = 5 cm;

D. AC = 5 cm và BD = 8 cm.

Xem đáp án

Đáp án đúng là: D

Ta có: điểm A nằm trên đường trung trực của BC (hình vẽ).

Suy ra AB = AC = 5 cm (tính chất đường trung trực của đoạn thẳng).

Ta có: D nằm trên đường trung trực của BC (hình vẽ).

Suy ra BD = CD = 8 cm (tính chất đường trung trực của đoạn thẳng).

Vậy độ dài hai cạnh còn lại là AC = 5 cm và BD = 8 cm.

Câu 10:

Cho tam giác ABC vuông tại A và D là trung điểm của AB. Từ D kẻ đường thẳng vuông góc với AB cắt BC tại E.Tính số đo góc $\hat{E A C}$ biết số đo góc $\hat{A B C}$ = 30°.

Cho tam giác ABC vuông tại A và D là trung điểm của AB. Từ D kẻ đường thẳng vuông (ảnh 1)

A. 60°;

B. 90°;

C. 45°;

D. 30°.

Xem đáp án

Cho tam giác ABC vuông tại A và D là trung điểm của AB. Từ D kẻ đường thẳng vuông (ảnh 2)

Câu 11:

Cho tam giác ∆ABC có đường cao AH và H là trung điểm của BC. Vậy tam giác ABC là:

A. Tam giác vuông;

B. Tam giác vuông cân;

C.Tam giác thường;

D.Tam giác cân.

Xem đáp án

Đáp án đúng là: D

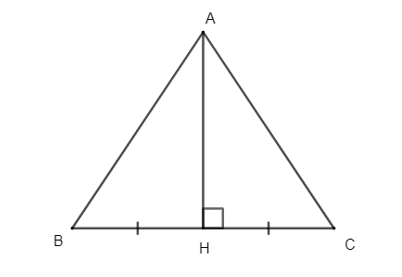
Cho tam giác ∆ABC có đường cao AH và H là trung điểm của BC. Vậy tam giác (ảnh 1)

Ta có: AH vuông góc với BC (H Î BC).

Suy ra AH là đường trung trực của đoạn thẳng BC.

Do đó AB = AC (tính chất đường trung trực của đoạn thẳng).

Xét ∆ABC có: AB = AC.

Suy ra ∆ABC cân tại A.

Vậy tam giác ABC là tam giác cân.

Câu 12:

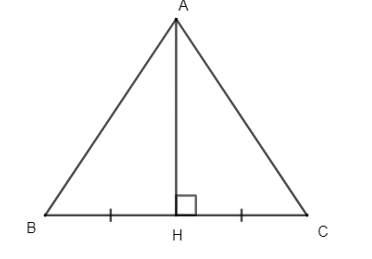
Cho ∆ABC có đường trung trực AH với H thuộc đoạn thẳng BC, cho AH = 5 cm, BC = 8 cm. Diện tích tam giác AHC bằng:

Cho ∆ABC có đường trung trực AH với H thuộc đoạn thẳng BC, cho AH = 5 cm (ảnh 1)

A. 30 cm²;

B. 10 cm²;

C. 15 cm²;

D. 9 cm².

Xem đáp án

Đáp án đúng là: B

Ta có: AH là đường trung trực của BC (H Î BC).

Do đó H là trung điểm của BC.

Suy ra HB = HC = $\frac{B C}{2} = \frac{8}{2}$ = 4 (cm)

Xét ∆AHC vuông tại H, ta có:

S_AHC = $\frac{1}{2}$ . AH . HC = $\frac{1}{2}$ . 5 . 4 = 10 (cm²)

Vậy diện tích tam giác AHC bằng 10 cm².

Câu 13:

Cho tam giác ∆ABC có đường cao AH và H là trung điểm của BC. Cho

\hat{A B C} = 45^{o}

. Vậy tam giác ∆ABC là:

A. Tam giác vuông;

B. Tam giác vuông cân;

C.Tam giác thường;

D.Tam giác cân.

Xem đáp án

Đáp án đúng là: B

Cho tam giác ∆ABC có đường cao AH và H là trung điểm của BC. Cho (ảnh 1)

Cho tam giác ∆ABC có đường cao AH và H là trung điểm của BC. Cho (ảnh 2)

Cho tam giác ∆ABC có đường cao AH và H là trung điểm của BC. Cho (ảnh 3)

Câu 14:

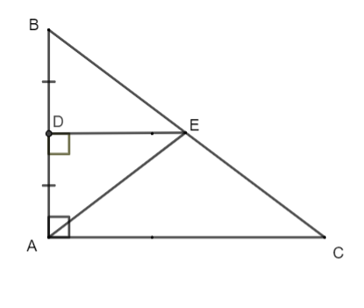
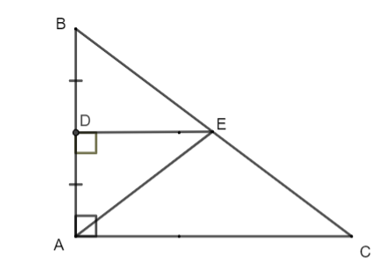
Cho tam giác ABC vuông tại A và D là trung điểm của AB. Từ D kẻ đường thẳng vuông góc với AB cắt BC tại E. Cho AB = 6 cm, AC = 8 cm, DE = 4 cm. Diện tích hình thang DECA là:

A. 18 cm²

B. 30 cm²;

C. 16 cm²;

D. 20 cm².

Xem đáp án

Đáp án đúng là: A

Ta có : AD = BD = $\frac{A B}{2}$ = $\frac{6}{2}$ = 3 (cm) (vì D là trung điểm của đoạn thẳng AB).

Xét hình thang vuông DECA, ta có:

S_DECA = $(\frac{D E + A C}{2})$ . AD = $(\frac{4 + 8}{2})$ . 3

= $\frac{12}{2}$ . 3 = 6 . 3 = 18 (cm²).

Vậy diện tích hình thang DECA là 18 cm².

Câu 15:

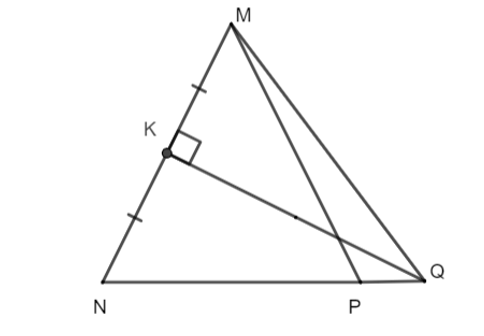
Cho tam giác ΔMNP cân tại M, có $\hat{N M P} = 30^{o}$ , đường trung trực của MN tại trung điểm K của MN cắt NP tại Q. Tính số đo góc $\hat{P M Q}$ .

Cho tam giác ΔMNP cân tại M, có góc MNP=30 độ , đường trung trực của MN tại trung (ảnh 1)

A. 45°;

B. 30°;

C. 50°;

D. 60°.

Xem đáp án

Đáp án đúng là: A

Vì ΔMNP cân tại M (gt).

Nên $\hat{M P N}$ = $\hat{M N P}$ = (180°− $\hat{N M P}$ ) : 2 = (180° − 30°) : 2 = 75°.

Vì Q thuộc đường trung trực của MN.

Nên QM = QN (tính chất đường trung trực của đoạn thẳng).

Xét ΔQMN có:

QM = QN (cmt).

Do đó ΔQMN cân tại Q.

Suy ra $\hat{P M N}$ + $\hat{P M Q}$ = $\hat{Q M N}$ = $\hat{M N Q}$ = 75°.

Khi đó $\hat{P M Q}$ = $\hat{Q M N}$ − $\hat{P M N}$ = 75° − 30° = 45°.

Vậy $\hat{P M Q}$ = 45°.

Trắc nghiệm Toán 7 Bài 5. Đường trung trực của một đoạn thẳng có đáp án

Trắc nghiệm Toán 7 Bài 5. Đường trung trực của một đoạn thẳng có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương