Trắc nghiệm Toán 7 Bài 10. Tiên đề Euclid. Tính chất của hai đường thẳng song song có đáp án
Trắc nghiệm Toán 7 Bài 10. Tiên đề Euclid. Tính chất của hai đường thẳng song song có đáp án
-
229 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Điền nội dung phù hợp vào chỗ trống: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng … với đường thẳng kia.”
Xem đáp án
Đáp án đúng là: A
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
Câu 2:
Ta có a, b phân biệt; nếu a // c và b // c thì:
Xem đáp án
Đáp án đúng là: D
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Câu 3:
Điền cụm từ thích hợp vào chỗ trống: “Nếu một đường thẳng cắt hai đường thẳng … thì hai góc đồng vị bằng nhau.”
Xem đáp án
Đáp án đúng là: A
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Câu 4:
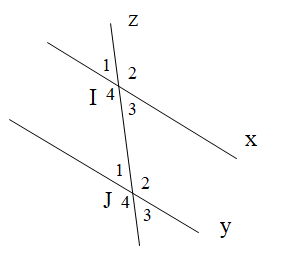
Cho hình vẽ bên dưới. Tính \[\widehat {{I_1}}\], biết \[\widehat {{J_3}} = 26^\circ \]và x // y.
Xem đáp án
Đáp án đúng là: D
Ta có \[\widehat {{I_1}} = \widehat {{I_3}}\] (hai góc đối đỉnh) (1)
Vì x // y nên suy ra \[\widehat {{I_3}} = \widehat {{J_3}}\] (hai góc đồng vị) (2)
Từ (1) và (2) suy ra \[\widehat {{I_1}} = \widehat {{J_3}} = 26^\circ \]
Vậy \[\widehat {{I_1}} = 26^\circ \].
Câu 5:
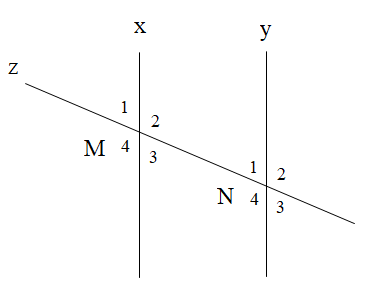
Cho hình vẽ như bên dưới. Tính \[\widehat {{M_3}}\], biết \[\widehat {{N_2}} = 137^\circ \].
Xem đáp án
Đáp án đúng là: B
Ta có \[\widehat {{M_3}}\] và \[\widehat {{N_1}}\] là hai góc so le trong suy ra \[\widehat {{M_3}} = \widehat {{N_1}}\](1)
Lại có \[\widehat {{N_1}}\] và \[\widehat {{N_2}}\] là hai góc kề bù suy ra \[\widehat {{N_1}} + \widehat {{N_2}} = 180^\circ \](2)
Từ (1) và (2) suy ra \[\widehat {{M_3}} + \widehat {{N_2}} = 180^\circ \Rightarrow \widehat {{M_3}} = 180^\circ - 137^\circ = 43^\circ \]
Vậy \[\widehat {{M_3}} = 43^\circ \].
Câu 6:
Nếu đường thẳng t cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì:
Xem đáp án
Đáp án đúng là: C
Nếu đường thẳng t cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì x, y song song với nhau.
Câu 7:
Qua điểm M nằm ngoài đường thẳng a, ta vẽ ba đường thẳng qua M và song song với a thì:
Xem đáp án
Đáp án đúng là: D
Theo tiên đề Euclid ta có: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó
Do đó, qua điểm M nằm ngoài đường thẳng a, ta vẽ ba đường thẳng qua M và song song với a thì ba đường thẳng đó phải trùng nhau.
Vậy chọn đáp án D.
Câu 8:
Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó.
Xem đáp án
Đáp án đúng là: B
Theo tiên đề Euclid ta có: qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Vậy chọn đáp án B.
Câu 9:
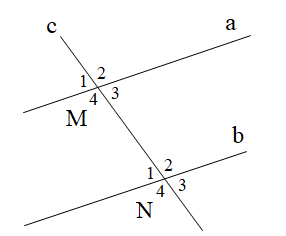
Cho hình vẽ. Nếu a // b thì:
Xem đáp án
Đáp án đúng là: C
Nếu a // b thì \[\widehat {{M_4}}\] và \[\widehat {{N_4}}\] là hai góc đồng vị nên \[\widehat {{M_4}} = \widehat {{N_4}}\].
Vậy chọn phương án C.
Câu 10:
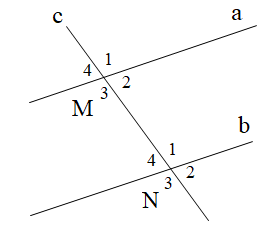
Cho hình vẽ như bên dưới. Tính \[\widehat {{N_3}}\], biết a // b và \[\widehat {{M_1}} = 50^\circ \].
Xem đáp án
Đáp án đúng là: A
Do a // b nên \[\widehat {{M_1}} = \widehat {{N_1}}\] (hai góc đồng vị)
Lại có \[\widehat {{N_1}} = \widehat {{N_3}}\] (hai góc đối đỉnh)
Suy ra \[\widehat {{N_3}} = \widehat {{M_1}} = 50^\circ \].
Do đó \[\widehat {{N_3}} = 50^\circ \].
Vậy chọn đáp án A.
Câu 11:
Cho hai điểm phân biệt H, K. Ta vẽ một đường thẳng x đi qua điểm H và một đường thẳng y đi qua điểm K sao cho x // y. Có thể vẽ được bao nhiêu cặp đường thẳng x, y thỏa mãn điều kiện trên.
Xem đáp án
Đáp án đúng là: D
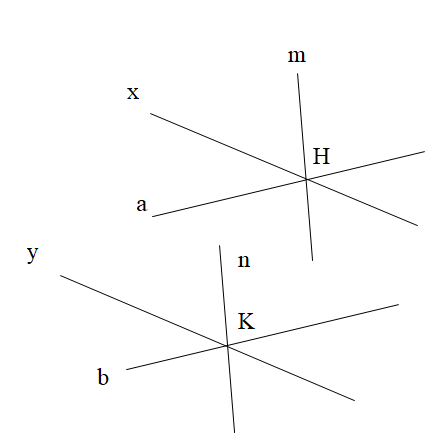
Qua một điểm H cho trước ta có thể vẽ được vô số đường thẳng (ví dụ đường thẳng x, đường thẳng n, đường thẳng i như trên hình vẽ).
Cứ tương ứng với mỗi một đường thẳng đi qua H thì ta vẽ được một đường thẳng đi qua K (theo Tiên đề Euclid) và song song với đường thẳng đi qua H. Trên hình vẽ ta có x // y, m // n, a // b.
Do đó ta vẽ được vô số cặp đường thẳng thoả mãn yêu cầu đề bài.
Vậy chọn đáp án D.
Câu 12:
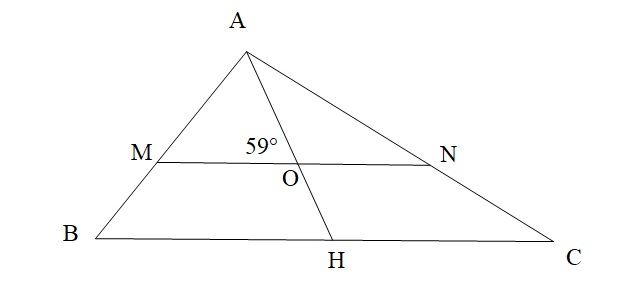
Cho hình vẽ bên dưới. Tính số đo góc OHC, biết MN // BC và \[\widehat {AOM} = 59^\circ \]
Xem đáp án
Đáp án đúng là: B
Do MN // BC nên góc AOM và góc OHB là hai góc đồng vị do đó \[\widehat {AOM} = \widehat {OHB} = 59^\circ \](1).
Lại có, góc OHB và góc OHC là hai góc kề bù nên \[\widehat {OHB} + \widehat {OHC} = 180^\circ \](2).
Từ (1) và (2) suy ra \[\widehat {OHC} = 180^\circ - 59^\circ = 121^\circ \].
Vậy \[\widehat {OHC} = 121^\circ \].
Câu 13:
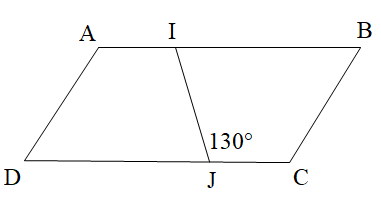
Cho hình bình hành ABCD như hình vẽ. Tính số đo góc AIJ.
Xem đáp án
Đáp án đúng là: D
Ta có: ABCD là hình bình hành suy ra AB // CD
Khi đó góc AIJ và góc IJC là hai góc so le trong nên \[\widehat {AIJ} = \widehat {{\rm{IJ}}C} = 130^\circ \].
Vậy \[\widehat {AIJ} = 130^\circ \].
Vậy chọn đáp án D.
Câu 14:
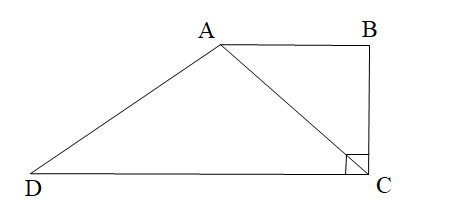
Cho hình thang ABCD như hình vẽ. Tính góc BAC, biết AC là tia phân giác góc BCD.
Xem đáp án
Đáp án đúng là: B
Ta có góc BCD là góc vuông và AC là tia phân giác nên \[ \Rightarrow \widehat {BCA} = \widehat {ACD} = \frac{{\widehat {BCD}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \].
Lại có ABCD là hình thang suy ra AB // CD.
Do góc BAC và góc ACD là hai góc so le trong nên \[\widehat {BAC} = \widehat {ACD} = 45^\circ \].
Vậy số đo của góc BAC là 45°.
Vậy chọn đáp án B.
Câu 15:
Cho hình vẽ bên dưới. Tính góc \[{M_2}\], biết a // b và \[{N_1} = 40^\circ \].
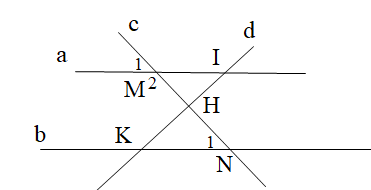
Xem đáp án
Đáp án đúng là: A
Do a // b nên \[\widehat {{M_1}} = \widehat {{N_1}} = 40^\circ \] (hai góc đồng vị) (1)
Lại có \[\widehat {{M_1}}\] và \[\widehat {{M_2}}\] là hai góc kề bù suy ra \[\widehat {{M_1}} + \widehat {{M_2}} = 180^\circ \] (2)
Từ (1) và (2) suy ra \[\widehat {{M_2}} = 180^\circ - 40^\circ = 140^\circ \].
Vậy \[\widehat {{M_2}} = 140^\circ \].
Vậy chọn đáp án A.