Trắc nghiệm Toán 6 KNTT Bài 9: Dấu hiệu chia hết có đáp án
Trắc nghiệm Toán 6 KNTT Bài 9: Dấu hiệu chia hết có đáp án
-
76 lượt thi
-
36 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho các số 27; 82; 195; 234.
Tính tổng các chữ số của mỗi số và xét tính chia hết cho 9 của các tổng đó trong mỗi nhóm.
 Xem đáp án
Xem đáp án
* Xét nhóm các số chia hết cho 9 là: 27; 234
+) Xét số 27 có tổng các chữ số là: 2 + 7 = 9, vì 9 ⁝ 9 nên (2 + 7) ⁝ 9
+) Xét số 234 có tổng các chữ số là: 2 + 3 + 4 = 9, vì 9 ⁝ 9 nên (2 + 3 + 4) ⁝ 9
* Xét nhóm các số không chia hết cho 9 là: 82; 195
+) Xét số 82 có tổng các chữ số là: 8 + 2 = 10, vì 10 9 nên (8 + 2) 9
+) Xét số 195 có tổng các chữ số là: 1 + 9 + 5 = 15, vì 15 9 nên (1 + 9 +5) 9
Câu 2:
Thay dấu * bởi một chữ số để được số chia hết cho 9.
 Xem đáp án
Xem đáp án
Vì số chia hết cho 9 thì tổng các chữ số của nó cũng chia hết cho 9
Nên (1 + 2 + *) chia hết cho 9 hay (3 + *) chia hết cho 9
Vì * là chữ số hàng đơn vị của số nên * ∈ N; 0 ≤ * ≤ 9
Vậy * là 6 ta được số 126.
Câu 3:
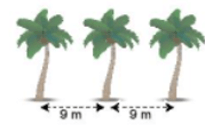
Trên một bờ đất dài 108m, một bác nông dân có kế hoạch trồng một số cây dừa thành một hàng sao cho hai cây cách đều nhau là 9m và luôn có cây ở vị trí đầu và cuối của bờ đất. Hỏi bác nông dân có trồng được như vậy không? Nếu được, bác cần bao nhiêu cây dừa để trồng?
 Xem đáp án
Xem đáp án
Ta thấy 108 có tổng các chữ số là 1 + 0 + 8 = 9 ⁝ 9 nên 108 ⁝ 9
Mà hai cây cách đều nhau 9m vì thế mà bác nông dân trồng được như vậy.
Vì cứ 2 cây dừa liên tiếp có 1 khoảng cách là 9m, 3 cây dừa liên tiếp có 2 khoảng cách,… nên số các khoảng cách giữa hai cây liên tiếp là:
108 : 9 = 12 (khoảng cách)
Số cây dừa bác cần để trồng là:
12 + 1 = 13 (cây)
Vậy bác cần trồng 13 cây dừa.
Câu 4:
Cho các số 42; 80; 191; 234.
Hãy sắp xếp các số trên thành hai nhóm: Nhóm các số chia hết cho 3 và nhóm các số không chia hết cho 3.
 Xem đáp án
Xem đáp án
Ta có: 42 : 3 = 14; 80 : 3 = 26 (dư 2); 191 : 3 = 63 (dư 2); 234 : 3 = 78
+) Các số chia hết cho 3 là: 42; 234
+) Các số không chia hết cho 3 là: 80; 191
Câu 5:
Cho các số 42; 80; 191; 234.
Tính tổng các chữ số của mỗi số và xét tính chia hết cho 3 của các tổng đó trong mỗi nhóm.
 Xem đáp án
Xem đáp án
*Xét nhóm các số chia hết cho 3 là: 42; 234
+) Xét số 42 có tổng các chữ số là: 4 + 2 = 6, vì 6 ⁝ 3 nên (4 + 2) ⁝ 3
+) Xét số 234 có tổng các chữ số là: 2 + 3 + 4 = 9, vì 9 ⁝ 3 nên (2 + 3+ 4 ) ⁝ 3
*Xét nhóm các số không chia hết cho 3 là: 80; 191
+) Xét số 80 có tổng các chữ số là: 8 + 0 = 8, vì 8 3 nên ( 8 +0 ) 3
+) Xét số 191 có tổng các chữ số là: 1 + 9 + 1 = 11, vì 11 3 nên (1 + 9 + 1) 3
Câu 6:
Thay dấu * bằng một chữ số để số chia hết cho 3.
 Xem đáp án
Xem đáp án
Để chia hết cho 3 thì tổng các chữ số của nó cũng chia hết cho 3 nên
(1 + 2 + * + 5) chia hết cho 3 hay (8 + *) chia hết cho 3
Vì * là chữ số ở hàng chục của nên * ∈ N; 0 ≤ * ≤ 9
Do đó: * ∈ {1;4;7}. Khi đó ta có các số: 1 215; 1 245; 1 275
Vậy * ∈ {1;4;7}.
Câu 7:
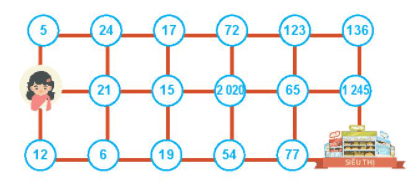
Bạn Hà cần tìm đường đến siêu thị. Biết rằng Hà chỉ có thể đi qua ô có chứa số chia hết cho 2 hoặc chia hết cho 3 và mỗi ô chỉ đi qua một lần. Em hãy giúp Hà đến được siêu thị nhé.
 Xem đáp án
Xem đáp án
Vì Hà chỉ có thể đi qua ô chứa số chia hết cho 2 hoặc 3 nên Hà không thể đi qua các ô số:
5; 17; 19; 65; 77 vì các ô số này đều không chia hết cho 2 và 3.
Có nhiều cách để Hà đi đến siêu thị, dưới đây là 2 cách:
Cách 1: Hà → 21 → 15 → 2020 → 72 → 123 → 136 → 1245 → siêu thị
Cách 2: Hà → 12 → 6 → 21 → 15 → 2020 → 72 → 123 → 136 → 1245 → siêu thị
Câu 8:
Trong các số sau, số nào chia hết cho 2, số nào chia hết cho 5? 324; 248; 2 020; 2025.
 Xem đáp án
Xem đáp án
+) Vì các số 324; 248; 2 020 có chữ số tận cùng lần lượt là 4; 8; 0 nên 324; 248; 2 020 chia hết cho 2
+) Vì các số 2 020; 2025 có chữ số tận cùng lần lượt là 0 và 5 nên 2 020; 2025 chia hết cho 5.
Câu 9:
Trong các số sau, số nào chia hết cho 3, số nào chia hết cho 9?
450 ; 123 ; 2 019 ; 2 025.
 Xem đáp án
Xem đáp án
+) Xét số 450 có tổng các chữ số 4 + 5 + 0 = 9, vì 9 ⁝ 3 và 9 ⁝ 9 nên 450 ⁝ 3 và 450 ⁝ 9.
+) Xét số 123 có tổng các chữ số 1 + 2 + 3 = 6, vì 6 ⁝ 3 và 69 nên 123 ⁝ 3 và 1239
+) Xét số 2 019 có tổng các chữ số 2 + 0 + 1 + 9 = 12, vì 12 ⁝ 3 và 129 nên 2 019 ⁝ 3 và
2 0199
+) Xét số 2 025 có tổng các chữ số 2 + 0 + 2 + 5 = 9, vì 9 ⁝ 3 và 9 ⁝ 9 nên 2 025 ⁝ 3 và 20 25 ⁝ 9
2 025 ⁝ 9.
Vậy các số chia hết cho 3 là: 450; 123; 2 019; 2 025
các số chia hết cho 9 là: 450; 2 025.
Câu 10:
Khối lớp 6 của một trường có 290 học sinh đi dã ngoại. Cô phụ trách muốn chia đều số học sinh của khối 6 thành 9 nhóm. Hỏi cô chia nhóm được như vậy không?
 Xem đáp án
Xem đáp án
Tổng các chữ số của số 290 là 2 + 9 + 0 =11 không chia hết cho 9 nên 290 không chia hết cho 9. Do đó mà cô không thể chia đều 290 học sinh đi dã ngoại thành 9 nhóm.
Vậy không thể chia đều số học sinh của khối 6 thành 9 nhóm.
Câu 11:
Có 162 học sinh tham gia chương trình đào tạo bóng đá, được chia thành các đội. Mỗi đội cần có 9 học sinh. Hỏi có đội nào không đủ 9 học sinh hay không?
 Xem đáp án
Xem đáp án
Tổng các chữ số của 162 là 1 + 6 + 2 = 9 chia hết cho 9 nên 162 chia hết cho 9. Do đó chia 162 em học sinh thành các đội, thì không có đội nào không đủ 9 học sinh.
Câu 12:
Thay dấu * bởi một chữ số để số :
a) Chia hết cho 2
b) Chia hết cho 3
c) Chia hết cho 5
d) Chia hết cho 9.
 Xem đáp án
Xem đáp án
Điều kiện * ∈ N, 0 ≤ * ≤ 9
a) Số chia hết cho 2 thì nó phải có tận cùng là chữ số chẵn nên * ∈ {0;2;4;6;8}
Vậy có thể thay * bằng các chữ số: 0; 2; 4; 6; 8
b) Số chia hết cho 3 thì tổng các chữ số của nó cũng chia hết cho 3.
Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 3.
Mà 12 chia hết cho 3 nên * cũng phải chia hết cho 3 nên * ∈ {0;3;6;9}
Vậy có thể thay * bằng các chữ số: 0; 3; 6; 9
c) Số chia hết cho 5 thì nó phải có tận cùng là 0 hoặc 5 nên * ∈ {0;5}
Vậy có thể thay * bằng các chữ số: 0 ; 5
d) Số chia hết cho 9 thì tổng các chữ số của nó cũng chia hết cho 9
Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 9 nên * ∈ {6}
Vậy có thể thay * bằng chữ số 6.
Câu 13:
Dùng 3 chữ số 3, 0, 4 hãy viết các số tự nhiên có ba chữ số khác nhau và thỏa mãn một trong hai điều kiện:
a) Các số đó chia hết cho 2
b) Các số đó chia hết cho 5
 Xem đáp án
Xem đáp án
a) Vì số cần tìm là số tự nhiên chia hết cho 2 nên số cần tìm có chữ số tận cùng là 0 hoặc 4.
+) Với chữ số tận cùng là 0 và có ba chữ số khác nhau ta được số cần tìm là: 340; 430.
+) Với chữ số tận cùng là 4, chữ số 0 không thể đứng đầu nên số 0 ở hàng chục và số tự nhiên có ba chữ số khác nhau nên ta được số cần tìm là: 304
Vậy các số chia hết cho 2 là: 304; 340; 430.
b) Vì số cần tìm là số tự nhiên chia hết cho 5 nên số cần tìm có chữ số tận cùng là 0.
Vì số tự nhiên có ba chữ số khác nhau nên ta viết được các số: 340; 430
Vậy các số chia hết cho 5: 340; 430.
Câu 14:
Từ các chữ số 5, 0, 4, 2 viết các số tự nhiên có ba chữ số khác nhau sao cho mỗi số đó chia hết cho 3.
 Xem đáp án
Xem đáp án
5 + 4 + 0 = 9
4 + 2 + 0 = 6
Bộ ba chữ số khác nhau có tổng của chúng chia hết cho 3 là: (5; 4; 0) và (4; 2; 0)
+) Với bộ ba chữ số (5; 4; 0) ta được các số tự nhiên có ba chữ số khác nhau là: 504; 540; 405; 450
+) Với bộ ba chữ số (2; 4; 0) ta được các số tự nhiên có ba chữ số khác nhau là: 420; 402; 240; 204.
Vậy các số cần tìm là: 504; 540; 405; 450; 420; 402; 240; 204.
Câu 15:
Cho các số sau: 242; 102; 255; 76; 8 090; 260; 145.
a) Các số chia hết cho 2;
b) Các số chia hết cho 5;
c) Các số chia hết cho cả 2 và 5.
 Xem đáp án
Xem đáp án
a) Các số chia hết cho 2 là các số có chữ số tận cùng là .
Do đó trong các số trên các số chia hết cho 2 là: 242; 102; 76; 8 090; 260.
b) Các số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5.
Do đó trong các số trên số chia hết cho 5 là: 255; 8 090; 260; 145.
c) Các số chia hết cho cả 2 và 5 là: 8 090; 260.
Câu 16:
Trong các số sau: 1 954; 264; 315; 705; 2 231; 3 771 số nào chia hết cho 3, số nào chia hết cho 9.
 Xem đáp án
Xem đáp án
+) Ta có: 1 + 9 + 5 + 4 = 19 không chia hết cho 9 cũng không chia hết cho 3 nên 1954 không chia hết cho 3 và 9.
+) Ta có: 2 + 6 + 4 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 264 chia hết cho 3 và không chia hết cho 9.
+) Ta có: 3 + 1 + 5 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 315 vừa chia hết cho 3 vừa chia hết cho 9.
+) Ta có 7 + 0 + 5 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 705 chia hết cho 3 và không chia hết cho 9.
+) Ta có 2 + 2 + 3 + 1 = 8 không chia hết cho 3 cũng không chia hết cho 9 nên 2 231 không chia hết cho 3 cũng không chia hết cho 9.
+) Ta có: 3 + 7 + 7 + 1 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 3771 vừa chia hết cho 3 vừa chia hết cho 9.
Vậy các số chia hết cho 3 là 264; 315; 705; 3 771; các số chia hết cho 9 là 315; 3 771.
Câu 17:
Khối lớp 6 của một trường có 396 học sinh đi dã ngoại. Cô phụ trách muốn chia đều số học sinh của khối 6 thành 9 nhóm. Hỏi cô chia nhóm được như vậy không?
 Xem đáp án
Xem đáp án
Muốn chia đều số học sinh của khối 6 thành 9 nhóm thì 396 phải chia hết cho 9.
Ta có: 3 + 9 + 6 = 12 + 6 = 18 chia hết cho 9 nên 396 chia hết cho 9.
Do đó cô hoàn toàn có thể chia số học sinh khối 6 thành 9 nhóm.
Câu 18:
Thay dấu * bởi một chữ số để số :
a) Chia hết cho 2;
b) Chia hết cho 3;
c) Chia hết cho 5;
d) Chia hết cho 9.
 Xem đáp án
Xem đáp án
a) Để số đã cho chia hết cho 2 thì * ∈ {2; 4; 6; 8; 0}.
Vậy để số đã cho chia hết cho 2 thì * có thể thay thế bằng các chữ số 2; 4; 6; 8; 0.
b) Ta có: 3 + 1 + 7 + * = 11 + *
Để số đã cho chia hết cho 3 thì 11 + * chia hết cho 3,
Mà * thuộc N
Từ đó, Ta có: 11 + 1 =12 chia hết cho 3;
11 + 4 = 15 chia hết cho 3;
11 + 7 = 18 chia hết cho 3
nghĩa là * ∈ {1; 4; 7}.
Vậy để số đã cho chia hết cho 3 thì * có thể thay thế bằng các chữ số 1; 4; 7.
c) Để số đã cho chia hết cho 5 thì * ∈ {5; 0}.
Vậy để số đã cho chia hết cho 5 thì có thể thay thế * bằng các chữ số 5; 0.
d) Ta có: 3 + 1 + 7 + * = 11 + *
Để số đã cho chia hết cho 9 thì 11 + * chia hết cho 9
Mà * thuộc N
Từ đó, ta có:
11 + 7 = 18 chia hết cho 9.
Vậy để số đã cho chia hết cho 9 ta có thể thay thế * bằng số 7.
Câu 19:
Trong các số sau số nào chia hết cho 2:
 Xem đáp án
Xem đáp án
Đáp án A
Các số chia hết cho 2 là các số có chữ số tận cùng là 0; 2; 4; 6; 8.
Ta thấy 102 có tận cùng bằng 2 nên 102 chia hết cho 2.
Câu 20:
Trong các số: 10 203; 450; 305; 194 724; 234 500. Có bao nhiêu số chia hết cho 5.
 Xem đáp án
Xem đáp án
Đáp án D
Các số chia hết cho 5 có chữ số tận cùng là 0 hoặc 5 là: 450; 305 và 234 500.
Vậy có 3 số chia hết cho 5.
Câu 21:
Trong các số: 102; 355; 270; 2 350; 6 708. Số nào chia hết cho cả 2 và 5.
 Xem đáp án
Xem đáp án
Đáp án C
Số vừa chia hết cho 2 và 5 là số có tận cùng bằng 0.
Câu 22:
Trong các số sau số nào chia hết cho 3: 421; 248; 2 020; 2025.
 Xem đáp án
Xem đáp án
Đáp án D
Ta có 4 + 2 +1 = 7 không chia hết cho 3 nên 421 không chia hết cho 3.
Ta có: 2 + 4 + 8 = 14 không chia hết cho 3 nên 248 không chia hết cho 3.
Ta có 2 + 0 + 2 + 0 = 4 không chia hết cho 3 nên 2 020 không chia hết cho 3.
Ta có: 2 + 0 + 2 +5 = 9 chia hết cho 3 nên 2 025 chia hết cho 3.
Câu 23:
Phát biểu nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án D
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9. Do đó A sai.
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3. Do đó B sai.
Các số có chữ số tận cùng là 0; 2; 4; 6 là các số chia hết cho 2. Do đó C sai.
Các số có chữ số tận cùng là 0 hoặc 5 là các số chia hết cho 5. Do đó D đúng
Câu 24:
Không thực hiện phép tính, em hãy cho biết phát biểu nào là đúng.
 Xem đáp án
Xem đáp án
Đáp án B
Ta có 1 + 9 + 5 + 3 = 18 chia hết cho 9 nên 1 953 chia hết cho 9, nhưng 1 + 9 + 7 + 5 = 22 không chia hết cho 9 nên 1 975 không chia hết cho 9.
Suy ra 1 953 + 1 975 không chia hết cho 9. Do đó A sai.
2 020 và 938 là số có chữ số tận cùng lần lượt là 0 và 8 nên cả hai số đều chia hết cho 2.
Suy ra 2 020 – 938 chia hết cho 2. Do đó B đúng.
Ta có 1 942 có tận cùng là 2 không chia hết cho 5, còn 1 930 có tận cùng là 0 nên chia hết cho 5. Như vậy 1 942 – 1 930 không chia hết cho 5. Do đó C sai.
Ta có 2 + 2 + 2 + 5 = 11 không chia hết cho 3, 1 + 1 + 1 + 3 = 6 chia hết cho 3.
Suy ra 2 225 + 1 113 chia hết cho 3. Do đó D sai.
Câu 25:
Tìm x, y để số vừa chia hết cho 5, vừa chia hết cho 9.
 Xem đáp án
Xem đáp án
Đáp án C
Để số đó chia hết cho 5 thì chữ số tân cùng là 0 hoặc 5.
+) y = 0
Khi đó số đã cho là có tổng các chữ số: 3 + x + 5 + 0 = 8 + x.
Để số này chia hết cho 9 thì 8 + x phải chia hết cho 9.
Suy ra x = 1, x = 10, …
Vì x và y là các chữ số nên x và y thuộc nên x = 1.
Vậy x =1; y = 0.
+) y = 5
Khi đó số đã cho là có tổng các chữ số: 3 + x + 5 + 5 = 13 + x.
Để số này chia hết cho 9 thì 13 + x phải chia hết cho 9.
Suy ra x = 5, x = 14, …
Vì x và y là các chữ số nên x và y thuộc nên x = 5.
Vậy x = 5, y = 5.
Câu 26:
Dùng ba chữ số 3; 0; 4 để viết các số có ba chữ số khác nhau chia hết cho 2. Hỏi có bao nhiêu số như vậy?
 Xem đáp án
Xem đáp án
Đáp án C
Số chia hết cho 2 thì chữ số tận cùng chỉ có thể là 0 hoặc 4.
Nên các số ba chữ số khác nhau lập từ ba chữ số 3; 0; 4 mà chia hết cho 2 là: 304; 340.
Vậy có 2 số như vậy.
Câu 27:
Từ các chữ số 5; 0; 4; 2. Viết các số tự nhiên có ba chữ số khác nhau sao cho mỗi số đó chia hết cho 3.
 Xem đáp án
Xem đáp án
Đáp án D
Ta có: 5 + 0 + 4 = 9 chia hết cho 3 nên các số có ba chữ số khác nhau chia hết cho 3 lập từ ba chữ số này là: 504; 540; 405; 450.
Ta có: 0 + 4 + 2 = 6 chia hết cho 3 nên các số có ba chữ số khác nhau chia hết cho 3 lập từ ba chữ số này là: 402; 420; 240; 204.
Vậy có tất cả 8 số.
Câu 28:
Cho số . Ta có thể thay a bởi bao nhiêu chữ số để số chia hết cho 3.
 Xem đáp án
Xem đáp án
Đáp án C
Ta có: 3 + 2 + a + 3 = 8 + a.
Để số chia hết cho 3 thì 8 + a phải chia hết cho 3.
Suy ra a = 1; a = 4.
Vậy có 2 giá trị của a để số chia hết cho 3.
Câu 29:
Trong các phát biểu dưới đây, có bao nhiêu phát biểu đúng?
I) Số có chữ số tận cùng là 4 thì chia hết cho 2.
II) Số chia hết cho 2 thì có chữ số tận cùng là 4.
III) Số vừa chia hết cho 2 vừa chia hết cho 5 thì có chữ số tận cùng là 0.
IV) Số chia hết cho 5 thì có chữ số tận cùng là 5.
 Xem đáp án
Xem đáp án
Đáp án B
Số có chữ số tận cùng là 4 thì chia hết cho 2. Suy ra (I) đúng.
Số chia hết cho 2 có thể có chữ số tận cùng là các số 0; 2; 4; 6; 8 không nhất thiết là số 4. Suy ra (II) sai.
Số vừa chia hết cho 2 vừa chia hết cho 5 thì có chữ số tận cùng là 0. Suy ra (III) đúng.
Số chia hết cho 5 có chữ số tận cùng là 0 hoặc 5 không chỉ mỗi số 5. Suy ra (IV) sai.
Vậy có 2 phát biểu đúng.
Câu 30:
Trên một bờ đất dài 108m, một bác nông dân có kế hoạch trồng một số cây dừa thành một hàng sao cho hai cây cách đều nhau là 9m và luôn có cây ở vị trí đầu và cuối của bờ đất. Hỏi bác nông dân có trồng được như vậy không? Nếu được, bác cần bao nhiêu cây dừa để trồng?
 Xem đáp án
Xem đáp án
Đáp án B
Ta thấy 108 có tổng các chữ số là 1 + 0 + 8 = 9 9 nên 108 9
Mà hai cây cách đều nhau 9m vì thế mà bác nông dân trồng được như vậy.
Vì cứ 2 cây dừa liên tiếp có 1 khoảng cách là 9m, 3 cây dừa liên tiếp có 2 khoảng cách, … nên số các khoảng cách giữa hai cây liên tiếp là:
108 : 9 = 12 (khoảng cách)
Số cây dừa bác cần để trồng là:
12 + 1 = 13 (cây)
Vậy bác cần trồng 13 cây dừa.
Câu 31:
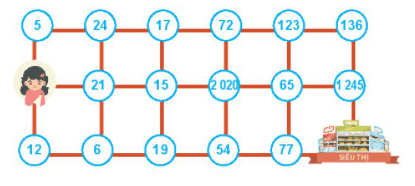
Bạn Hà cần tìm đường đến siêu thị. Biết rằng Hà chỉ có thể đi qua ô có chứa số chia hết cho 2 hoặc chia hết cho 3 và mỗi ô chỉ đi qua một lần. Em hãy giúp Hà đến được siêu thị nhé. Hỏi có mấy cách để Hà đến siêu thị?
 Xem đáp án
Xem đáp án
Đáp án C
Vì Hà chỉ có thể đi qua ô chứa số chia hết cho 2 hoặc 3 nên Hà không thể đi qua các ô số:
5; 17; 19; 65; 77 vì các ô số này đều không chia hết cho 2 và 3.
Có nhiều cách để Hà đi đến siêu thị, dưới đây là 2 cách:
Cách 1: Hà → 21→ 15 → 2020 → 72 → 123 → 136→ 1245 → siêu thị
Cách 2: Hà → 12 → 6 → 21 → 15 → 2020 → 72→ 123 → 136 → 1245 → siêu thị.
Câu 32:
Có 162 học sinh tham gia chương trình đào tạo bóng đá, được chia thành các đội. Mỗi đội cần có 9 học sinh. Nhận xét nào dưới đây là đúng.
 Xem đáp án
Xem đáp án
Đáp án D
Tổng các chữ số của 162 là 1 + 6 + 2 = 9 chia hết cho 9 nên 162 chia hết cho 9. Do đó chia 162 em học sinh thành các đội, thì không có đội nào không đủ 9 học sinh.
Câu 33:
Số 230 có chia hết cho 2 và chia hết cho 5 không?
 Xem đáp án
Xem đáp án
Ta có: 230 : 2 = 115 nên 230 chia hết cho 2
230 : 5 = 46 nên 230 chia hết cho 5
Vậy 230 chia hết cho cả 2 và 5.
Câu 34:
Xét n = (* là chữ số tận cùng của n).
Vận dụng tính chất chia hết của một tổng, hãy cho biết:
a) Thay dấu * bởi chữ số nào thì n chia hết cho 2?
b) Thay dấu * bởi chữ số nào thì n chia hết cho 5?
 Xem đáp án
Xem đáp án
a) n = 230 + * (* là chữ số tận cùng của n,* ∈ N; 0 ≤ * ≤ 9)
Để n ⁝ 2 hay (230+*) ⁝ 2 mà 230 ⁝ 2 nên * ⁝ 2
Lại có 0 ≤ * ≤ 9 do đó * ∈ { 0;2;4;6;8}
b) n = 230 + * (* là chữ số tận cùng của n, * ∈ N; 0 ≤ * ≤ 9)
Để N ⁝ 5 hay (230+*) ⁝ 5 mà 230 ⁝ 5 nên * ⁝ 5
Lại có 0 ≤ * ≤ 9 do đó * ∈ {0;5}.
Câu 35:
(1) Không thực hiện phép tính, em hãy cho biết tổng (hiệu) sau có chia hết cho 2 không.
a) 1 954 + 1 975 b) 2 020 – 938
(2) Không thực hiện phép tính, em hãy cho biết tổng (hiệu) sau có chia hết cho 5 không.
a) 1 945 + 2 020 b) 1 954 – 1 930
 Xem đáp án
Xem đáp án
(1)
a) Số 1 954 có chữ số tận cùng là 4 nên chia hết cho 2; số 1 975 có chữ số tận cùng là 5 nên không chia hết cho 2.
Vậy tổng 1 954 + 1 975 không chia hết cho 2.
b) Số 2 020 có chữ số tận cùng là 0 nên chia hết cho 2; số 938 có chữ số tận cùng là 8 nên chia hết cho 2.
Vậy hiệu 2 020 - 938 chia hết cho 2.
(2)
a) Số 1 945 có chữ số tận cùng là 5 nên chia hết cho 5; số 2 020 có chữ số tận cùng là 0 nên chia hết cho 5.
Vậy tổng 1 945 + 2 020 chia hết cho 5.
b) Số 1 954 có chữ số tận cùng là 4 nên không chia hết cho 5; số 1 930 có chữ số tận cùng là 0 nên chia hết cho 5.
Vậy hiệu 1 954 - 1 930 không chia hết cho 5.
Câu 36:
Cho các số 27; 82; 195; 234.
Hãy sắp xếp các số trên thành hai nhóm: Nhóm các số chia hết cho 9 và nhóm các số không chia hết cho 9.
 Xem đáp án
Xem đáp án
Ta có: 27: 9 = 3; 82 : 9 = 9 (dư 1); 195 : 9 = 21 (dư 6); 234 : 9 = 26
+) Các số chia hết cho 9 là: 27; 234
+) Các số không chia hết cho 9 là: 82; 195
