Trắc nghiệm Toán 6 KNTT Bài 7: Thứ tự thực hiện các phép tính có đáp án
Trắc nghiệm Toán 6 KNTT Bài 7: Thứ tự thực hiện các phép tính có đáp án
-
75 lượt thi
-
30 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Căn hộ nhà bác Cường diện tích 105 . Ngoại trừ bếp và nhà vệ sinh diện tích 30 , toàn bộ diện tích sàn còn lại được lát gỗ như sau: 18 được lát bằng gỗ loại 1 giá 350 nghìn đồng/ , phần còn lại dùng bằng gỗ loại 2 có giá 170 nghìn đồng/ . Công lát là 30 nghìn đồng/
Viết biểu thức tính tổng chi phí bác Cường cần trả để lát sàn căn hộ như trên. Tính giá trị của biểu thức đó.
 Xem đáp án
Xem đáp án
Diện tích sàn được lát gỗ là: 105 - 30 ()
Diện tích sàn lát gỗ loại 2 là: 105 - 30 - 18 ()
Chi phí mua gỗ loại 1 là: 350 000. 18(đồng)
Chi phí mua gỗ loại 2 là: 170 000. (105 - 30 - 18)(đồng)
Chi phí trả công lát gạch là: 30 000. (105 - 30) (đồng)
Biểu thức tính tổng chi phí bác Cường cần trả để lát sàn là:
350 000. 18 + 170 000. (105 - 30 - 18) + 30 000. (105 - 30)
= 6 300 000 + 57. 170 000 + 75 . 30 000
= 6 300 000 + 9 690 000 + 2 250 000
= 15 990 000 + 2 250 000
= 18 240 000 (đồng)
Vậy tổng chi phí bác Cường cần trả để lát sàn căn hộ trên là 18 240 000 đồng.
Câu 2:
Tính giá trị biểu thức sau:
a) 23 + 47 – 52;
b) 24.5:3;
c) .3 + 3.7 – 18:9.
 Xem đáp án
Xem đáp án
a) 23 + 47 – 52
= 70 – 52
= 18.
b) 24.5:3
= 120 : 3
= 40.
c) .3 + 3.7 – 18:9
= 4.3 + 21 – 2
=12 + 21 – 2
= 33 – 2
= 31.
+ Đối với các biểu thức có dấu ngoặc:
- Nếu chỉ có một dấu ngoặc thì ta thực hiện phép tính trong dấu ngoặc trước.
- Nếu có các dấu ngoặc tròn (), dấu ngoặc vuông [], dấu ngoặc nhọn {} thì ta thực hiện các phép tính trong dấu ngoặc tròn trước, rồi thực hiện các phép tính trong dấu ngoặc vuông, cuối cùng thực hiện các phép tính trong dấu ngoặc nhọn.
Câu 3:
Thực hiện phép tính
a) (30 + 80).2 + 20:4;
b) 10 . 2 : 2
 Xem đáp án
Xem đáp án
a) (30 + 80).2 + 20:4
= 110.2 + 5
= 220 + 5
= 225.
b) 10 . 2 : 2
= 20 : 2
= 10.
Câu 4:
Tính giá trị của biểu thức:
a) 36 – 18:6;
b) 2. – 24:(6.2);
c) 120 + [55 – ] + .
 Xem đáp án
Xem đáp án
a) 36 – 18:6 = 36 – 3 = 33
b) 2. – 24:(6.2)
= 2.9 – 24:12
= 18 – 2
= 16
c) 120 + [55 – ] +
= 120 + [55 – ] +
= 120 + [55 – ] +
= 120 + [55 – 25] + 8
= 120 + 30 + 8
= 158.
Câu 5:
Tính giá trị của biểu thức:
a) 1 + 2(a + b) – khi a = 25; b = 9;
b) [2.x – (.4 - 16):y].1230 khi x = 8; y = 1.
 Xem đáp án
Xem đáp án
a) Thay a = 25; b = 9 vào biểu thức ta được:
1 + 2(25 + 9) –
= 1 + 2.34 – 64
= 1 + 68 – 64
= 69 – 64
= 5
b) Thay x = 8, y = 1 vào biểu thức, ta được:
[2.8 – (.4 - 16):1].1230
= [16 – (8.4 - 16):1].1230
= [16 – (32 - 16):1].1230
= [16 – 16:1].1230
= [16 – 16].1230
= 0.1230
= 0
Câu 6:
Phát biểu nào dưới đây là đúng:
 Xem đáp án
Xem đáp án
Đáp án D
Với các biểu thức không có dấu ngoặc: Lũy thừa → Nhân và chia → Cộng và trừ.
Với các biểu thức có dấu ngoặc: trong ngoặc trước, ngoài ngoặc sau: () → [] → {}.
Câu 7:
Cho phép tính 12 + 8.3. Bạn Nam thực hiện như sau:
12 + 8.3
= (12 + 8).3 (Bước 1)
= 20.3 (Bước 2)
= 60. (Bước 3)
Bạn Nam sai từ bước nào?
 Xem đáp án
Xem đáp án
Đáp án A
Bạn Nam sai ngay từ bước 1, vì theo thứ tự thực hiện phép tính phải thực hiện nhân chia trước, cộng trừ sau.
Sửa lại: 12 + 8.3
= 12 + 24
= 36.
Câu 8:
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức không có dấu ngoặc?
 Xem đáp án
Xem đáp án
Đáp án C
Đối với biểu thức không có dấu ngoặc, thứ tự thực hiện phép tính là: Lũy thừa → Nhân và chia → Cộng và trừ.
Câu 9:
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức có dấu ngoặc?
 Xem đáp án
Xem đáp án
Đáp án B
Đối với biểu thức có dấu ngoặc, thứ tự thực hiện phép tính: ( ) → [ ] → { }.
Câu 10:
Hãy chọn biểu thức sử dụng đúng thứ tự các dấu ngoặc:
 Xem đáp án
Xem đáp án
Đáp án A
Biểu thức sử dụng đúng dấu ngoặc là: 100:{2.[30 − (12 + 7)]}.
Câu 12:
21 là kết quả của phép tính nào dưới đây.
 Xem đáp án
Xem đáp án
Đáp án A
+) 60 – [120 – ]
= 60 – [120 – ]
= 60 – [120 – 81]
= 60 – 39
= 21. Do đó A đúng.
+) 60 – [90 – ]
= 60 – [90 – ]
= 60 – [90 – 81]
= 60 – 9
= 51.
+) 25. – 89
= 25.4 – 89
= 100 – 89
= 11.
Câu 13:
Tính giá trị của biểu thức 8.() + 100 tại a = 3, b = 4.
 Xem đáp án
Xem đáp án
Đáp án B
Thay a = 3 và b = 4 vào biểu thức 8.() + 100, ta được:
8.() + 100
= 8.(9 + 16) + 100
= 8.25 + 100
= 200 + 100
= 300.
Câu 15:
Lập biểu thức tính diện tích hình chữ nhật ABCD (hình bên).
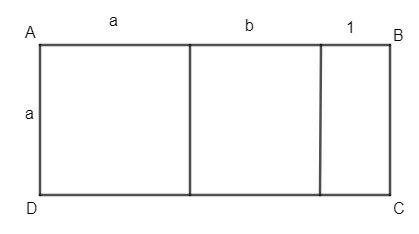
 Xem đáp án
Xem đáp án
Đáp án B
Chiều dài hình chữ nhật là: a + b +1 (đvđd)
Diện tích hình chữ nhật là: (a + b + 1).a = a.a + a.b + a.1 = + ab + 1 (đvdt).
Câu 16:
Có bao nhiêu số tự nhiên n thỏa mãn 32 < 2n 512.
 Xem đáp án
Xem đáp án
Đáp án D
Ta có: 32 < 2n ≤ 512
Mà 32 = 2.2.2.2.2 = ; 512 = 2.2.2.2.2.2.2.2.2 = .
Nghĩa là .
Khi đó: 5 < n ≤ 9, mà n là số tự nhiên nên n ∈ N.
Vậy có tất cả 4 giá trị của n.
Câu 17:
Tính thể tích hình vẽ theo a, b, c.
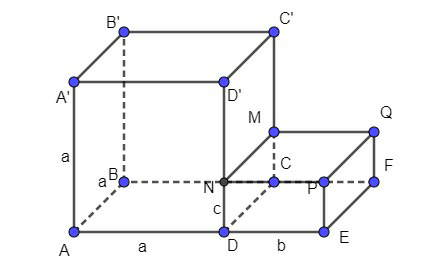
 Xem đáp án
Xem đáp án
Đáp án A
Thể tích khối hộp ABCD.A’B’C’D’ là: (đvtt).
Thể tích khối hộp CDEF.MNPQ là: abc (đvtt).
Thể tích khối hộp cần tìm là: + abc (đvtt).
Câu 18:
Tính thể tích khối hộp ở câu 7 với a = 4, b = 3, c = 1.
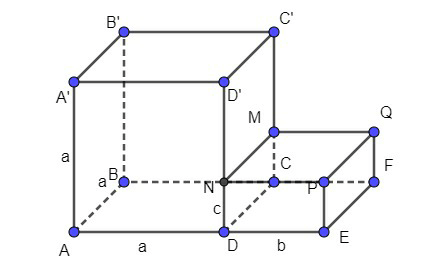
 Xem đáp án
Xem đáp án
Đáp án A
Theo câu 7. Thể tích của hình đã cho là: + abc (đvtt).
Thay a = 4, b = 3 và c = 1 vào biểu thức trên ta được: + 4.3.1 = 64 + 12 = 76 (đvtt).
Câu 19:
Tính giá trị của biểu thức: 120 + [55 – ] + 23.
 Xem đáp án
Xem đáp án
Đáp án D
120 + [55 – ] +
= 120 + [55 – ] + 8
= 120 + [55 – ] + 8
= 120 + [55 – 25] + 8
= 120 + 30 + 8
= 150 + 8
= 158.
Câu 20:
Tính diện tích hình chữ nhật ABCD (hình bên) với a = 10cm, b = 7 cm.
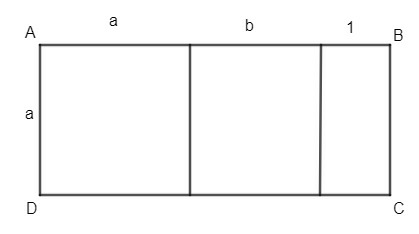
 Xem đáp án
Xem đáp án
Đáp án D
Chiều dài của hình chữ nhật ABCD là: 10 + 7 + 1 = 18 cm.
Diện tích hình chữ nhật ABCD là: 18.10 = 180 .
Câu 21:
Một người đi xe đạp trong 5 giờ. Trong 3 giờ đầu, người đó đi với vận tốc 14km/h; 2 giờ sau, người đó đi với vận tốc 9km/h. Tính quãng đường người đó đi được trong 5 giờ.
 Xem đáp án
Xem đáp án
Đáp án C
Quãng đường người đó đi được trong 3 giờ đầu là:
14. 3 = 42 (km)
Quãng đường người đó đi được trong 2 giờ sau là:
9. 2 = 18 (km)
Quãng đường người đó đi được trong 5 giờ là:
42 + 18 = 60 (km)
Vậy quãng đường người đó đi được trong 5 giờ là 60km.
Câu 22:
Trong 8 tháng đầu năm, một cửa hàng bán được 1 264 chiếc ti vi. Trong 4 tháng cuối năm, trung bình mỗi tháng cửa hàng bán được 164 chiếc ti vi. Hỏi trong cả năm, trung bình mỗi tháng cửa hàng đó bán được bao nhiêu ti vi? Viết biểu thức tính kết quả.
 Xem đáp án
Xem đáp án
Đáp án D
Số ti vi 4 tháng cuối năm cửa hàng đó bán được là:
164 . 4 = 656 (chiếc)
Tổng số ti vi cả năm cửa hàng đó bán được là:
656 + 1 264 = 1 920 (chiếc)
Vì cả năm có 12 tháng
Trong cả năm, trung bình mỗi tháng cửa hàng bán được số ti vi là:
1 920 : 12 = 160 (chiếc)
Vậy trong cả năm, trung bình mỗi tháng cửa hàng bán được 160 chiếc ti vi.
Câu 23:
Căn hộ nhà bác Cường diện tích 105. Ngoại trừ bếp và nhà vệ sinh diện tích 30, toàn bộ diện tích sàn còn lại được lát gỗ như sau: 18 được lát bằng gỗ loại 1 giá 350 nghìn đồng/, phần còn lại dùng bằng gỗ loại 2 có giá 170 nghìn đồng/. Công lát là 30 nghìn đồng/
Viết biểu thức tính tổng chi phí bác Cường cần trả để lát sàn căn hộ như trên. Tính giá trị của biểu thức đó.
 Xem đáp án
Xem đáp án
Đáp án C
Diện tích sàn được lát gỗ là: 105 – 30 = 75 ()
Diện tích sàn lát gỗ loại 2 là: 75 – 18 = 57 ()
Chi phí mua gỗ loại 1 là: 350 000. 18 = 6 300 000 (đồng)
Chi phí mua gỗ loại 2 là: 170 000. 57 = 9 690 000 (đồng)
Chi phí trả công lát gạch là: 30 000. 75 = 2 250 000 (đồng)
Biểu thức tính tổng chi phí bác Cường cần trả để lát sàn là:
6 300 000 + 9 690 000 + 2 250 000
= 15 990 000 + 2 250 000
= 18 240 000 (đồng)
Vậy tổng chi phí bác Cường cần trả để lát sàn căn hộ trên là 18 240 000 đồng.
Câu 24:
Trong tình huống mở đầu, bạn nào làm đúng quy ước trên?

 Xem đáp án
Xem đáp án
Với biểu thức 5 + 3 x 2 bằng mấy?
Vì biểu thức trên có phép tính cộng và nhân thì ta thực hiện nhân trước rồi đến cộng.
Do đó: 5 + 3 x 2 = 5 + 6 = 11
Vậy bạn Vuông xanh làm đúng theo quy ước trên.
Câu 25:
Tính giá trị của các biểu thức sau:
a) 25. – + 125.
b) 2. + 5.(2 + 3).
 Xem đáp án
Xem đáp án
a) 25. – + 125 = 25.8 – 9 + 125 = 200 - 9 + 125 = 191 + 125 =316;
b) 2. + 5.(2+3) = 2.9 + 5.5 = 18 + 25 = 43.
Câu 26:
Một người đi xe đạp trong 5 giờ. Trong 3 giờ đầu, người đó đi với vận tốc 14km/h; 2 giờ sau, người đó đi với vận tốc 9km/h.
a) Tính quãng đường người đó đi được trong 3 giờ đầu; trong 2 giờ sau.
b) Tính quãng đường người đó đi được trong 5 giờ.
 Xem đáp án
Xem đáp án
a) Quãng đường người đó đi được trong 3 giờ đầu là:
14. 3 = 42 (km)
Quãng đường người đó đi được trong 2 giờ sau là:
9. 2 = 18 (km)
b) Quãng đường người đó đi được trong 5 giờ là:
42 + 18 = 60 (km)
Vậy:
a) Quãng đường người đó đi trong 3 giờ đầu và 2 giờ sau lần lượt là 42km, 18 km.
b) Quãng đường người đó đi được trong 5 giờ là 60km.
Câu 27:
a) Lập biểu thức tính diện tích của hình chữ nhật ABCD (hình dưới).
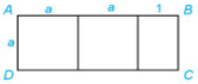
b) Tính diện tích của hình chữ nhật đó khi a = 3cm.
 Xem đáp án
Xem đáp án
a) Độ dài đoạn thẳng AB là:
a + a + 1 = 2.a + 1 (đơn vị độ dài)
Diện tích hình chữ nhật ABCD là:
AB . AD = a . (2.a + 1) (đơn vị diện tích)
b) Khi a = 3cm thì diện tích hình chữ nhật là:
3. (2.3 + 1) = 3 . 7 = 21 ()
Vậy: Diện tích hình chữ nhật ABCD là a . (2.a + 1) đơn vị diện tích.
Diện tích hình chữ nhật khi a = 3 cm là 21 .
Câu 28:
Tính:
a) 235 + 78 - 142;
b) 14 + 2 . ;
c) {+ [1 + ]}:13.
 Xem đáp án
Xem đáp án
a) 235 + 78 - 142 = 313 – 142 = 171
b) 14 + 2 . = 14 + 2 . 64 = 14 + 128 = 142
c) {+ [1 + ]} : 13 = [8 + (1 + )] : 13 = [8 + (1 + 4)] : 13
= (8 + 5) : 13 = 13 : 13 = 1
Câu 29:
Tính giá trị của biểu thức:
1 + 2(a + b) – khi a = 25; b = 9.
 Xem đáp án
Xem đáp án
Thay a = 25; b = 9 vào biểu thức 1 + 2(a + b) - ta được:
1 + 2(a + b) - = 1 + 2. (25 + 9) - = 1 + 2.34 – 64 = 1 + 68 – 64 = 69 – 64 = 5
Vậy 1 + 2(a + b) - = 5 khi a = 25; b = 9.
Câu 30:
Trong 8 tháng đầu năm, một cửa hàng bán được 1 264 chiếc ti vi. Trong 4 tháng cuối năm, trung bình mỗi tháng cửa hàng bán được 164 chiếc ti vi. Hỏi trong cả năm, trung bình mỗi tháng cửa hàng đó bán được bao nhiêu ti vi? Viết biểu thức tính kết quả.
 Xem đáp án
Xem đáp án
Số ti vi 4 tháng cuối năm cửa hàng đó bán được là:
164 . 4 = 656 (chiếc)
Tổng số ti vi cả năm cửa hàng đó bán được là:
656 + 1 264 = 1 920 (chiếc)
Vì cả năm có 12 tháng
Trong cả năm, trung bình mỗi tháng cửa hàng bán được số ti vi là:
1 920 : 12 = 160 (chiếc)
Vậy trong cả năm, trung bình mỗi tháng cửa hàng bán được 160 chiếc ti vi.
Từ lời giải trên, ta có biểu thức để tính kết quả trung bình mỗi tháng trong cả năm, cửa hàng bán được số ti vi là: (1 264 + 164 . 4) : 12
Tính giá trị của biểu thức như sau:
(1 264 + 164 . 4) : 12
= (1 264 + 656) : 12
= 1 920 : 12 = 160
Vậy trong cả năm, trung bình mỗi tháng cửa hàng bán được 160 chiếc ti vi.
