Dạng 2: Nhận biết và chứng minh hai đường thẳng vuông góc có đáp án
-
157 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hai tam giác cân ABC và DBC có chung cạnh đáy BC nằm trong hai mặt phẳng khác nhau. Khẳng định nào sau đây là đúng nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
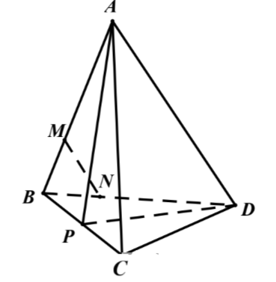
Gọi P là trung điểm của BC.
Vì các tam giác ABC và DBC cân nên:
AP vuông góc với BC
DP vuông góc với BC
Ta có: .
Vậy BC vuông góc với ADCâu 2:
Cho hình chóp S.ABC có SA = SB = SC và . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
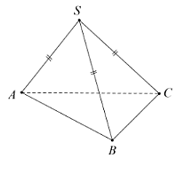
Ta có:
Vậy SA vuông góc với BC.
Câu 3:
Cho hình lập phương ABCD.A1B1C1D1. Chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
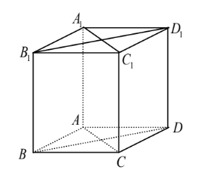
Ta có:
(sử dụng các vectơ bằng nhau và tính chất hình bình hành)
Vậy góc giữa AA1 và B1D1 bằng .
Câu 4:
Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Theo lí thuyết ta có: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Câu 5:
Cho hai tam giác cân ABC và DBC có chung cạnh đáy BC nằm trong hai mặt phẳng khác nhau. Gọi M, N là các điểm lần lượt thuộc các đường thẳng AB và DB sao cho , . Hai đường thẳng MN và BC có quan hệ:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
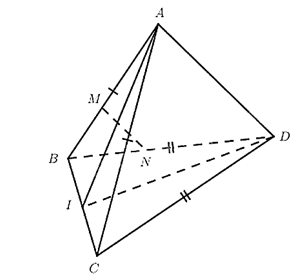
Ta có , , suy ra .
Từ đó suy ra MN // AD (định lí Thalès đảo trong tam giác ABD). (1)
Gọi I là trung điểm của BC, thì các tam giác ABC và DBC cân nên:
AI vuông góc với BC
DI vuông góc với BC
Ta có:
Do đó, BC vuông góc với AD. (2)
Từ (1) và (2) suy ra BC và MN vuông góc với nhau.
Câu 6:
Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AC, BC, BD, DA. Khẳng định nào sau đây là đúng nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
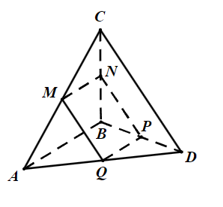
Đặt AB = AD = AC = a.
Ta có:
Do đó, AB vuông góc với CD.
Dễ thấy MN, PQ lần lượt là đường trung bình của các tam giác ABC và ABD.
Khi đó, MN // PQ // AB và MN = PQ = = nên tứ giác MNPQ là hình bình hành
Lại có:
MN // AB
NP // CD (do NP là đường trung bình của tam giác BCD)
AB ⊥ CD
Khi đó, MN ⊥ NP.
Do đó, MNPQ là hình chữ nhật.
Câu 7:
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN, SC) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
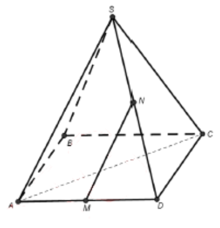
Ta có: AC =
⇒ AC2 = 2a2 = SA2 + SC2
Do đó tam giác SAC vuông tại S.
Khi đó:
Do đó, MN vuông góc với SC hay .
Câu 8:
Cho tứ diện ABCD có AB = AC = AD và , . Gọi I, J lần lượt là trung điểm của AB và CD. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
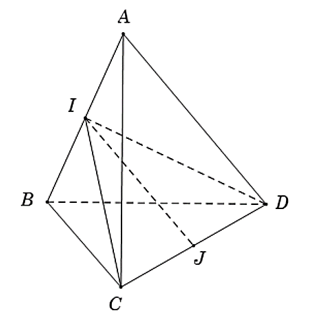
Xét tam giác ICD có J là trung điểm đoạn CD
Do đó:
Tam giác ABC có AB = AC và nên tam giác ABC đều
Do đó, CI vuông góc với AB (1).
Tương tự, ta có tam giác ABD đều nên DI vuông góc với AB (2).
Từ (1) và (2) có:
.
Do đó, IJ vuông góc với AB.
Câu 9:
Trong không gian cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Nếu a // b và c ⊥ a thì c ⊥ b.
Câu 10:
Cho bài toán sau:
Cho tứ diện ABCD. Chứng minh rằng nếu: thì AB vuông góc với CD, AC vuông góc với BD, AD vuông góc với BC. Điều ngược lại đúng không?
Sau đây là lời giải
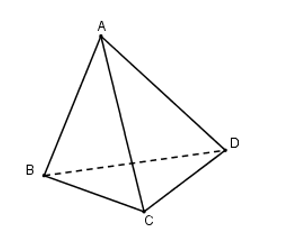
Bước 1:
Do đó, AC vuông góc với BD.
Bước 2: Chứng minh tương tự, từ ta được AD vuông góc với BC và ta được AB vuông góc với CD.
Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1, bước 2 là quá trình biến đổi tương đương.
Hướng giải trên đúng hay sai? Nếu sai thì sai ở đâu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Hướng giải trên là đúng.
