Trắc nghiệm Toán 10 Bài tập cuối chương 6 có đáp án
Trắc nghiệm Toán 10 Bài tập cuối chương 6 có đáp án
-
142 lượt thi
-
30 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Tập xác định của hàm số \[y = \frac{{x - 1}}{{{x^2} - x + 3}}\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[{x^2} - x + 3 = {\left( {x - \frac{1}{2}} \right)^2} + \frac{{11}}{4} > 0{\rm{ }}\forall x \in \mathbb{R}\].
Vậy hàm số có tập xác định D = ℝ.
Câu 2:
Cho hàm số có đồ thị như hình vẽ

Kết luận nào sau đây là đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Quan sát đồ thị hàm số, ta thấy:
Đồ thị ta có hàm số đi lên trên khoảng (– ∞; 1) và đi xuống trên khoảng (1; + ∞) nên hàm số đồng biến trên khoảng (– ∞; 1) và nghịch biến trên khoảng (1; + ∞).
Vậy đáp án đúng là C.
Câu 3:
Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
 Xem đáp án
Xem đáp án
Đáp án đúng là : A
Tọa độ đỉnh \[I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\]
Ta có \[ - \frac{b}{{2a}} = - \frac{8}{{2.1}} = - 4\]; \[ - \frac{\Delta }{{4a}} = - \frac{{{8^2} - 4.1.12}}{{4.1}} = - 4\]
Vậy tọa độ đỉnh I(– 4; – 4)
Câu 4:
Đồ thị hàm số y = – 9x2 + 6x – 1 có dạng là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Giao điểm của đồ thị hàm số với trục tung là điểm A(0; – 1) vậy giao điểm có tung độ âm nên loại đáp án A.
Trục đối xứng của đồ thị hàm số \[x = - \frac{b}{{2a}} = - \frac{6}{{2.( - 9)}} = \frac{1}{3}\] vậy trục đối xứng nằm về phần dương của trục Ox nên loại đáp án C và D.
Vậy đáp án đúng là B.
Câu 5:
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét f(x) = x2 – 1 có ∆ = – 4.(–1) = 4 > 0, a = 1 > 0 và có hai nghiệm phân biệt x1 = –1 và x2 = 1.
Khi đó ta có bảng xét dấu:
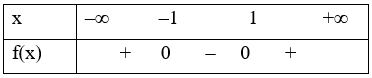
Từ bảng xét dấu ta có f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞); f(x) < 0 khi x ∈ (– 1; 1)
Vậy khẳng định sai là D
Câu 6:
Tam thức f(x) = x2 – 2x – 3 nhận giá trị dương khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét f(x) = x2 – 2x – 3 có ∆’ = (–1)2 – 1(–3) = 4 > 0 và a = 1 > 0 nên hàm số có hai nghiệm phân biệt x1 = –1 và x2 = 3.
Khi đó, ta có bảng xét dấu:
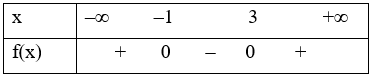
Suy ra f(x) > 0 với x ∈ (– ∞; – 1) \( \cup \) (3; + ∞); f(x) < 0 khi x ∈ (– 1; 3)
Vậy f(x) nhận giá trị dương khi x ∈ (– ∞; – 1) \( \cup \) (3; + ∞).
Câu 7:
Cho parabol (P): y = ax2 + bx + 1. Xác định (P) biết rằng parabol đi qua hai điểm A(1; 4) và B(– 1; 2).
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì parabol đi qua A(1; 4) ta có 4 = a + b + 1
Parabol qua B(– 1; 2) ta có 2 = a – b + 1
Khi đó ta có hệ phương trình: \[\left\{ \begin{array}{l}a + b = 3\\a - b = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 1\end{array} \right.\]
Vậy parabol cần tìm là: y = 2x2 + x + 1.
Câu 8:
Nghiệm của phương trình \[\sqrt {2x - 3} = x - 3\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Điều kiện của phương trình 2x – 3 ≥ 0 \[ \Leftrightarrow x \ge \frac{3}{2}\]
Ta có \[\sqrt {2x - 3} = x - 3 \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\2x - 3 = {(x - 3)^2}\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} - 8x + 12 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 2\\x = 6\end{array} \right.\end{array} \right. \Leftrightarrow x = 6\]
Câu 9:
Số nghiệm của phương trình \[\sqrt {{x^2} - 3x} = \sqrt {2x - 4} \]
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Điều kiện của phương trình \[\left\{ \begin{array}{l}{x^2} - 3x \ge 0\\2x - 4 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \le 0\\x \ge 3\end{array} \right.\\x \ge 2\end{array} \right. \Leftrightarrow x \ge 3\]
Xét phương trình:\[\sqrt {{x^2} - 3x} = \sqrt {2x - 4} \]
\[ \Leftrightarrow {x^2} - 3x = 2x - 4\]
\[ \Leftrightarrow {x^2} - 5x + 4 = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\]
Ta thấy x = 1 (không thỏa mãn điều kiện), x = 4 (thỏa mãn điều kiện).
Vậy phương trình có 1 nghiệm x = 4.
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Điều kiện xác định \[\left\{ \begin{array}{l}x - 2 \ge 0\\x - 6 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \ne 6\end{array} \right.\]
Vậy tập xác định của hàm số là D = [2; 6) \[ \cup \] (6; + ∞).
Câu 11:
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
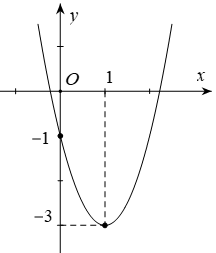
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Dựa vào đồ thị ta có trục đối xứng x = 1
Đáp án A, B đều có trục đối xứng x = 1 nên A, B đều thỏa mãn
Đáp án C có trục đối xứng x = 2 nên loại đáp án C.
Đáp án D có trục đối xứng \[x = \frac{1}{4}\] nên loại đáp án D.
Dựa vào đồ thị ta có tọa độ đỉnh I(1; – 3)
Đáp án A có tọa độ đỉnh I(1; – 3) đáp án A thỏa mãn.
Đáp án B có tọa độ đỉnh I(1; – 2) nên loại đáp án B.
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có a = 1 > 0; b = – 2; c = – 1.
Vì a = 1 > 0 nên
Hàm số đồng biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) hay (1; + ∞). Đáp án A đúng
Hàm số nghịch biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\) hay (– ∞; 1). Đáp án C đúng
Tọa độ đỉnh xI = \( - \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1\) và yI = \( - \frac{\Delta }{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{{( - 2)}^2} - 4.1.( - 1)}}{{4.1}} = - 2\).
Vậy toạ độ đỉnh I(1; - 2)
Đáp án D đúng
Đồ thị hàm số có trục đối xứng là \[x = - \frac{b}{{2a}} = 1\]. Đáp án B sai
Câu 13:
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x ∈ ℝ.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trường hợp 1. m = 0. Khi đó f(x) = – 2x – 1 < 0 \[ \Leftrightarrow x > - \frac{1}{2}\]
Vậy m = 0 không thỏa mãn f(x) < 0 với \[\forall x \in \mathbb{R}\]
Trường hợp 2. m ≠ 0.
Khi đó: f(x) = mx2 – 2x – 1 < 0 với \[\forall x \in \mathbb{R}\]\[ \Leftrightarrow \left\{ \begin{array}{l}a = m < 0\\\Delta ' = 1 + m < 0\end{array} \right. \Leftrightarrow m < - 1\]
Vậy m < – 1 thỏa mãn bài toán.
Câu 14:
Tổng các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Điều kiện của phương trình: x2 – 2x – 3 ≥ 0 \[ \Leftrightarrow \left[ \begin{array}{l}x \ge 3\\x \le - 1\end{array} \right.\]
\[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7 \Leftrightarrow {x^2} - 2x - 3 + 3\sqrt {{x^2} - 2x - 3} - 4 = 0\]
Đặt \[\sqrt {{x^2} - 2x - 3} = t(t \ge 0)\] ta có phương trình t2 + 3t – 4 =0\[ \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = - 4\end{array} \right.\]
Kết hợp với điều kiện của t ta thấy t = 1 thỏa mãn
Với t = 1 \[ \Rightarrow \sqrt {{x^2} - 2x - 3} = 1 \Leftrightarrow {x^2} - 2x - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 + \sqrt 5 \\x = 1 - \sqrt 5 \end{array} \right.\]
Kết hợp với điều kiện của x thì \[x = 1 + \sqrt 5 ;x = 1 - \sqrt 5 \] đều thỏa mãn
Vậy tổng các nghiệm của phương trình S = 2.
Câu 15:
Nghiệm của phương trình \[\sqrt {x - 2} + \sqrt {x + 3} = 5\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Điều kiện của phương trình: \[\left\{ \begin{array}{l}x - 2 \ge 0\\x + 3 \ge 0\end{array} \right. \Leftrightarrow x \ge 2\]
\[\sqrt {x - 2} + \sqrt {x + 3} = 5\]
\[ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x - 2 + x + 3 + 2\sqrt {(x - 2)(x + 3)} = 25\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\sqrt {{x^2} + x - 6} = 12 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 \le x \le 12\\{x^2} + x - 6 = {x^2} - 24x + 144\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}2 \le x \le 12\\25x - 150 = 0\end{array} \right. \Leftrightarrow x = 6\].
Câu 16:
Hàm số y = – x2 + 2x + 1 đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tọa độ đỉnh của hàm số là I(1; 2)
Bảng biến thiên
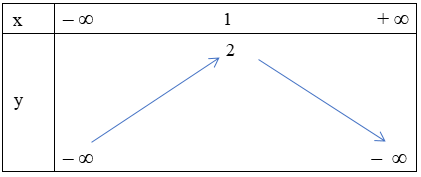
Từ bảng biến thiên ta có hàm số tăng từ trái sang phải trên khoảng (– ∞; 1) nên hàm số đồng biến trên khoảng (– ∞; 1).
Câu 17:
Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng \(\forall x \ge 3\)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: a = 2 > 0. Do đó, 2x2 – 4x + m + 5 > 0, \(\forall x \ge 3\) sẽ có trường hợp sau:
Trường hợp 1. ∆ < 0 \( \Leftrightarrow \) (– 4)2 – 4.2.(m + 5) < 0 \( \Leftrightarrow \) m > – 3, khi đó
2x2 – 4x + m + 5 > 0 với \(\forall x \in \mathbb{R}\).
Do đó 2x2 – 4x + m + 5 > 0 với \(\forall x \ge 3\).
Trường hợp 2. ∆ ≥ 0, khi đó phương trình 2x2 – 4x + m + 5 = 0 sẽ có hai nghiệm x1; x2.
Do đó, để 2x2 – 4x + m + 5 > 0, \(\forall x \ge 3\)\[ \Leftrightarrow \left\{ \begin{array}{l}\Delta \ge 0\\{x_1} \le {x_2} < 3\end{array} \right.\]
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta \ge 0\\a\,f\left( 3 \right) > 0\\\frac{S}{2} < 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \le - 3\\2\left( {{{2.3}^2} - 4.3 + m + 5} \right) > 0\\1 < 3\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \le - 3\\m > - 11\end{array} \right.\)\( \Leftrightarrow \). – 11 < m ≤ – 3
Kết hợp hai trường hợp lại ta được m > – 11 thì thì 2x2 – 4x + m + 5 > 0 với \(\forall x \ge 3\).
Câu 18:
Tập ngiệm của bất phương trình: x(x + 5) ≤ 2(x2 + 2) là:
 Xem đáp án
Xem đáp án
Đáp án đúng: A
Ta có: x(x + 5) ≤ 2(x2 + 2) \( \Leftrightarrow \)x2 – 5x + 4 ≥ 0
Đặt f(x) = x2 – 5x + 4 ta có f(x) = 0 \( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\).
Ta có bảng xét dấu :
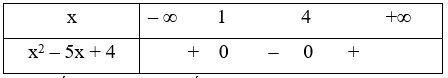
Dựa vào bảng xét dấu nghiệm của bất phương trình \[x \in (--\infty ;1] \cup [4; + \infty )\]
Câu 19:
Bất phương trình: \[\left( {{x^2} - 3x - 4} \right).\sqrt {{x^2} - 5} < 0\] có bao nhiêu nghiệm nguyên dương?
 Xem đáp án
Xem đáp án
Ta có điều kiện: x2 – 5 ≥ 0\[ \Leftrightarrow \left[ \begin{array}{l}x \le - \sqrt 5 \,\\x \ge \sqrt 5 \end{array} \right.\].
Vậy \[\left( {{x^2} - 3x - 4} \right).\sqrt {{x^2} - 5} < 0\]\[ \Leftrightarrow \] x2 – 3x – 4 < 0.
Xét x2 – 3x – 4 = 0 \[ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 4\end{array} \right.\]
Ta có bảng xét dấu
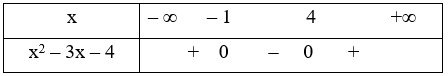
Dựa vào bảng xét dấu ta có x2 – 3x – 4 < 0 \[ \Leftrightarrow \] – 1 < x < 4
Kết hợp với điều kiện ta được: \[x \in \left( {\sqrt 5 ;4} \right)\]. Suy ra nghiệm nguyên dương của bất phương trình đã cho là: x = 3.
Vậy bất phương trình có 1 nghiệm nguyên dương.Câu 20:
Cho hàm số y = f(x) có đồ thị như hình sau:
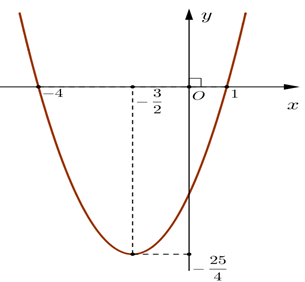
Hàm số đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đồ thị hàm số đi lên từ trái qua phải trên khoảng \[\left( {--\frac{{\rm{3}}}{{\rm{2}}}; + \infty } \right)\]nên hàm số đồng biến trên khoảng \[\left( {--\frac{3}{2}; + \infty } \right)\].
Câu 21:
Tìm tất cả các giá trị của a để bất phương trình ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\) \( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta = {\left( { - 1} \right)^2} - 4.a.a \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\1 - 4{a^2} \le 0\end{array} \right.\)
Xét tam thức bậc hai f(a) = 1 – a2, có ∆ = 02 – 4.(-4).1 = 16 > 0. Do đó f(a) có hai nghiệm phân biệt \(a = \frac{1}{2}\) và \(a = - \frac{1}{2}\)
Ta có bảng xét dấu
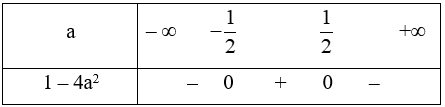
Dựa vào bảng xét dấu ta có 1 – 4a2 ≤ 0 \( \Leftrightarrow a \in \left( { - \infty ; - \frac{1}{2}} \right] \cup \left[ {\frac{1}{2}; + \infty } \right)\).
Kết hợp với điều kiện a > 0 suy ra a ∈ \(\left[ {\frac{1}{2}; + \infty } \right)\).
Vậy để ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\) thì a ∈ \(\left[ {\frac{1}{2}; + \infty } \right)\) hay a ≥ \(\frac{1}{2}\).
Câu 22:
Để f(x) = x2 + (m + 1)x +2m + 7 > 0 với mọi x thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có f(x) > 0 với \(\forall x \in \mathbb{R}\)\[\left\{ \begin{array}{l}a = 1 > 0\\\Delta = {(m + 1)^2} - 4.(2m + 7) < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\\Delta = {m^2} - 6m - 27 < 0\end{array} \right.\]
Xét tam thức bậc hai f(m) = m2 – 6m – 27, có ∆’ = 9 – (-27) = 36 > 0. Do đó f(m) có hai nghiệm phân biệt là m = -3 và m = 9.
Ta có bảng xét dấu

Dựa vào bảng xét dấu để ∆ < 0 thì – 3 < m < 9.
Vậy đáp án đúng là C.
Câu 23:
Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có f(x) > 0 vô nghiệm \( \Leftrightarrow f\left( x \right) \le 0\,\,\forall x \in \mathbb{R}\).
Xét m = 3 ta có f(x) = 5x – 4 với \(x > \frac{4}{5}\) thì f(x) > 0 nên m = 3 không thỏa mãn.
Xét m ≠ 3 ta có \(f\left( x \right) \le 0\,\,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a = m - 3 < 0\\\Delta = {m^2} + 20m - 44 \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < 3\\{m^2} + 20m - 44 \le 0\end{array} \right.\)
Xét tam thức bậc hai (biến m): m2 + 20m – 44 có ∆’ = 102 – (-44) = 144 > 0. Do đó tam thức có hai nghiệm phân biệt x = -22 và x = 2.
Ta có bảng xét dấu

Để \(f\left( x \right) \le 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}m < 3\\ - 22 \le m \le 2\end{array} \right. \Leftrightarrow - 22 \le m \le 2\)
Vậy đáp án đúng là B.
Câu 24:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
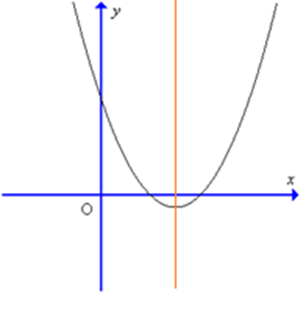
Kết luận nào sau đây đúng về hệ số a, b:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì bề lõm của đồ thị hướng lên trên nên a > 0;
Trục đối xứng của hàm số (đường màu đỏ) nằm bên phải trục Oy nên ta có trục đối xứng nhận giá trị dương hay \[{\rm{x}} = - \frac{{\rm{b}}}{{{\rm{2a}}}} > 0\] mà a > 0 nên b < 0.
Vậy a > 0 và b < 0.
Câu 25:
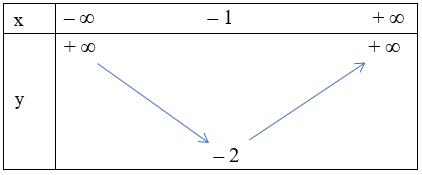
Hàm số y = x2 + 2x – 1 có bảng biến thiên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tọa độ đỉnh của hàm số là I(– 1; – 2)
Vì hệ số a > 0 nên hàm số đồng biến trên khoảng (– 1; + ∞) và nghịch biến trên khoảng (– ∞; – 1) ta có bảng biến thiên
Câu 26:
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Giao điểm của đồ thị với trục tung tại A(0; – 1) nên đồ hàm số cắt trục tung tại điểm có tung độ âm. Do đó chỉ có hình C và hình D thỏa mãn.
Hàm số có trục đối xứng \[x = \frac{3}{8} > 0\]nên trục đối xứng nằm về phần dương của trục Ox.
Do đó hình D là hình vẽ đúng.
Câu 27:
Tập xác định của hàm số \[y = \sqrt {x - 2} + \frac{{\sqrt {{x^2} - 1} }}{3}\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hàm số \[y = \sqrt {x - 2} + \frac{{\sqrt {{x^2} - 1} }}{3}\] xác định khi \[\left\{ \begin{array}{l}x - 2 \ge 0\\{x^2} - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x \le - 1\\x \ge 1\end{array} \right.\end{array} \right. \Leftrightarrow x \ge 2\].
Vậy tập xác định của hàm số là: D = [2; + ∞).
Câu 28:
Phương trình x2 – (m – 1)x + m2 – 3m + 2 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
x2 – (m – 1)x + m2 – 3m + 2 = 0 có 2 nghiệm trái dấu khi a.c < 0
⇔ 1. (m2 – 3m + 2) < 0
⇔ m2 – 3m + 2 < 0
⇔ 1 < m < 2
Vậy phương trình có 2 nghiệm trái dấu khi 1 < m < 2.
Đáp án đúng là D.
Câu 29:
Số giá trị nguyên của x thỏa mãn điều kiện xác định của phương trình :\(\sqrt {2 - x} + \frac{4}{{\sqrt {x + 1} + 3}} = 1\) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Điều kiện của phương trình : \(\left\{ \begin{array}{l}2 - x \ge 0\\x + 1 > 0\\\sqrt {x + 1} + 3 \ne 0\end{array} \right. \Leftrightarrow - 1 < x \le 2\).
Vì x ∈ ℤ nên x ∈ {0; 1; 2}.
Vậy có 3 giá trị nguyên của x thỏa mãn điều kiện xác định của phương trình đã cho.
Câu 30:
Phương trình \[(x + 4)(x + 1) - 3\sqrt {{x^2} + 5x + 2} = 6\] có bao nhiêu nghiệm nguyên âm:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Điều kiện của phương trình: x2 + 5x + 2 ≥ 0\[ \Leftrightarrow \left[ \begin{array}{l}x \ge \frac{{ - 5 + \sqrt {17} }}{2}\\x \le \frac{{ - 5 - \sqrt {17} }}{2}\end{array} \right.\]
\[(x + 4)(x + 1) - 3\sqrt {{x^2} + 5x + 2} = 6 \Leftrightarrow {x^2} + 5x + 4 - 3\sqrt {{x^2} + 5x + 2} = 6\]
Đặt \[\sqrt {{x^2} + 5x + 2} = t(t \ge 0)\]
\[{x^2} + 5x + 4 - 3\sqrt {{x^2} + 5x + 2} = 6 \Leftrightarrow {t^2} - 3t - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 1\\t = 4\end{array} \right.\]
Kết hợp với điều kiện t = 4 thỏa mãn
Với t = 4 ta có \[\sqrt {{x^2} + 5x + 2} = 4 \Leftrightarrow {x^2} + 5x - 14 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 7\end{array} \right.\]
Vậy phương trình đã cho có 1 nghiệm nguyên âm.
