Trắc nghiệm Toán 10 Bài 6. Tích vô hướng của hai vectơ có đáp án
Trắc nghiệm Toán 10 Bài 6. Tích vô hướng của hai vectơ có đáp án
-
510 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho và là hai vectơ cùng hướng và đều khác vectơ . Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: .
Do và là hai vectơ cùng hướng nên .
Vậy .
Câu 2:
Cho và khác vectơ . Xác định góc giữa hai vectơ và khi
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: .
Mà theo giả thiết , suy ra
Câu 3:
Cho hai vectơ và thỏa mãn và Xác định góc giữa hai vectơ và
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có:Câu 4:
Cho hai vectơ và thỏa mãn và hai vectơ và vuông góc với nhau. Xác định góc giữa hai vectơ và .
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
Suy ra
Câu 5:
Cho hai vectơ và . Đẳng thức nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Nhận thấy C và D chỉ khác nhau về hệ số và nên đáp án sai rơi vào C hoặc D.
Ta có:
- A đúng, vì:
B đúng, vì
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xác định được góc là góc nên (do tam giác ABC đều)
Do đó
Câu 7:
Cho tam giác đều ABC có cạnh bằng a Tính tích vô hướng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xác định được góc là góc ngoài của góc nên (do tam giác ABC là tam giác đều nên góc , do đó, góc ngoài của góc B có số đo là 120o).
Do đó
Câu 8:
Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
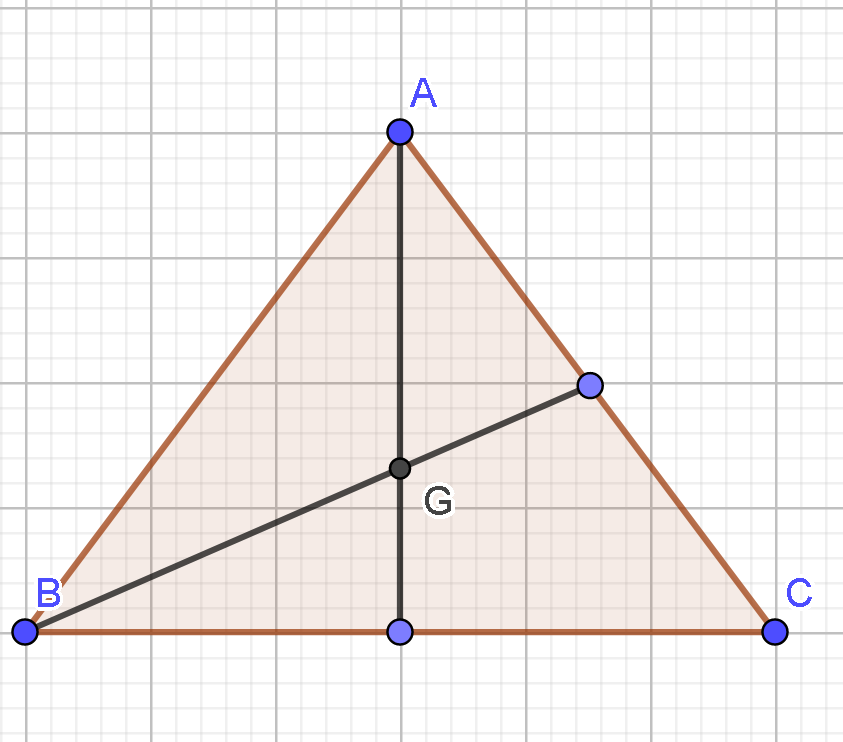
- Xác định được góc là góc nên (do tam giác ABC đều)
Do đó A đúng
- Xác định được góc là góc ngoài của góc nên
Do đó B đúng.
Xác định được góc là góc nên
Ta có: AG nằm trên đường trung tuyến cũng chính là đường cao của tam giác đều ABC, ta tính được đường cao, suy ra: AG = .a.= .
Tương tự, GB = .
Do đó C sai.
Xác định được góc là góc nên
Do đó D đúng.
Câu 9:
Cho tam giác đều ABC có cạnh bằng a và chiều cao AH. Mệnh đề nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
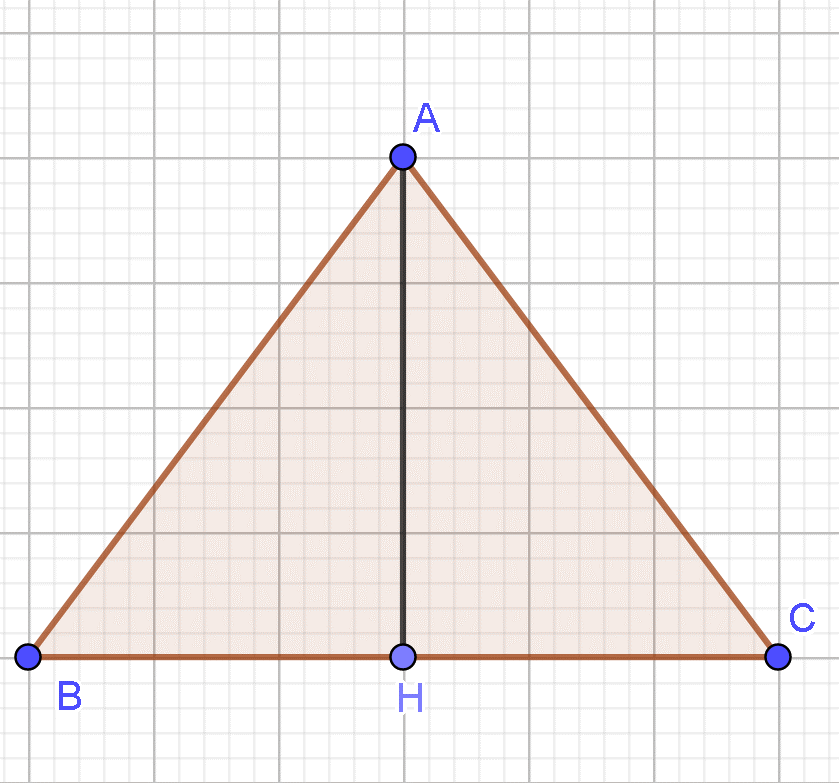
Xác định được góc là góc ngoài của góc nên (vì tam giác ABC đều nên góc A = 60o, do đó góc ngoài của góc A bằng 120o).
Do đó
+) A đúng vì nên suy ra
+) B đúng vì AH chính là tia phân giác nên
+) C đúng vì
Câu 10:
Cho tam giác ABC vuông cân tại A và có Tính
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
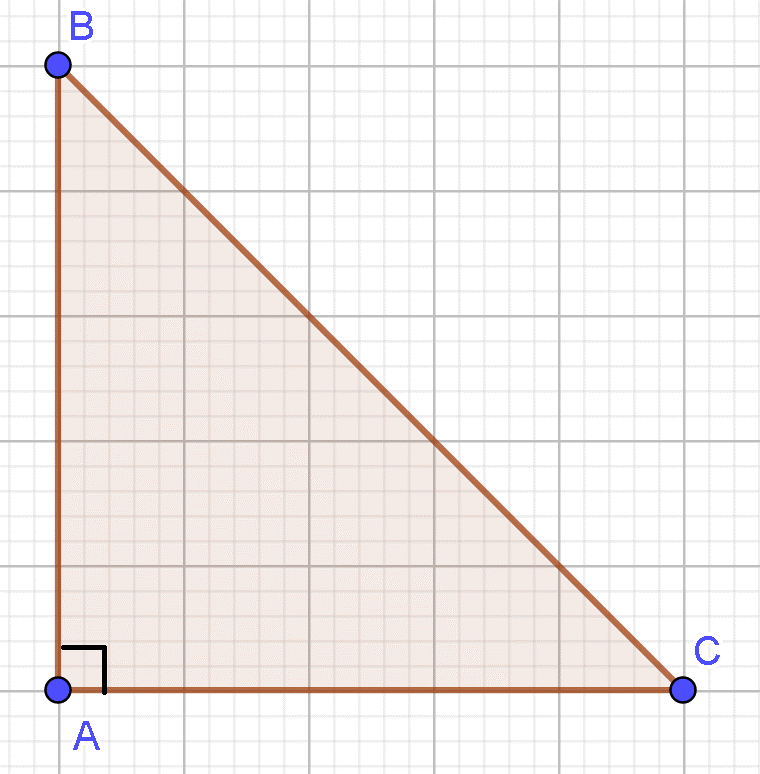
Xác định được góc là góc ngoài của góc ![]() nên (Tam giác ABC vuông cân tại A, suy ra góc )
nên (Tam giác ABC vuông cân tại A, suy ra góc )
Độ dài BC là:
Do đó
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
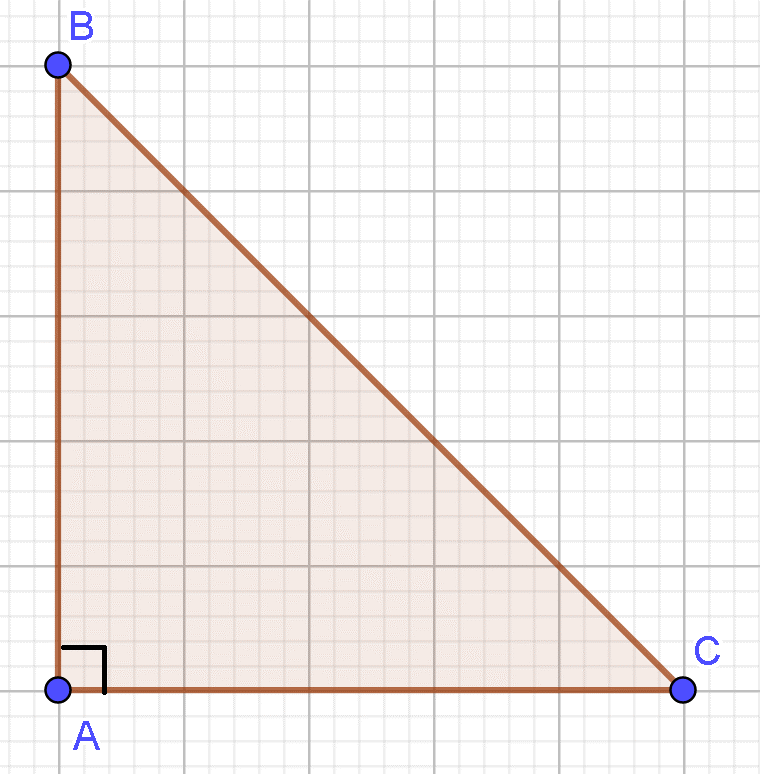
Do tam giác ABC vuông cân tại A nên suy ra = 0
Câu 12:
Cho tam giác ABC vuông tại A và có AB = c; AC = b. Tính
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
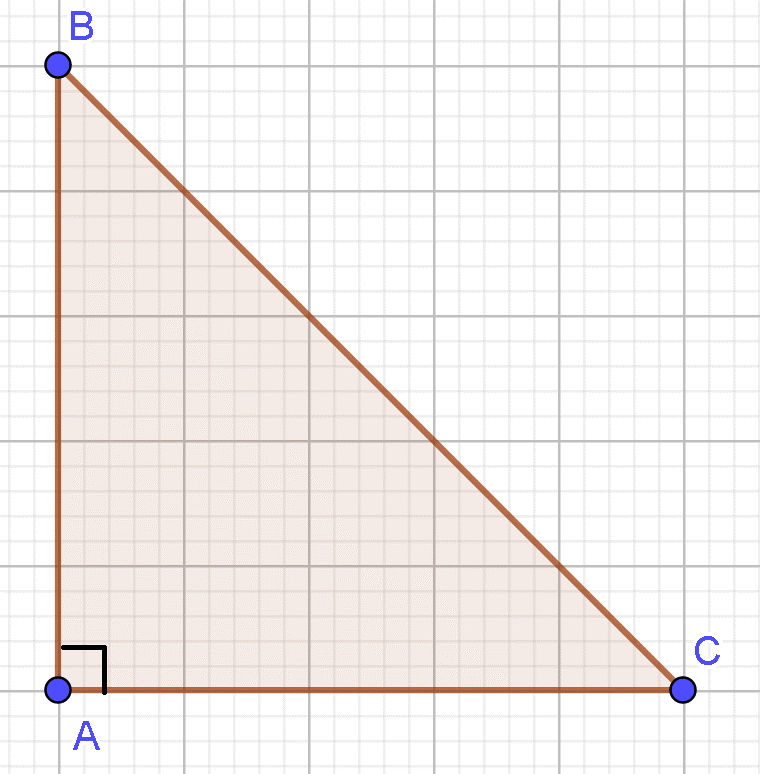
Áp dung định lý Py – ta – go ta có:
Cos B =
Lại có: cos B chính là cos
Ta có:
Câu 14:
Cho tam giác ABC có Gọi M là trung điểm cạnh BC Tính
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì M là trung điểm của BC suy ra
Khi đó
Câu 15:
Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
Do đó, tam giác OAB cân tại O.
