15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 3. Các phép toán trên tập hợp có đáp án

Câu 1:

Điền vào chỗ trống: “Tập hợp các phần tử thuộc A hoặc thuộc B gọi là ….”

A. hợp của hai tập hợp;

B. giao của hai tập hợp;

C. hai tập hợp bằng nhau;

D. phần bù của hai tập hợp.

Xem đáp án

Đáp án đúng là: A

Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp, kí hiệu A ∪ B.

Câu 2:

Giao của hai tập hợp A và B kí hiệu như thế nào?

A. A ∪ B;

B. A = B;

C. A ∩ B;

D. A ⊆ B.

Xem đáp án

Đáp án đúng là: C

Giao của hai tập hợp A và B kí hiệu là A ∩ B.

Câu 3:

Điền vào chỗ trống: “Hiệu của tập hợp A và tập hợp B là ….”

A. tập hợp các phần tử thuộc B nhưng không thuộc A;

B. tập hợp các phần tử thuộc A nhưng không thuộc B;

C. tập hợp các phần tử thuộc B và thuộc A;

D. tập hợp các phần tử thuộc B hoặc thuộc A.

Xem đáp án

Đáp án đúng là: B

Hiệu của tập hợp A và tập hợp B là tập hợp các phần tử thuộc A nhưng không thuộc B, kí hiệu là A\B

Câu 4:

Kí hiệu C_UA có nghĩa là gì?

A. A là tập con của U;

B. U là tập con của A;

C. Tập A bằng tập U;

D. Phần bù của A trong U.

Xem đáp án

Đáp án đúng là: D

Nếu A là tập con của U thì hiệu U\A gọi là phần bù của A trong U và kí hiệu C_UA.

Câu 5:

Nếu A và B là tập hợp hữu hạn thì công thức nào sau đây đúng?

A. n(A ∪ B) = n(A) + n(B);

B. n(A ∪ B) = n(A) + n(B) – n(A ∩ B);

C. n(A ∪ B) = n(A) - n(B);

D. n(A ∪ B) = n(A) + n(B) + n(A ∩ B).

Xem đáp án

Đáp án đúng là: B

Nếu A và B là tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) – n(A ∩ B).

Câu 6:

Nếu A và B không có phần tử chung thì:

A. n(A ∪ B) = n(A) ‒ n(B);

B. n(A ∪ B) = n(A ∩ B);

C. n(A ∪ B) = n(A) × n(B);

D. A ∩ B = ∅.

Xem đáp án

Đáp án đúng là: D

Nếu A và B không có phần tử chung thì A ∩ B = ∅.

Câu 7:

Xác định M = A ∩ B trong trường hợp A là tập hợp các tam giác đều, B là tập hợp các tam giác cân?

A. M là tập hợp các tam giác cân;

B. M là tập hợp các tam giác đều;

C. M là tập hợp các đa giác;

D. M là tập hợp các tam giác.

Xem đáp án

Đáp án đúng là: B

Nếu một tam giác là tam giác đều thì chắc chắn sẽ là tam giác cân, do đó A là tập con của B nên A ∩ B = A = M.

Vậy M là tập hợp các tam giác đều.

Câu 8:

Xác định M = A ∪ B trong trường hợp A = {x | x ∈ ℕ, x ⋮ 4 và x < 10}, B là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 12.

A. M = {0; 3; 4; 6; 8; 9};

B. M = {0; 4; 6; 8; 9};

C. M = {0; 3; 4; 6; 8; 9; 12};

D. M = {0; 3; 6; 8; 9}.

Xem đáp án

Đáp án đúng là: A

Liệt kê các phần tử ta có: A = {0; 4; 8} và B = {0; 3; 6; 9}.

Vậy M = A ∪ B = {0; 3; 4; 6; 8; 9}.

Câu 9:

Lớp 10A có 22 bạn chơi bóng đá, 25 bạn chơi cầu lông và 15 bạn chơi cả hai môn thể thao này. Hỏi lớp 10A có bao nhiêu bạn chơi ít nhất một trong hai môn?

A. 47;

B. 32;

C. 7;

D. 3.

Xem đáp án

Đáp án đúng là: B

Gọi A là tập hợp các học sinh của lớp 10A chơi bóng đá và B là tập hợp các học sinh của lớp 10A chơi cầu lông.

Số phần tử của A và B lần lượt là n(A) và n(B) nên n(A) = 22; n(B) = 25.

Ta có:

+) Tập hợp số học sinh chơi cả hai môn thể thao bóng đá và cầu lông là A ∩ B nên n(A ∩ B) =15.

+) Tập hợp số học sinh chơi ít nhất 1 trong 2 môn thể thao đó là A ∪ B.

Nên tổng số học sinh chơi ít nhất 1 trong 2 môn thể thao là n(A ∪ B).

Suy ra n(A ∪ B) = n(A) + n(B) ‒ n(A ∩ B) = 22 + 25 – 15 = 32.

Vậy có 32 học sinh chơi ít nhất một trong hai môn thể thao bóng đá và cầu lông.

Câu 10:

Lớp 10E của trường có 30 học sinh thích môn Vật lí, 15 học sinh thích môn Hóa học và 10 học sinh thích cả môn Vật lí và Hóa học. Hỏi lớp 10A có bao nhiêu học sinh chỉ thích Vật lí hoặc chỉ thích Hóa học biết mỗi học sinh của lớp đều thích môn Vật lí hoặc Hoá học.

A. 10;

B. 15;

C. 25;

D. 30.

Xem đáp án

Đáp án đúng là: C

Gọi A là tập hợp số học sinh thích môn Vật lí.

B là tập hợp số học sinh thích môn Hóa học.

Số phần tử của A và B lần lượt là n(A) và n(B) thì n (A) = 30, n(B) = 15.

Ta có:

+) Tập hợp số học sinh thích cả hai môn Vật lí và Hoá học là: A ∩ B nên n(A ∩ B) = 10.

+) Tập hợp số học sinh thích ít nhất 1 trong 2 môn Vật lí và môn Hóa học là A ∪ B.

Nên số học sinh thích ít nhất một trong hai môn đó là n(A ∪ B).

Suy ra n(A ∪ B) = n(A) + n(B) - n(A ∩ B) = 30 + 15 – 10 = 35.

Vậy số học sinh chỉ thích môn Vật lí hoặc chỉ thích môn Hóa học là:

n(A ∪ B) - n(A ∩ B) = 35 – 10 = 25.

Câu 11:

Dùng kí hiệu đoạn, khoảng, nửa khoảng viết tập hợp sau:

A. (1; 4);

B. (‒1; 4];

C. [‒1; 4];

D. [1; 4].

Xem đáp án

Đáp án đúng là: C

Cách 1:

Ta thấy trên trục số biểu diễn [‒1; 4].

Cách 2:

Phương án A: (1; 4)

Phương án B: (‒1; 4]

Phương án C: [‒1; 4]

Phương án D: [1; 4]

Kí hiệu [‒1; 4] là đúng.

Câu 12:

Xác định tập hợp sau đây trên trục số: C = (7; 12] ∩ (‒∞; 9]:

A.

B.

C.

D. Không xác định.

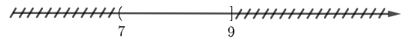
Xem đáp án

Đáp án đúng là: C

Để xác định tập C, ta vẽ sơ đồ sau đây:

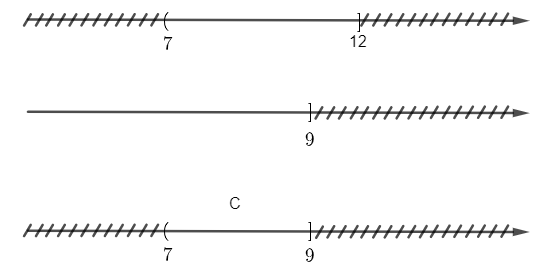
Từ sơ đồ ta thấy, C = (7; 9].

Câu 13:

Xác định tập hợp M = (A ∪ B) ∩ C trong trường hợp:

A là tập hợp các hình vuông, B là tập hợp các hình thoi, C là tập hợp các hình chữ nhật.

A. M là tập hợp các hình chữ nhật;

B. M là tập hợp các hình thoi;

C. M là tập hợp các hình vuông;

D. M là tập hợp các tứ giác;

Xem đáp án

Đáp án đúng là: C

Nếu một hình là hình vuông thì hình đó luôn luôn là hình thoi nên A ⊂ B.

Khi đó A ∪ B = B suy ra M = (A ∪ B) ∩ C = B ∩ C.

Hình vuông vừa là hình chữ nhật đặc biệt và sẽ vừa là hình thoi đặc biệt.

Vậy M = B ∩ C là tập hợp các hình vuông.

Câu 14:

Xác định A ∩ B trong trường hợp sau:

A = {(x; y)| x, y ∈ ℝ, 3x – y = 7}, B = {(x; y)| x, y ∈ ℝ, x – y = 1},

A. {(3; 2)};

B. {3}, {2};

C. {3; 2};

D. ∅.

Xem đáp án

Đáp án đúng là: A

Tập hợp A ∩ B là tập hợp cặp số (x; y) thỏa mãn hệ phương trình:

Vậy A ∩ B = {(3; 2)}.

Câu 15:

Vùng tô đậm thể hiện mối quan hệ gì giữa 2 tập hợp A, B:

A. A ∩ B;

B. A ∪ B;

C. A\B;

D. C_BA.

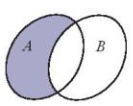
Xem đáp án

Đáp án đúng là: C

Phần bôi đậm thể hiện phần tử thuộc A nhưng không thuộc B, vậy vùng tô đậm là hiệu của A và B, kí hiệu là A\B.

Trắc nghiệm Toán 10 Bài 3. Các phép toán trên tập hợp có đáp án

Trắc nghiệm Toán 10 Bài 3. Các phép toán trên tập hợp có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương