Trắc nghiệm Toán 10 Bài 2. Hàm số bậc hai có đáp án
Trắc nghiệm Toán 10 Bài 2. Hàm số bậc hai có đáp án
-
225 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trong các hàm số sau, hàm số nào là hàm số bậc hai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Hàm số bậc hai ẩn x là hàm số cho bởi công thức có dạng y = f(x) = ax2 + bx + c với a, b, c là các số thực và a khác 0. Ta thấy chỉ có câu B là hàm số có dạng y = f(x) = ax2 + bx + c với a = 1 ≠ 0; b = 2, c = - 1.
Vậy ta chọn phương án B.
Câu 2:
Điền vào chỗ trống: Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) là một ….
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) là một Parabol.
Câu 3:
Bề lõm của parabol quay lên trên đối với đồ thị hàm số bậc hai nào sau đây?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Bề lõm của parabol quay lên trên khi hàm số bậc hai có giá trị a > 0.
Trong các đáp án A, B, C, D ta thấy chỉ có câu C là a = 1 > 0, các câu A, B, D đều có hệ số a < 0 nên câu C đúng.
Câu 4:
Một chiếc cổng hình parabol có dạng đồ thị giống đồ thị hàm số y =- x2 như hình vẽ. Cổng có chiều rộng d = 8 m. Tính chiều cao h của cổng.
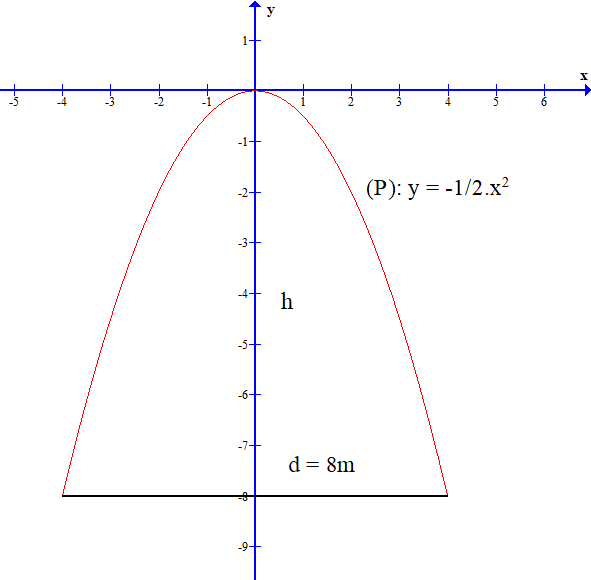
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Gọi A là 1 điểm nằm ở bên phải chân cổng.
Hoành độ điểm A là bằng một nửa chiều rộng của cổng.
Tung độ của điểm A bằng chiều cao của cổng.
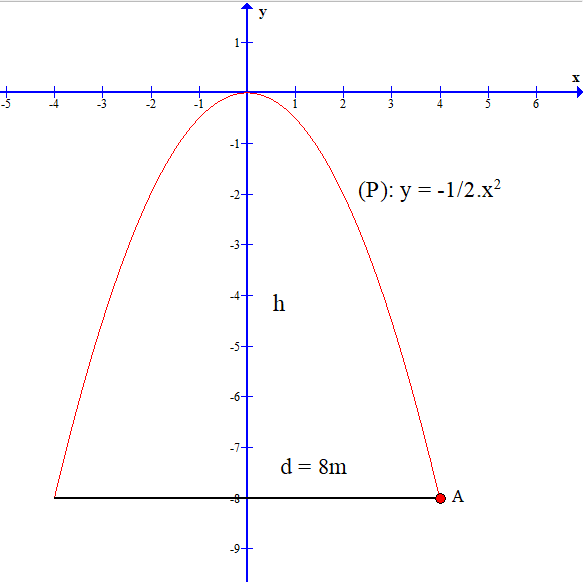
Parabol (P): y = x2 có d = 8 m, suy ra .
A thuộc (P) suy ra yA = . 42 = ‒8.
Vậy chiều cao của cổng là h = 8 m.
Câu 5:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = 2x2 + 4x + 3 có trục đối xứng là đường thẳng nào?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Hàm số bậc hai y = 2x2 + 4x + 3 xác định các tham số: a = 2; b = 4; c = 3.
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax2 + bx + c có trục đối xứng là đường thẳng x = .
Vậy đồ thị bậc hai y = 2x2 + 4x + 3 có trục đối xứng là đường thẳng x = - 1.
Câu 6:
Tìm tọa độ đỉnh S của parabol: y = x2 – 2x + 1?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) là một parabol (P): Có đỉnh S với hoành độ , tung độ ; (Δ = b2 – 4ac)
Với hàm số y = x2 – 2x + 1 có a = 1, b = - 2, c = 1 thì đỉnh S có toạ độ là:
= 1, = 0.
Vậy S(1; 0).
Câu 7:
Điểm nào sau đây thuộc đồ thị hàm số bậc hai y = 2x2 – 3x + 1?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Câu A: Thay x = 1; y = 0 vào hàm số đã cho ta có: 0 = 2. 12 – 3. 1 + 1 = 0 là mệnh đề đúng. Vậy M(1; 0) thuộc đồ thị hàm số đã cho.
Câu B: Thay x = 2; y = 1 vào hàm số đã cho ta có: 1 = 2. 22 – 3. 2 + 1 = 3 là mệnh đề sai. Vậy N(2; 1) không thuộc đồ thị hàm số đã cho.
Câu C: Thay x = 3; y = 2 vào hàm số đã cho ta có: 2 = 2. 32 – 3. 3 + 1 = 10 là mệnh đề sai. Vậy P(3; 2) không thuộc đồ thị hàm số đã cho.
Câu D: Thay x = 4; y = 3 vào hàm số đã cho ta có: 3 = 2. 42 – 3. 4 + 1 = 21 là mệnh đề sai. Vậy Q(4; 3) không thuộc đồ thị hàm số đã cho.
Vậy ta chọn phương án A.
Câu 8:
Hàm số y = 2x2 – 4x + 1 đồng biến và nghịch biến trên khoảng nào?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) trong trường hợp a > 0 thì hàm số nghịch biến trên khoảng và đồng biến trên khoảng ; trong trường hợp a < 0 thì hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
Với hàm số y = 2x2 – 4x + 1 có a = 2 > 0, b = ‒4 nên hàm số nghịch biến trên khoảng (‒∞; 1) và đồng biến trên khoảng (1; +∞).
Câu 9:
Cho hàm số y = x2 – 3x + 2. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Câu A: Hàm số bậc hai y = x2 – 3x + 2 có tập xác định là ℝ. Khẳng định A sai.
Câu B: Xét điểm M(1; 0): thay x = 1; y = 0 vào hàm số ta có: 0 = 12 – 3. 1 + 2 = 0 là mệnh đề đúng. Vậy M(1; 0) thuộc đồ thị hàm số. Khẳng định B đúng.
Câu C: Hàm số y = x2 – 3x + 2 có a = 1 > 0, b = ‒3 nên hàm số nghịch biến trên khoảng và đồng biến trên khoảng . Khẳng định C sai.
Câu D: Hàm số y = x2 – 3x + 2 có a = 1 > 0 nên đồ thị hàm số có bề lõm quay lên trên. Khẳng định D sai.
Vậy ta chọn phương án B.
Câu 10:
Tìm m để hàm số y = 2(m – 1)x2 + x – 2 là hàm số bậc hai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Hàm số y = 2(m – 1)x2 + x – 2 là hàm số bậc hai khi hệ số của x2 khác 0
⇔ 2(m – 1) ≠ 0 ⇔ m ≠ 1.
Vậy m ∈ ℝ\{1}.
Câu 11:
Cho hàm số y = x2 + 2x + 4. Hàm số đạt giá trị nhỏ nhất là bao nhiêu?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Hàm số bậc hai y = ax2 + bx + c (với a ≠ 0), khi a > 0, hàm số đạt giá trị nhỏ nhất bằng tại x = .
Ta thấy hàm số y = x2 + 2x + 4 có a = 1 > 0, b = 2, c = 4
Và ∆ = b2 – 4ac = 22 – 4.1.4 = ‒12
Do đó hàm số có giá trị nhỏ nhất bằng = 3 tại x = = 1.
Vậy hàm số đạt giá trị nhỏ nhất là 3 khi x = 1.
Câu 12:
Cho một vật rơi từ trên cao xuống theo phương thẳng đứng với vận tốc ban đầu là 12 m/s. Hỏi lúc t = 7 s thì vật đã rơi được bao nhiêu mét, biết g = 9,8 m/s2, hệ trục tọa độ chọn mốc từ lúc vật bắt đầu rơi, gốc tọa độ ở vật tại thời điểm bắt đầu rơi.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Gọi vận tốc ban đầu của vật là v0 = 12 m/s.
Do đây là vật rơi nên vật sẽ chuyển động nhanh dần đều.
Suy ra hàm số biểu thị quãng đường rơi s theo thời gian t là:
s = v0t + gt2.
Ta thấy hệ trục tọa độ chọn mốc từ lúc vật bắt đầu rơi, gốc tọa độ ở vật tại thời điểm bắt đầu rơi và thời gian là đại lượng không âm nên t ≥ 0.
Ta có hàm số: s = f(t) = 12t + = 12t + 4,9t2.
Khi t = 7 thì vật đã rơi được quãng đường là:
s = f(7) = 12.7 + 4,9. 72 = 324,1 (m).
Vậy ta chọn phương án A.
Câu 13:
Tìm m để đồ thị hàm số y = mx2 + 2(m – 1)x + 1 có trục đối xứng là x = ‒1?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Đồ thị hàm số y = mx2 + 2(m – 1)x + 1 có trục đối xứng là x = ‒1
⇔ hàm số đã cho là hàm số bậc hai và có = ‒1
⇔ ⇔ ⇔ (vô lí)
Vậy không có giá trị của m thỏa mãn.
Câu 14:
Hàm số nào sau đây có đỉnh S(1; 0):
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) là một parabol (P) có đỉnh S với hoành độ , tung độ ; (Δ = b2 – 4ac)
Câu A: Hàm số y = 2x2 + 1 có các hệ số a = 2, b = 0, c = 1 nên có tọa độ đỉnh S(0; 1).
Câu B: Hàm số y = x2 – 2x + 1 có các hệ số a = 1, b = ‒2, c = 1 nên có tọa độ đỉnh S(1; 0).
Câu C: Hàm số y = x2 có các hệ số a = 1; b = 0, c = 0 nên có tọa độ đỉnh S(0; 0).
Câu D: Hàm số y = 2x2 ‒ 1 có các hệ số a = 2; b = 0, c = ‒1 nên có tọa độ đỉnh S(0; ‒1).
Vậy ta chọn phương án B.
Câu 15:
Hình nào sau đây là đồ thị của hàm số ?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Cách 1:
Vẽ đồ thị hàm số (a = ; b = 1, c = 0):
Trong mặt phẳng toạ độ Oxy, đồ thị hàm số bậc hai là một parabol (P):
+ Có toạ độ đỉnh S với tung độ hay
+ Có trục đối xứng là đường thẳng x = (đường thẳng này song song với trục Oy và đi qua đỉnh S);
+ Bề lõm của parabol (P) quay xuống dưới do < 0;
+ Đồ thị hàm số cắt trục tung tại điểm O(0; 0) và cắt trục hoành tại điểm A(2; 0).
Ta có đồ thị hàm số:
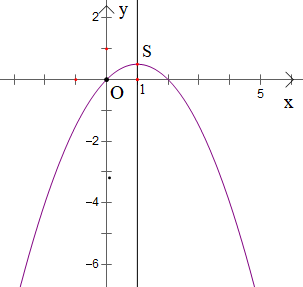
Vậy đáp án D đúng.
Cách 2:
Hàm số có các hệ số a = < 0, b = 1, c = 0
- Vì a = < 0 nên đồ thị hàm số có bề lõm quay xuống dưới, ta loại B và C.
- Đồ thị có toạ độ đỉnh S với tung độ hay Do đó ta loại A.
Vậy ta chọn D.
