Trắc nghiệm Toán 10 CTST Bài 1. Hàm số và đồ thị có đáp án (Nhận biết)
-
228 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho bảng dữ liệu sau về số sản phẩm bán được trong 7 ngày của một cửa hàng thời trang:
|
Ngày |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Số sản phẩm |
25 |
35 |
40 |
30 |
37 |
50 |
60 |
Bảng dữ liệu trên có biểu thị cho ta một hàm số không? Nếu có hãy xác định tập xác định của hàm số đó.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Từ bảng dữ liệu đã cho, ta thấy ứng với mỗi thời điểm (ngày) trong bảng đều có một giá trị số lượng sản phẩm bán được duy nhất.
Vì vậy bảng trên biểu thị một hàm số.
Hàm số đó có tập xác định D = {1; 2; 3; 4; 5; 6; 7}.
Vậy ta chọn phương án D.
Câu 2:
Cho bảng dữ liệu sau thống kê về doanh thu mỗi tháng (đơn vị: triệu đồng) của một cửa hàng trong 6 tháng cuối năm 2021:
|
Tháng |
7 |
8 |
9 |
10 |
11 |
12 |
|
Doanh thu |
30 |
35 |
28 |
40 |
50 |
70 |
Tập xác định D và tập giá trị T của hàm số cho bằng bảng trên là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta thấy ứng với mỗi thời điểm (tháng) trong bảng, ta đều có một giá trị doanh thu duy nhất.
Vì vậy biến số x là tháng và y là doanh thu.
Do đó ta có:
+) D = {7; 8; 9; 10; 11; 12};
+) T = {30; 35; 28; 40; 50; 70}.
Vậy ta chọn phương án B.
Câu 3:
Cho biểu đồ sau đây thể hiện tốc độ tăng của nhóm hàng điện tử, máy tính và linh kiện (đơn vị: %) của Việt Nam trong giai đoạn 2015 – 2020 (Theo số liệu của Tổng cục Thống kê):
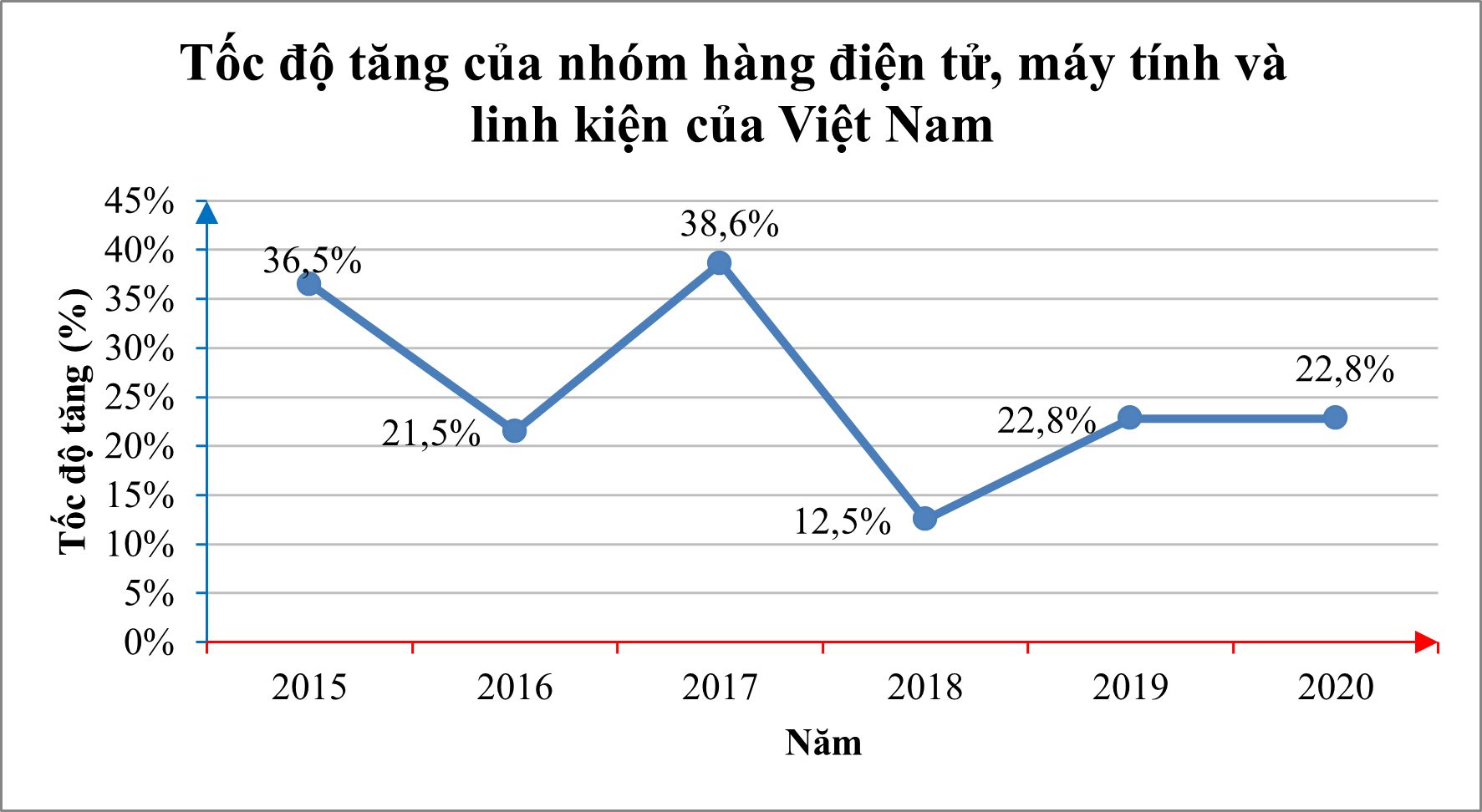
Tập giá trị của hàm số cho bằng biểu đồ trên là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta thấy ứng với mỗi thời điểm (năm) trong biểu đồ, ta đều có một giá trị tốc độ tăng duy nhất.
Vì vậy biến số x là năm và y là tốc độ tăng.
Do đó ta có tập giá trị T = {36,5%; 21,5%; 38,6%; 12,5%; 22,8%; 22,8%}.
Phương án A sai vì không có giá trị 22,8%.
Vậy ta chọn phương án C.
Câu 4:
Biểu đồ sau đây cho biết tình hình xuất siêu (xuất khẩu trừ nhập khẩu) của nước ta giai đoạn 2017 – Sơ bộ 2021 (Theo số liệu của Tổng cục Thống kê):
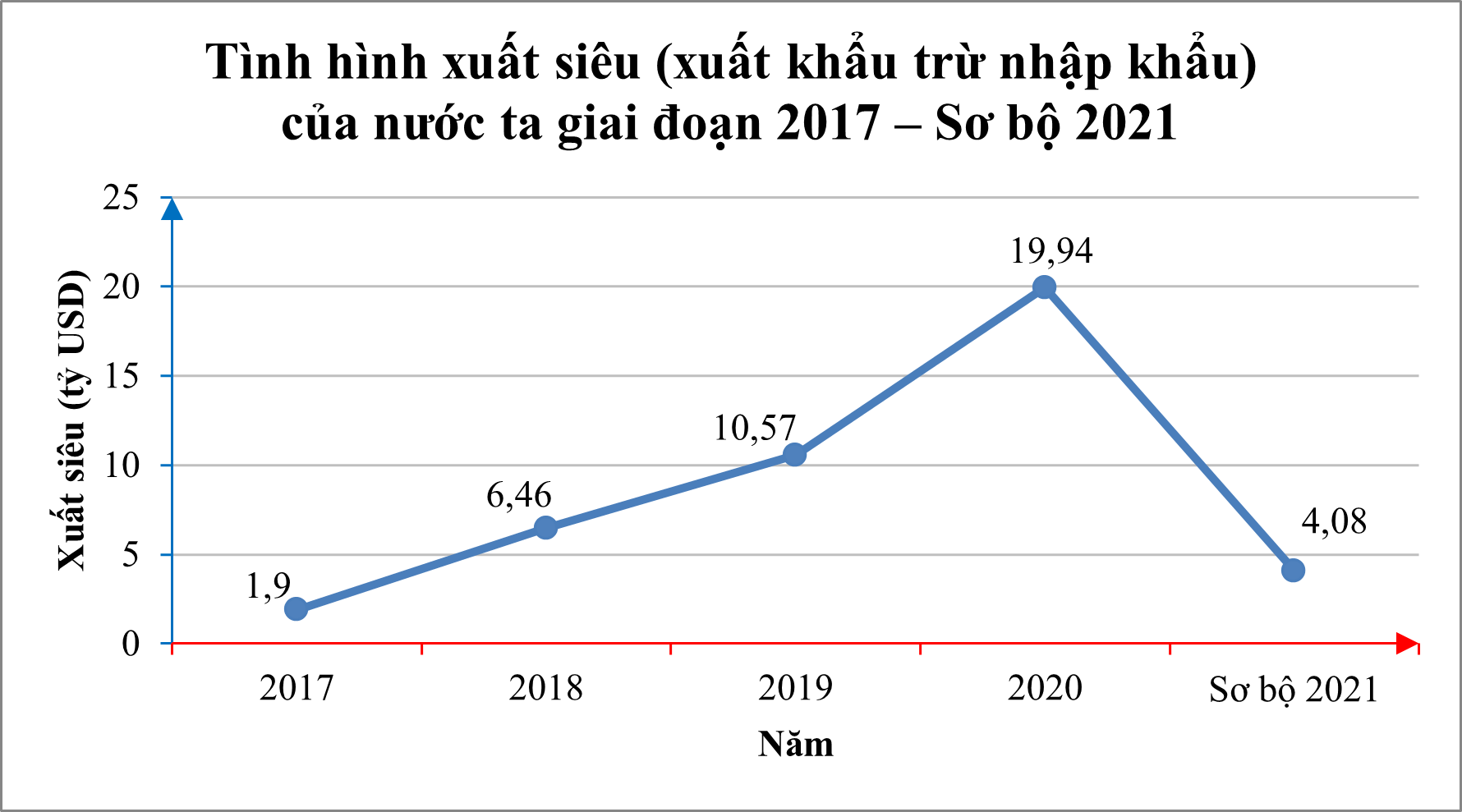
Biểu đồ trên có biểu thị cho ta một hàm số không? Nếu có hãy xác định tập giá trị của hàm số đó.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Từ biểu đồ đã cho, ta thấy ứng với mỗi thời điểm (năm) trong biểu đồ đều có một giá trị xuất siêu duy nhất.
Vì vậy biểu đồ trên biểu thị một hàm số.
Hàm số đó có giá trị T = {1,9; 6,46; 10,57; 19,94; 4,08}.
Vậy ta chọn phương án A.
Câu 5:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Hàm số y = f(x) đồng biến trên K nếu ∀x1, x2 ∈ K, x1 < x2 Þ f(x1) < f(x2).
Hàm số y = f(x) nghịch biến trên K nếu ∀x1, x2 ∈ K, x1 < x2 Þ f(x1) > f(x2).
Vậy ta chọn phương án D.
Câu 6:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Khi hàm số nghịch biến (giảm) trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.
Do đó ta chọn phương án B.
Câu 7:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta đặt \(y = f\left( x \right) = - \frac{x}{2} + 2\).
• Với x = 0, ta có f(0) = \( - \frac{0}{2} + 2 = 2\).
Khi đó đồ thị hàm số đã cho đi qua điểm M(0; 2).
Do đó ta loại phương án C và D.
• Với y = 0, ta có f(x) = \( - \frac{x}{2} + 2 = 0\)
Þ \( - \frac{x}{2} = - 2\) Þ x = 4.
Khi đó đồ thị hàm số đã cho đi qua điểm N(4; 0).
Do đó ta loại phương án B.
Vì vậy đồ thị ở phương án A là đồ thị của hàm số đã cho.
Vậy ta chọn phương án A.