Trắc nghiệm Phân tích một số ra thừa số nguyên tố có đáp án ( Vận dụng )
Trắc nghiệm Phân tích một số ra thừa số nguyên tố có đáp án ( Vận dụng )
-
49 lượt thi
-
5 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Các ước của 24là: 1; 2; 22= 4; 23= 8; 2 4= 16
Vậy các ước của 24là 1, 2, 4, 8, 16.
Do đó ta viết tập hợp A: A = {1; 2; 4; 8; 16}.
Chọn đáp án D.
Câu 2:
Cho số 150 = 2 . 3 . 52, số lượng ước của 150 là bao nhiêu?
Xem đáp án
Lý thuyết: Nếu m = ax. by. cz, với a, b, c là số nguyên tố thì m có (x + 1)(y + 1)(z + 1) ước.
Phân tích số 150 ra thừa số nguyên tố:
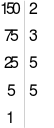
Ta có: 150 = 2 . 3 . 52với x = 1; y = 1; z = 2
Vậy số lượng ước số của 150 là (1 + 1)(1 + 1)(2 + 1) = 12 ước.
Chọn đáp án D.
Câu 3:
Cho a = 22. 7, hãy viết tập hợp Ư(a) tất cả các ước của a.
Xem đáp án
Ta có: a = 22. 7 = 4 . 7 = 28
28 = 28 . 1 = 14 . 2 = 7 . 4 = 7 . 2 . 2
Do đó ta tìm được các ước của 28 là: 1, 2, 4, 7, 14, 28.
Vậy Ư(28) = {1; 2; 4; 7; 14; 28}.
Chọn đáp án D.
Câu 4:
Xem đáp án
Lý thuyết: Nếu m = ax. by. cz, với a, b, c là số nguyên tố thì m có (x + 1)(y + 1)(z + 1) ước.
Vậy ta phân tích các số đã cho ra thừa số nguyên tố rồi tìm các ước của số đó.
1 464 = 23. 3 . 61 có (3 + 1)(1 + 1)(1 + 1) = 16 ước
496 = 24. 31 có (4 + 1)(1 + 1) = 10 ước
1 035 = 32. 5 . 23 có (2 + 1)(1 + 1)(1 + 1) = 12 ước
1 517 = 37 . 41 có (1 + 1)(1 + 1) = 4 ước
Vậy số tự nhiên có ước nhiều nhất là 1 464.
Chọn đáp án A.
Câu 5:
Xem đáp án
Ta tính tổng: 1 + 2 + 3 + … + n
Ta thấy tổng trên có: (n – 1) : 1 + 1 = n (số hạng)
Do đó: 1 + 2 + 3 + … + n = n . (n + 1) : 2
Theo đề bài ta được: n . (n + 1) : 2 = 465
Suy ra: n . (n + 1) = 465 . 2 = 930
Nhận thấy tích n . (n + 1) là tích của hai số tự nhiên liên tiếp.
Do đó ta phân tích 930 ra thừa số nguyên tố sau đó phân tích thành tích, ta được:
930 = 2 . 3 . 5 . 31 = (2 . 3 . 5) . 31 = 30 . 31 = 30 . (30 + 1)
Khi đó: n . (n + 1) = 30 . (30 + 1)
Vậy n = 30.
Chọn đáp án D.