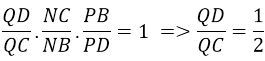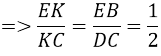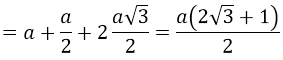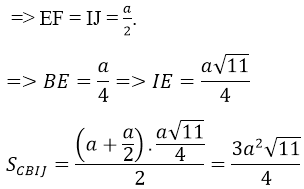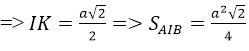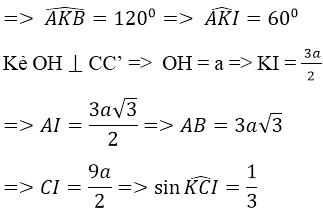Trắc nghiệm Ôn tập cuối năm Hình học 11 có đáp án
Trắc nghiệm Ôn tập cuối năm Hình học 11 có đáp án
-
98 lượt thi
-
30 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Câu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Có thể sửa lại các câu sai thành các câu đúng như sau:
A. Qua hai đường thẳng bất kì không xác định một mặt phẳng duy nhất
B. Qua một đường thẳng và một điểm nằm ngoài nó xác định một mặt phẳng duy nhất.
C. Qua hai đường thẳng cắt nhau xác định một mặt phẳng duy nhất
D. Qua hai đường thẳng không có điểm chung chưa kết luận được chúng xác định mặt phẳng duy nhất
Đáp án C
Câu 2:
Câu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Có thể sửa lại các câu sau thành các câu đúng như sau:
A. Nếu ba điểm cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng
B. Hai mặt phẳng phân biệt có một điểm chung thì chúng cắt nhau theo giao tuyến đi qua điểm chung ấy
C. Nếu hai đường thẳng không có điểm chung thì chưa kết luận được chúng không cùng nằm trong một mặt phẳng
D. Nếu hai đường thẳng có một điểm chung thì chúng cùng nằm trong một mặt phẳng
Đáp án D
Câu 3:
Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì:
 Xem đáp án
Xem đáp án
Đáp án A
Câu 5:
Câu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Có thể sủa lại các câu sai thành các câu đúng như sau:
A. Hai đường thẳng cùng nằm trên một mặt phẳng và không có điểm chung thì song song với nhau
B. Hai mặt phẳng đi qua hai đường thẳng song song thì có thể song song với nhau hoặc cắt nhau
C. Hai đường thẳng nằm trên hai mặt phẳng song song thì có thể song song với nhau hoặc chéo nhau
Đáp án D
Câu 6:
Câu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Có thể sửa lại các câu sai thành các câu đúng như sau.
A. Sửa lại: a//b , b ⊂ (P) và thì a// (P)
B. a//b, b⊂ (P), ; (Q) qua a và (Q) ∩ (P) = c thì c//a
C. (Q) ∩ (P) = a, (R) ∩ (P) = b và a//b thì có thể (R) // (Q) hoặc (R) cắt (Q)
D. a ⊂ (P); b ⊂ (Q) và a chéo b thì có thể (P) // (Q) hoặc (P) cắt (Q)
Đáp án B
Câu 7:
Cho hình chóp S.ABCD, các cặp đường thẳng nào sau đây chéo nhau?
 Xem đáp án
Xem đáp án
SA chéo BD
Đáp án C
Câu 8:
Tìm mệnh đề đúng trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
Có thể sửa lại các câu sai thahf các câu đúng như sau.
A. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì có thể song song, chéo nhau hoặc vuông góc với nhau
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau
C. Một đường thẳng và một mặt phẳng – không chứa đường thẳng đó – cùng vuông góc với một mặt phẳng khác thì song song với nhau
D. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau
Đáp án D
Câu 9:
Tìm mệnh đề đúng trong các mệnh đề sau?
 Xem đáp án
Xem đáp án
Có thể sửa lại các câu sai thành các câu đúng như sau:
A. Đường thẳng a vuông góc với hai đường thẳng b, c cắt nhau nằm trong mặt phẳng (P) thì a vuông góc với (P)
B. Mặt phẳng (P) vuông góc với đường thẳng a nằm trong mặt phẳng (Q) thì (P) vuông góc với (Q)
C. Đường thẳng a vuông góc với hai đường thẳng b, c cắt nhau nằm trong mặt phẳng (P) thì a vuông góc với (P)
D. Đường thẳng a song song với đường thẳng b nằm trong mặt phẳng (P) không chứa a thì a song song với mặt phẳng (P)
Đáp án B
Câu 10:
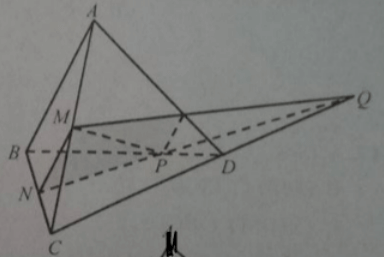
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Giao tuyến của hai mặt phẳng (MNP) và (ACD) là:
 Xem đáp án
Xem đáp án
(MNP) ∩ (ACD) = (MNQ) ∩ (ACD) = MQ.
Đáp án C
Câu 11:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Đường thẳng MP không chéo với đường thẳng nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án C
Câu 12:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Tỉ số QD/QC bằng:
 Xem đáp án
Xem đáp án
Áp dụng định lí Mê-nê-la-uýt:
Đáp án A
Câu 13:
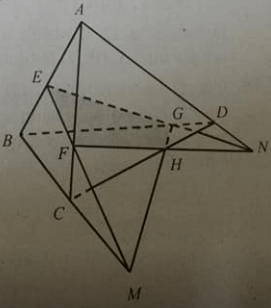
Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên các cạnh AB, AC, BD sao cho EF cắt BC tại M, EG cắt AD tại N. tìm mệnh đề sai trong các mệnh đề sau đây?
 Xem đáp án
Xem đáp án
Trong mặt phẳng (ACD) : FN cắt CD tại H ⇒ H ∈ (EFG) và H ∈ (BCD) ⇒ H ∈ MG là giao tuyến của (EFG) và (BCD) hay FN, MG, CD đồng quy tại H ⇒ M, N, F, G đồng phẳng
Đáp án D
Câu 14:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số IA/IF bằng:
 Xem đáp án
Xem đáp án
Trong mặt phẳng (SAC) : AF ∩S O = I là trọng tâm tam giác SBD ⇒ IA/IF=2
Đáp án B
Câu 15:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số EJ/IF bằng
 Xem đáp án
Xem đáp án
Trong mặt phẳng (ABCD) : BD ∩ EC = K
Trong mặt phẳng (SEC) : EF ∩ SK = J. Áp dụng định lí Me-nê-la-uýt vào tam giác EFC ta được: EJ/JF = 1
Đáp án B
Câu 16:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số IJ/JB bằng:
 Xem đáp án
Xem đáp án
Chứng minh B, J, I thẳng hàng. Áp dụng định lí Mê-nê-la-uýt vào tam giác IAB ta được IJ/JB = 1/4.
Đáp án C
Câu 17:
Cho hình chóp S.ABCD, đáy hình thang ABCD có đáy lớn AD. Trong các mệnh đề sau mệnh đề nào sai?
 Xem đáp án
Xem đáp án
A. (SAC) ∩ (SBD) = SO
B. (SAB) ∩ (SCD) = SE
C. (SAD) ∩ (SBC) = xy
D. nếu S, A, C, D cùng nằm trong một mặt phẳng thì S ∈ (ACD) mâu thuẫn với giả thiết S.ABCD là hình chóp
Đáp án D
Câu 18:
Cho hình tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Thiết diện của tứ diện đi qua ba điểm M, N, P là:
 Xem đáp án
Xem đáp án
Gọi Q là trung điểm AD chứng mình MNPQ là hình bình hành ⇒ M, N, P, Q cùng thuộc một mặt phẳng ⇒ thiết diện là hình bình hành.
Câu 19:
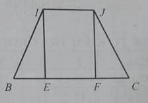
Cho hình chóp S.ABCD đáy là hình vuông ABCD cạnh bằng a, cạnh bên hình chóp cũng bằng a. gọi I là trung điểm của SA. Mặt phẳng (IBC) cắt hình chóp theo thiết diện CBIJ. CBIJ là hình gì (tìm câu đúng nhất)
 Xem đáp án
Xem đáp án
trong mặt phẳng (SAC) : SO ∩ CI = K là trọng tâm tam giác SAC
Trong mặt phẳng (SBD): BK ∩ SD = J là trung điểm SD ⇒ IJ // AD ⇒ IJ // BC.
∆SAB = ∆SCD (c.c.c) ⇒ trung tuyến BI = CJ ⇒ thiết diện CBIJ là hình thang cân.
Đáp án D
Câu 20:
Cho hình chóp S.ABCD đáy là hình vuông ABCD cạnh bằng a, cạnh bên hình chóp cũng bằng a. gọi I là trung điểm của SA. Mặt phẳng (IBC) cắt hình chóp theo thiết diện CBIJ. Chu vi thiết diện CBIJ bằng:
 Xem đáp án
Xem đáp án
Chu vi CBIJ = BC + IJ + 2BI
Đáp án B
Câu 21:
Cho hình chóp S.ABCD đáy là hình vuông ABCD cạnh bằng a, cạnh bên hình chóp cũng bằng a. gọi I là trung điểm của SA. Mặt phẳng (IBC) cắt hình chóp theo thiết diện CBIJ. Diện tích thiết diện CBIJ bằng:
 Xem đáp án
Xem đáp án
Kẻ đường cao IE, JF
Đáp án C
Câu 22:
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là .
Tìm câu đúng nhất.
Thiết diện của hình tứ diện cắt bởi mặt phẳng () là:
 Xem đáp án
Xem đáp án
Gọi I là trung điểm CD thì ⇒ mặt phẳng () chính là mặt phẳng (ABI) ⇒ Thiết diện là tam giác cân AIB.
Đáp án C
Câu 23:
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là . Chu vi thiết diện đó bằng:
 Xem đáp án
Xem đáp án
Chu vi ∆ABI = AB + 2AI = a + 2.(a√3)/2 = a(1 + √3)
Đáp án A
Câu 24:
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là . Diện tích thiết diện đó bằng:
 Xem đáp án
Xem đáp án
BI = (a√3)/2 (đường cao tam giác đều)
Đáp án C
Câu 25:
Tìm kết luận sai.
Cắt hình chóp S.ABCD bởi mặt phẳng (P) thì thiết diện có thể là:
 Xem đáp án
Xem đáp án
Hình chóp S.ABCD có năm mặt nên thiết diện không thể là hình lục giác.
Đáp án D
Câu 26:
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng cạnh bên bằng a. Góc giữa cạnh bên và mặt phẳng đáy bằng:
 Xem đáp án
Xem đáp án
Gọi O là giao điểm của AC và BD.
Vì S, ABCD là hình chóp tứ giác đều nên
Hình chiếu vuông góc của điểm S lên mp(ABCD) là điểm O nên góc giữa cạnh bên và mặt phẳng đáy là góc SBO.
Ta có:
Lại có: nên tam giác SBD vuông cân tại S.
Đáp án C
Câu 27:
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng cạnh bên bằng a.
 Xem đáp án
Xem đáp án
Từ O dựng , suy ra N là trung điểm của BC.
Hai mặt phẳng (SBC) và (ABCD) cắt nhau theo giao tuyến BC
Và
Suy ra:
Ta có:
Tam giác SBC có SB = SC = BC =a nên là tam giác đều ; đường cao
Đáp án C
Câu 28:
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng cạnh bên bằng a. Khoảng cách từ AD tới (SBC) bằng:
 Xem đáp án
Xem đáp án
Gọi O là tâm của hình vuông ABCD , N là trung điểm của BC.
Ta có: AD// BC nên AD// mp(SBC)
d( AD; (SBC)) = d(A; (SBC)) =2.d(O;(SBC)).
* Trong mp( SON) , kẻ OH vuông góc SN. Khi đó, khoảng cách từ O đến (SBC) là OH
Tam giác SBC là tam giác đều đường cao SN nên
Đáp án A
Câu 29:
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng cạnh bên bằng a. Thiết diện của hình chóp đi qua BC và vuông góc với (SDA) là:
 Xem đáp án
Xem đáp án
Thiết diện của hình chóp với mặt phẳng đi qua BC và vuông góc với (SAD) là hình thang cân BCEF.
Đáp án B
Câu 30:
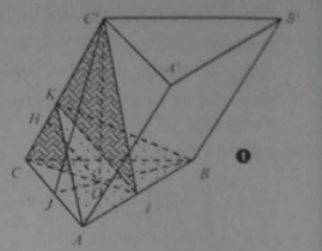
Cho hình lăng trụ ABC.A’B’C’ đáy là tam giác đều tâm O, C’O vuông góc với (ABC). Khoảng cách từ O tới đường thẳng CC’ bằng a. Góc tạo bởi mặt phẳng (AA’C’C) và mp(BB’C’C) bằng . Gọi góc giữa cạnh bên và đáy của lẳng trụ là φ thì.
 Xem đáp án
Xem đáp án
Gọi giao điểm của BO và AC là J; giao điểm của CO và AB là I.
Kẻ AK vuông góc CC’.
Vì đường thẳng CC’ vuông góc mp(ABK ) nên BK vuông góc CC’.
Đáp án C