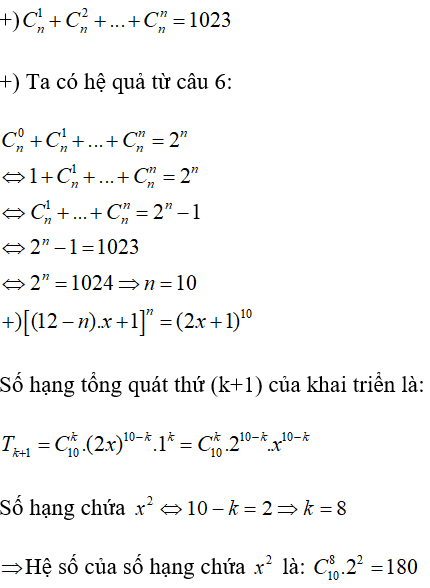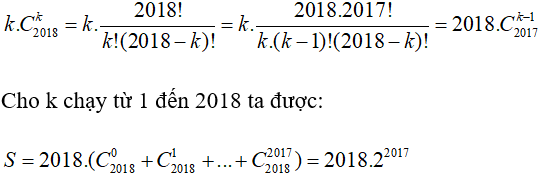11 câu hỏi trắc nghiệm thuộc Trắc nghiệm Nhị thức Niu-tơn có đáp án (Vận dụng)

Câu 1:

Cho n là số nguyên dương thỏa mãn $C_{n}^{0} + 2 C_{n}^{1} + 2^{2} C_{n}^{2} + . . . + 2^{n} = 14348907$ . Hệ số có số hạng chứa $x^{10}$ trong khai triển của biểu thức ${(x^{2} - \frac{1}{x^{3}})}^{n}$ bằng.

A. -1365.

B. 32760.

C. 1365.

D. -32760.

Xem đáp án

Đáp án cần chọn là: C

Câu 2:

Cho $n \in N$ thỏa mãn $C_{n}^{1} + C_{n}^{2} + . . . + C_{n}^{n} = 1023 .$ Tìm hệ số $x^{2}$ trong khai triển ${[(12 - n) x + 1]}^{n}$ thành đa thức.

A. 90.

B. 2.

C. 45.

D. 180.

Xem đáp án

Đáp án cần chọn là: D

Câu 3:

Tổng các hệ số trong khai triển ${(3 x - 1)}^{n} = a_{0} + a_{1} x + a_{2} x^{2} + . . . + a_{n} x^{n}$ là $2^{11}$ . Tìm $a_{6}$ .

A. $a_{6} = - 336798$ .

B. $a_{6} = 336798$ .

C. $a - 112266$ .

D. $a_{6} = 112266$ .

Xem đáp án

Đáp án cần chọn là: A

${(3 x - 1)}^{n} = a_{0} + a_{1} x + a_{2} x^{2} + . . . + a_{n} x^{n}$

Thay x=1 vào 2 vế, ta có: ${(3.1 - 1)}^{n} = a_{0} + a_{1} + a_{2} + . . . + a_{n}$

Mà tổng các hệ số trong khai triển bằng $2^{11}$ nên ${(3 - 1)}^{n} = 2^{11} \Leftrightarrow n = 11$

Số hạng tổng quát của khai triển ${(3 x - 1)}^{11}$ là:

$T_{k + 1} = C_{11}^{k} {(3 x)}^{11 - k} . {(- 1)}^{k} = C_{11}^{k} . 3^{11 - k} {(- 1)}^{k} . x^{11 - k}$

$a_{0}$ là hệ số số hạng chứa $x^{0}$

$a_{1}$ là hệ số số hạng chứa $x^{1}$

...

$a_{6}$ là hệ số số hạng chứa $x^{6}$

$\Rightarrow x^{11 - k} = x^{6} \Rightarrow k = 5$

Hệ số số hạng chứa $x^{6}$ là: $C_{11}^{5} . 3^{6} . {(- 1)}^{5} = - 336798$ .

Câu 4:

Cho n là số nguyên dương thỏa mãn điều kiện $6 C_{n + 1}^{n - 1} = A_{n}^{2} + 160 .$ Tìm hệ số của $x^{7}$ trong khai triển $(1 - 2 x^{3}) {(2 + x)}^{n}$ .

A. -2224.

B. 2224.

C. 1996.

D. -1996.

Xem đáp án

Đáp án cần chọn là: A

Điều kiện: $n \geq 2$

Từ giả thiết, ta có:

$6 C_{n + 1}^{n - 1} = A_{n}^{2} + 160 \Leftrightarrow 6 . \frac{(n + 1)!}{(n - 1)! . 2!} = \frac{n!}{(n - 2)!} + 160 \Leftrightarrow 3 n (n + 1) = n (n - 1) + 160 \Leftrightarrow 2 n^{2} + 4 n - 160 = 0 \Leftrightarrow n = 8 (v ì đ i ề u k i ệ n n \geq 2)$

Khi đó, ta được khai triển $(1 - 2 x^{3}) {(2 + x)}^{8} = {(2 + x)}^{8} - 2 x^{3} {(2 + x)}^{8}$

Theo khai triển nhị thức Newton, ta có:

${(2 + x)}^{8} = \sum_{k = 0}^{8} C_{8}^{k} . 2^{8 - k} . x^{k}$

Suy ra hệ số của $x^{7}$ ứng với k+3=7 $\Leftrightarrow$ k=4

Hệ số của $x^{7}$ trong khai triển $x^{3} {(2 + x)}^{8} l à 2^{4} . C_{8}^{4}$

Vậy hệ số cần tìm là $2 . C_{8}^{7} - 2 . 2^{4} . C_{8}^{4} = - 2224$ .

Câu 5:

Biết tổng các hệ số của khai triển nhị thức ${(x + \frac{1}{x})}^{3 n} = 64$ . Tìm số hạng không chứa x.

A. 13.

B. 14.

C. 15.

D. 16.

Xem đáp án

Đáp án cần chọn là: C

Câu 6:

Cho ${(1 + 2 x)}^{n} = a_{0} + a_{1} x^{1} + . . . + a_{n} x^{x}$ . Biết $a_{0} + \frac{a_{1}}{2} + \frac{a_{2}}{2^{2}} + . . . + \frac{a_{n}}{2^{n}} = 4096 .$ Số lớn nhất trong các số có giá trị bằng.

A. 126720.

B. 924.

C. 972.

D. 1293600.

Xem đáp án

Đáp án cần chọn là: A

Xét ${(1 + 2 x)}^{n} = a_{0} + a_{1} x^{1} + . . . + a_{n} x^{x}$ .

Thay $x = \frac{1}{2}$ vào hai vế

$\Rightarrow {(1 + 2 . \frac{1}{2})}^{n} = a_{0} + a_{1} . {\frac{1}{2}}^{1} + . . . + a_{n} {(\frac{1}{2})}^{n} \Leftrightarrow 2^{n} = 4096 \Leftrightarrow 2^{n} = 2^{12} \Leftrightarrow n = 12$

Biểu thức là: ${(1 + 2 x)}^{12}$

Số hạng tổng quát của khai triển là: $T_{k +!} = C_{12}^{k} . 2^{k} . x^{k}$

Hệ số lớn nhất $\Leftrightarrow y = C_{12}^{k} . 2^{k} m a x (0 \leq k \leq 12)$

Mà hệ số max $\Rightarrow k_{m a x} \Rightarrow$ Muốn k max thì k phải lớn hơn cả số hạng đứng trước nó là (k-1) và lớn hơn cả số hạng đứng sau nó là (k+1)

Ta có hệ

$\{\begin{cases} C_{12}^{k - 1} . 2^{k - 1} < C_{12}^{k} . 2^{k} (1) \\ C_{12}^{k + 1} . 2^{k + 1} < C_{12}^{k} . 2^{k} (2) \end{cases} (1) \Rightarrow \frac{12!}{(k - 1)! (12 - k + 1)!} . \frac{2^{k}}{2} < \frac{12!}{k! (12 - k)!} . 2^{k} \Leftrightarrow \frac{1}{(k - 1)! (13 - k) (12 - k)!} . \frac{1}{2} < \frac{1}{k (k - 1)! (12 - k)!} \Leftrightarrow \frac{1}{2 . (13 - k)} < \frac{1}{k} \Leftrightarrow \frac{1}{13 - k} < \frac{2}{k}$

(2) ta làm tương tự như trên:
$\Rightarrow \frac{2}{k + 1} < \frac{1}{12 - k}$

Từ (1) và (2) $\Rightarrow \{\begin{cases} \frac{1}{13 - k} < \frac{2}{k} \\ \frac{2}{k + 1} < \frac{1}{12 - k} \end{cases}$

$\Leftrightarrow \{\begin{array}{l} k < \frac{26}{3} \\ k > \frac{23}{3} \end{array} \Leftrightarrow \{\begin{array}{l} k < 8, 6 \\ k > 7, 6 \end{array} (M à k l à s ố n g u y ê n) \Rightarrow k = 8$

Hệ số lớn nhất trong khai triển biểu thức là y(8)= $C_{12}^{8} . 2^{8} = 126720 .$

Câu 7:

Tìm hệ số của $x^{5}$ trong khai triển thành đa thức của ${(2 - 3 x)}^{2 n}$ , biết n là số nguyên dương thỏa mãn: $C_{2 n + 1}^{0} + C_{2 n + 1}^{2} + C_{2 n + 1}^{4} + . . . + C_{2 n + 1}^{2 n} = 1024 .$

A. 2099529.

B. -2099520.

C. -1959552.

D. 1959552.

Xem đáp án

Đáp án cần chọn là: C

$C_{2 n + 1}^{0} + C_{2 n + 1}^{2} + C_{2 n + 1}^{4} + . . . + C_{2 n + 1}^{2 n} = 1024 . \Leftrightarrow 2 [C_{2 n + 1}^{0} + C_{2 n + 1}^{2} + C_{2 n + 1}^{4} + . . . + C_{2 n + 1}^{2 n}] = 2.1024$

$\Leftrightarrow (C_{2 n + 1}^{0} + C_{2 n + 1}^{2} + C_{2 n + 1}^{4} + . . . + C_{2 n + 1}^{2 n}) + (C_{2 n + 1}^{0} + C_{2 n + 1}^{2} + C_{2 n + 1}^{4} + . . . + C_{2 n + 1}^{2 n}) = 2.1024 (*)$

Vì $C_{n}^{k} = C_{n}^{n - k} \Rightarrow \{\begin{cases} C_{2 n + 1}^{0} = C_{2 n + 1}^{2 n + 1} \\ C_{2 n + 1}^{1} = C_{2 n + 1}^{2 n} \\ . . . \end{cases}$

$\Rightarrow C_{2 n + 1}^{0} + C_{2 n + 1}^{2} + C_{2 n + 1}^{4} + . . . + C_{2 n + 1}^{2 n} = C_{2 n + 1}^{2 n + 1} + . . . + C_{2 n + 1}^{1}$

(Nói cách khác: Tổng các C có chỉ số chẵn= Tổng các C có chỉ số lẻ)

$(*) \Rightarrow (C_{2 n + 1}^{2 n + 1} + . . . + C_{2 n + 1}^{1}) + (C_{2 n + 1}^{0} + C_{2 n + 1}^{2} + C_{2 n + 1}^{4} + . . . + C_{2 n + 1}^{2 n}) = 2.1024 \Leftrightarrow C_{2 n + 1}^{0} + C_{2 n + 1}^{1} + C_{2 n + 1}^{2} + . . . + C_{2 n + 1}^{2 n} + C_{2 n + 1}^{2 n + 1} = 2048 \Leftrightarrow {(1 + 1)}^{2 n + 1} = 2048 \Leftrightarrow 2^{2 n + 1} = 2024 \Leftrightarrow 2 n + 1 = 11 \Leftrightarrow n = 5$

+) Số hạng tổng quát của khai triển: ${(2 - 3 x)}^{10} l à : T_{k + 1} = C_{10}^{k} . 2^{10 - k} . {(- 3)}^{k} . x^{k}$

Số hạng chứa $x^{5} \Rightarrow x^{5} = x^{k} \Rightarrow k = 5$

Hệ số của số hạng chứa $x^{5}$ là $C_{10}^{5} . 2^{5} . {(- 3)}^{5} = - 1959552$ .

Câu 8:

Tìm số hạng chứa $x^{13}$ trong khai triển thành các đa thức của ${(x + x^{2} + x^{3})}^{10}$ là:

A. 135.

B. 210.

C. $135 x^{13}$ .

D. $210 x^{13}$ .

Xem đáp án

Đáp án cần chọn là: D

Câu 9:

Số nguyên dương n thỏa mãn

$C_{n}^{0} . C_{n + 1}^{n} + C_{n}^{1} . C_{n + 1}^{n - 1} + C_{n}^{2} . C_{n + 1}^{n - 2} + . . . + C_{n}^{n - 1} C_{n + 1}^{n} + C_{n}^{n} . C_{n + 1}^{0} = 1716$

là:

A. n=9.

B. n=7.

C. n=8.

D. n=6.

Xem đáp án

Đáp án cần chọn là: D

Ta có: ${(1 + x)}^{2 n + 1} = C_{2 n + 1}^{0} + C_{2 n + 1}^{1} . x + C_{2 n + 1}^{2} x^{2} + . . . + C_{2 n + 1}^{2 n} . x^{2 n} + C_{2 n + 1}^{2 n + 1} . x^{2 n + 1} (1)$

Mặt khác:

${(1 + x)}^{n} = C_{n}^{0} + C_{n}^{1} x + C_{n}^{2} x^{2} + . . . + C_{n}^{n - 1} x^{n - 1} + C_{n}^{n} x^{n} {(1 + x)}^{n + 1} = C_{n + 1}^{0} + C_{n + 1}^{1} x + C_{n + 1}^{x} x^{2} + . . . + C_{n + 1}^{n - 1} x^{n - 1} + C_{n + 1}^{n} x^{n} + C_{n + 1}^{n + 1} x^{n + 1}$

Suy ra:

${(1 + x)}^{n} . {(1 + x)}^{n + 1} = (C n 0 + C n 1 x + C n 2 . x)$ ²+...+Cnnxⁿ.Cn+10+Cn+11x+...+Cn+1n+1xⁿ⁺¹(2)

Từ (1) và (2), đồng nhất hệ số của $x^{n}$ ta được:

$C_{n}^{0} . C_{n + 1}^{n} + C_{n}^{1} . C_{n + 1}^{n - 1} + . . . + C_{n}^{n - 1} . C_{n + 1}^{n} + C_{n}^{n} . C_{n + 1}^{0} = C_{2 n + 1}^{n}$

Với n=9 ta có: $C_{2 n + 1}^{n} = C_{19}^{9} = 92378 .$

Với n=8 ta có: $C_{2 n + 1}^{n} = C_{17}^{8} = 24310 .$

Với n=7 ta có: $C_{2 n + 1}^{n} = C_{15}^{7} = 6435 .$

Với n=6 ta có: $C_{2 n + 1}^{n} = C_{13}^{6} = 1716 .$

Câu 10:

Rút gọn tổng sau: $S = C_{n}^{1} + 2 C_{n}^{2} + 3 C_{n}^{3} + . . . + n C_{n}^{n}$ ta được:

A. $S = n . 2^{n}$ .

B. $2^{n + 1}$ .

C. $n . 2^{n - 1}$ .

D. $2^{n - 1}$ .

Xem đáp án

Đáp án cần chọn là: C

Câu 11:

Tính tổng $S = 1 . C_{2018}^{1} + 2 . C_{2018}^{2} + 3 . C_{2018}^{3} + . . . + 2018 C_{2018}^{2018}$ .

A. $2018 . 2^{2017} .$

B. $2017 . 2^{2018}$ .

C. $2018 . 2^{2018}$ .

D. $2017 . 2^{2017}$ .

Xem đáp án

Đáp án cần chọn là: A

Trắc nghiệm Nhị thức Niu-tơn có đáp án (Vận dụng)

Trắc nghiệm Nhị thức Niu-tơn có đáp án (Vận dụng)

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương