12 câu hỏi trắc nghiệm thuộc Trắc nghiệm Hai đường thẳng vuông góc với nhau có đáp án

Câu 1:

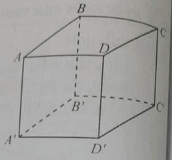
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng AC và C’D’ bằng:

A. $0^{o}$

B. $45^{o}$

C. $60^{o}$

D. $90^{o}$

Xem đáp án

Vì CD // C’D’ nên góc giữa AC và C’D’ bằng góc giữa AC và CD và bằng $\hat{A C D}$

Vì ABCD là hình vuông nên tam giác ACD vuông cân tại D

$\Rightarrow \hat{A C D} = 45^{0}$

Đáp án B

Câu 2:

Khẳng định nào sau đây đúng?

A. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.

B. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.

C. Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

D. Hai đường thẳng cùng song song với đường thẳng thứ ba thì vuông góc với nhau.

Xem đáp án

phương án A và B sai vì hai đường thẳng cùng vuông góc với đường thẳng thứ ba có thể cắt nhau hoặc chéo nhau.

Phương án C đúng vì hai đường thẳng cùng song song với đường thẳng thứ ba thì phương của chúng song song với nhau.

Phương án D sai vì hai đường thẳng cùng song song với đường thẳng thứ ba thì có thể song song hoặc trùng nhau.

Đáp án C

Câu 3:

Cho tứ diện ABCD có AB = AC = AD; góc BAC = góc $B A D = 60^{o}$ . Hãy chứng minh AB ⊥ CD.

Một bạn chứng minh qua các bước sau:

Bước 1. $\vec{C D} = \vec{A C} - \vec{A D}$

Bước 2. $\vec{A B} . \vec{C D} = \vec{A B} . (\vec{A C} - \vec{A D})$

Bước 3. $\vec{A B} . \vec{A C} - \vec{A B} . \vec{A D} = | \vec{A B} | . | \vec{A D} | . \cos 60^{o} - | \vec{A B} | . | \vec{A D} | . \cos 60^{o} = 0$

Bước 4. Suy ra AB ⊥ CD

Theo em. Lời giải trên sai từ:

A. bước 1

B. bước 2

C. bước 3

D. bước 4

Xem đáp án

Đáp án A

Lời giải trên sai từ bước 1 vì $\vec{C D} = \vec{A D} - \vec{A C} \neq \vec{A C} - \vec{A D}$

Câu 4:

Cho tứ diện ABCD có tam giác ABC và ACD là tam giác đều .

Gọi M, N , P lần lượt là trung điểm của BC; BD và AB. Tính góc giữa hai đường thẳng DM và MN ?

A. $45^{0}$

B. $60^{0}$

C. $90^{0}$

D. $30^{0}$

Xem đáp án

Xét tam giác ABC có MP là đường trung bình nên MP// AC. (1)

Xét tam giác BCD có MN là đường trung bình nên MN// CD (2)

Từ (1) và (2) suy ra: (MP; MN) = (AC; CD) = $\hat{A C D} = 60^{0}$

Chọn B.

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và tam giác SAD vuông cân tại A. Xác định góc giữa hai đường thẳng SD và BC

A. $30^{0}$

B. $60^{0}$

C. $90^{0}$

D. $45^{0}$

Xem đáp án

Vì đáy ABCD là hình bình hành nên AD// BC

Khi đó; ( SD; BC) = ( SD; AD)= $\hat{S D A}$ (1)

Vì tam giác SAD là tam giác vuông cân tại A nên $\hat{A D S} = 45^{0}$ (2)

Vậy góc giữa hai đường thẳng SD và BC là $45^{0}$

Câu 6:

Nếu ba vecto $\vec{a}, \vec{b}, \vec{c}$ cùng vuông góc với vecto $\vec{n}$ khác $\vec{0}$ thì chúng.

A. đồng phẳng

B. không đồng phẳng

C. có thể đồng phẳng

D. có thể không đồng phẳng

Xem đáp án

Đáp án A

Câu 7:

Các đường thẳng cùng vuông góc với một đường thẳng thì:

A. thuộc một mặt phẳng

B. vuông góc với nhau

C. song song với một mặt phẳng

D. song song với nhau

Xem đáp án

Phương án A sai vì có thể xảy ra trường hợp chúng nằm trên nhiều mặt phẳng khác nhau

Phương án B sai vì có thể xảy ra trường hợp chúng song song với nhau

Phương án D sai vì có thể xảy ra trường hợp chúng cắt nhau

Phương án C đúng vì chúng đồng phẳng

Đáp án C

Câu 8:

Cho hình tứ diện đều OABC độ dài cạnh bằng a có OA; OB; OC đôi một vuông góc. Gọi M; N: P; Q lần lượt là trung điểm của OB; OC; AB; AC. Tính tích vô hướng $\vec{P M} . \vec{C N}$

A. 0

B. a

C. $a^{2}$

D. $2 a^{2}$

Xem đáp án

* Xét tam giác OAB có P; M lần lượt là trung điểm của OB; AB nên MP là đường trung bình của tam giác OAB

Suy ra: MP// OA và MP= 1/2 OA

Do đó; $\vec{P M} = \frac{1}{2} \vec{A O}$

* vì N là trung điểm của OC nên: $\vec{C N} = \frac{1}{2} \vec{C O}$

Suy ra: $\vec{P M} . \vec{C N} = \frac{1}{2} . \vec{A O} . \frac{1}{2} \vec{C O} = 0$

( vì AO vuông góc CO)

Chọn A

Câu 9:

Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc tại đỉnh B đều bằng $60^{o}$ .

Đường thẳng B’C vuông góc với đường thẳng:

A.

B. 0

C. BD

D. A’A

Xem đáp án

Phương án A sai vì tam giác ACB’ có ba cạnh bằng a

Phương án C sai vì tam giác CB’D’ có ba cạnh a, a√3,a√3 nên không thể vuông tại B’

Phương án D sai vì góc giữa đường thẳng B’C và AA’ bằng $0^{o}$

Phương án B đúng vì:

$\vec{C B'} . \vec{C D} = (\vec{C C'} + \vec{C' B'}) . \vec{C D} = \vec{C C'} . \vec{C D} + \vec{C' B'} . \vec{C D} = C C' . C D . \cos \hat{C' C D} + C' B' . C D . \cos \hat{B C D} = a . a . \cos 60^{0} + a . a . \cos (180^{0} - \hat{A B C}) = \frac{a^{2}}{2} - \frac{a^{2}}{2} = 0$

Đáp án B

Câu 10:

Cho tứ diện ABCD. Nếu AB ⊥CD, AC ⊥ BD và BC ⊥ AD thì:

A. $\vec{A B} . \vec{A C} \neq \vec{A C} . \vec{A D} = \vec{A B} . \vec{A D}$

B. $\vec{A B} . \vec{A C} = \vec{A C} . \vec{A D} \neq \vec{A B} . \vec{A D}$

C. $\vec{A B} . \vec{A C} = \vec{A C} . \vec{A D} = \vec{A B} . \vec{A D}$

D. $\vec{A B} . \vec{A C} \neq \vec{A C} . \vec{A D} \neq \vec{A B} . \vec{A D}$

Xem đáp án

Ta có: $\vec{A B} . \vec{C D} = \vec{A C} . \vec{B D} = \vec{A D} . \vec{C B} = 0$

⇒ $\vec{A B} (\vec{A D} - \vec{A C}) = \vec{A C} (\vec{A D} - \vec{A B}) = \vec{A D} (\vec{A B} - \vec{A C}) = 0$

⇒ $\vec{A B} . \vec{A C} = \vec{A C} . \vec{A D} = \vec{A B} . \vec{A D}$

Đáp án C

Câu 11:

Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng $60^{o}$ . Gọi M và N là trung điểm của AB và CD

Góc giữa $\vec{A B}$ và $\vec{C D}$ bằng:

A. $30^{o}$

B. $60^{o}$

C. $90^{o}$

D. $120^{o}$

Xem đáp án

Ta có: $\vec{A B} . \vec{C D} = \vec{A B} (\vec{A D} - \vec{A C})$ $= \vec{A B} . \vec{A D} - \vec{A B} . \vec{A C}$

$= |\vec{A B}| . |\vec{A D}| . \cos \hat{B A D} - |\vec{A B}| . |\vec{A C}| \cos \hat{B A C}$

$= A B^{2} . \cos 60 ° - A B^{2} \cos 60 °$ (do AB = AC = AD và $\hat{B A C} = \hat{B A D} = 60 °$ )

= 0

Suy ra $A B ⊥ C D$ hay góc giữa hai vecto $\vec{A B}$ và $\vec{C D}$ là $90 °$ .

ĐÁP ÁN C

Câu 12:

Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng $60^{o}$ . Gọi M và N là trung điểm của AB và CD

Kết luận nào sau đây sai?

A. MN vuông góc với AB

B. MN vuông góc với CD

C. MN vuông góc với AB và CD

D. MN không vuông góc với AB và CD

Xem đáp án

Tam giác ABD có AB = AD và $\hat{B A D} = 60 °$

Nên tam giác ABD đều $\Rightarrow D M = \frac{A B \sqrt{3}}{2}$ (DM là trung tuyến)

Tam giác ABC có AB = AC và $\hat{B A C} = 60 °$

Nên tam giác ABC đều $\Rightarrow C M = \frac{A B \sqrt{3}}{2}$ (CM là trung tuyến)

Do đó: DM = CM nên tam giác MCD cân tại M có MN là trung tuyến (do N là trung điểm của CD)

Suy ra MN là đường cao của tam giác MCD

$\Rightarrow M N ⊥ C D$

Chứng minh tương tự:

Vì hai tam giác ACD và BCD bằng nhau (c.c.c) nên hai đường trung tuyến tương ứng AN; BN bằng nhau:

AN = BN

Suy ra:tam giác ABN cân tại N có NM là đường trung tuyến nên

$M N ⊥ A B$

Vậy kết luận D là kết luận sai

Đáp án D

Trắc nghiệm Hai đường thẳng vuông góc với nhau có đáp án

Trắc nghiệm Hai đường thẳng vuông góc với nhau có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương