6 câu hỏi trắc nghiệm thuộc Trắc nghiệm Bội chung và bội chung nhỏ nhất có đáp án ( Thông hiểu )

Trắc nghiệm Bội chung và bội chung nhỏ nhất có đáp án ( Thông hiểu )

Đề số 1

Trắc nghiệm Bội chung và bội chung nhỏ nhất có đáp án ( Thông hiểu )

67 lượt thi
6 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Viết tập hợp các số tự nhiên nhỏ hơn 40 là bội chung của 6 và 9 là:

A.{0; 18; 36; 54; .....}

B.{0; 12; 18; 36}

C.{0; 18; 36}

D.{0; 18; 36; 54}

Các bội của 6 là: 0; 6; 12; 18; 24; 30; 36; 42; 48; 54; ...

Các bội của 9 là: 0; 9; 18; 27; 36; 45; 54...

Do đó: BC(6, 9) = {0; 18; 36; 54; ...}

Từ đó, ta thấy các số tự nhiên nhỏ hơn 40 là bội chung của 6 và 9 là: 0; 18; 36.

Ta viết được tập hợp như sau: {0; 18; 36}.

Chọn đáp án C.

Câu 2:

Viết tập hợp các bội chung của 4 và 6 nhỏ hơn 35 là:

A.{0; 12; 24}

B.{0; 12; 24; 36}

C.{12; 24}

D.{12; 24; 36}

Các bội của 4 là: 0; 4; 8; 12; 16; 20; 24; 28; 32; 36; ....

Các bội của 6 là: 0; 6; 12; 18; 24; 30; 36; ...

Do đó: BC(4, 6) = {0; 12; 24; 36; ....}

Các bội chung của 4 và 6 nhỏ hơn 35 là: 0; 12; 24.

Vậy ta viết tập hợp: {0; 12; 24}.

Chọn đáp án A.

Câu 3:

Gọi A là tập hợp các ước của 36, B là tập hợp các bội của 6. Viết tập hợp C các số vừa thuộc tập hợp A vừa thuộc tập hợp B.

A.{0; 6; 12}

B.{6; 12; 18}

C.{6; 12; 18; 36}

D.{0; 6; 18; 36}

Các ước của 36 là: 1; 2; 3; 4; 6; 9; 12; 18; 36.

Do đó ta viết tập hợp A là: A = {1; 2; 3; 4; 6; 9; 12; 18; 36}.

Các bội của 6 là: 0; 6; 12; 18; 24; 30; 36; ...

Do đó ta viết tập hợp B là: B = {0; 6; 12; 18; 24; 30; 36; ...}.

Ta thấy các số vừa thuộc tập hợp A, vừa thuộc tập hợp B là: 6; 12; 18; 36.

Do đó ta viết tập hợp C là: C = {6; 12; 18; 36}.

Chọn đáp án C.

Câu 4:

Số tự nhiên a nhỏ nhất khác 0 thỏa mãn a ⁝ 18 và a ⁝ 40.

A.360

B.400

C.458

D.500

Vì a là số tự nhiên nhỏ nhất khác 0 thỏa mãn a ⁝ 18 và a ⁝ 40 nên a = BCNN(18, 40)

Ta có:

18 = 2 . 3²

40 = 2³. 5

Do đó: BCNN(18, 40) = 2³. 3². 5 = 360

Chọn đáp án A.

Câu 5:

Trong các khẳng định sau, khẳng định nào đúng?

A.BCNN của a và b là số nhỏ nhất trong tập hợp bội chung của a và b

B.BCNN(a, b, 1) = BCNN(a, b)

C.Nếu m ⁝ n thì BCNN(m, n) = n

D.Nếu ƯCLN(x, y) = 1 thì BCNN(x, y) = 1

Đáp án A. Sai. Vì BCNN của a và b là số nhỏ nhất khác 0 trong tập hợp bội chung của a và b.

Đáp án B. Đúng. Vì mọi số tự nhiên đều là bội của 1, do đó BCNN(a, b, 1) = BCNN(a, b).

Đáp án C. Sai. Nếu m ⁝ n thì BCNN(m, n) = m.

Đáp án D. Sai. Nếu ƯCLN(x, y) = 1 thì BCNN(x, y) = x . y.

Chọn đáp án B.

Câu 6:

Thực hiện phép tính

được kết quả là:

A.

B.

C.

D.

Để thực hiện được phép tính trên, ta cần quy đồng mẫu số với mẫu số chung là BCNN(5, 12, 15)

Ta có: 12 = 2². 3; 15 = 3 . 5

Do đó BCNN(5, 12, 15) = 2². 3 . 5 = 60

Ta có: 60 : 5 = 12; 60 : 12 = 5; 60 : 15 = 4

Khi đó: ; ;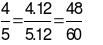

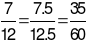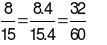
Do đó: = = .

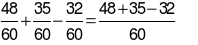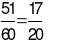Chọn đáp án A.

Bắt đầu thi ngay

Có thể bạn quan tâm

Các bài thi hot trong chương