Trắc nghiệm Bội chung và bội chung nhỏ nhất có đáp án ( Vận dụng )
Trắc nghiệm Bội chung và bội chung nhỏ nhất có đáp án ( Vận dụng )
-
53 lượt thi
-
5 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Vì x ⁝ 12; x ⁝ 28; x ⁝ 36
Do đó x là bội chung 12; 28 và 36.
Ta tìm bội chung của 3 số trên bằng cách tìm bội chung nhỏ nhất.
Ta có: 21 = 3 . 7
28 = 22. 7
36 = 22. 32
Do đó: BCNN(21, 28, 36) = 22. 32. 7 = 252
Các bội của 252 là: 0; 252; 504; …
Suy ra BC(21, 28, 36) = {0; 252; 504; ...}
Vì 150 < x < 300 nên x = 252.
Chọn đáp án C.
Câu 2:
Xem đáp án
Gọi x là số học sinh lớp 6A,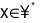 
.
Vì khi xếp hàng 2, hàng 3, hàng 6, hàng 8 đều vừa đủ hàng nên
x ⁝ 2, x ⁝ 3, x ⁝ 6, x ⁝ 8
Do đó x là bội chung của 2; 3; 6 và 8.
Ta có:
6 = 2 . 3
8 = 23
Do đó: BCNN(2, 3, 6, 8) = 23. 3 = 24
Suy ra BC(2, 3, 6, 8) = B(24) = {0; 24; 48; 72; ...}
Vì 40 < x < 60
Do đó: x = 48.
Chọn đáp án A.
Câu 3:
Xem đáp án
Gọi số tự nhiên cần tìm là x.
Vì x ⁝ 3, x ⁝ 4, x ⁝ 5
Do đó x là bội chung của 3; 4; 5.
Vì ƯCLN(3, 4, 5) = 1 nên BCNN(3, 4, 5) = 3 . 4 . 5 = 60.
BC(3, 4, 5) = B(60) = {0; 60; 120; 180; ....}
Vì x là số tự nhiên nhỏ nhất có ba chữ số thỏa mãn x ⁝ 3, x ⁝ 4, x ⁝ 5 nên x = 120.
Chọn đáp án B.
Câu 4:
Xem đáp án
Gọi số ngày phải tìm là x,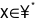 
Khi đó, theo đề bài thì ta thấy x = BCNN(9, 12)
Ta có:
9 = 32
12 = 22. 3
Do đó: BCNN(9, 12) = 22. 32= 36 hay x = 36 (t/m).
Vậy sau ít nhất 36 ngày hai bạn sẽ gặp lại nhau.
Chọn đáp án C.
Câu 5:
Xem đáp án
Vì ƯCLN(a, b) = 36 nên ta đặt a = 36x, b = 36y với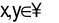 
; ƯCLN (x, y) = 1.
Suy ra BCNN(a, b) = 36x.y = 900 = 36 . 25
Do đó: x . y = 25 = 5 . 5 = 25 . 1
Từ đó, ta có:
TH1: x = 25, y = 1
Khi đó: a = 900, b = 36
TH2: x = 1, y = 25
Khi đó a = 900, b = 36
TH3: x = 5, y = 5 (Không thỏa mãn điều kiện vì ƯCLN(x, y) = 5)
Do đó, không tồn tại a, b.
Vậy có 2 cặp số (a, b) thỏa mãn điều kiện đầu bài là (900, 36) và (36, 900).
Chọn đáp án A.