Đề thi Học kì 1 Toán 10 - Bộ sách KNTT - Đề 02
-
3881 lượt thi
-
38 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
A. Câu trên không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.
B. Câu trên không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.
C. Câu trên không phải là mệnh đề vì nó là câu cảm thán và không khẳng định tính đúng sai.
D. Câu này là mệnh đề vì nó khẳng định tính đúng sai.
Câu 2:
Cho tập hợp A = {2; 4; 6; 8}. Số tập con của tập hợp A là?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Cách 1:
Ta có:
+ Các tập con có 0 phần tử: ∅.
+ Các tập con có 1 phần tử: {2}, {4}, {6}, {8}.
+ Các tập con có 2 phần tử: {2; 4}, {2; 6}, {2; 8}, {4; 6}, {4; 8}, {6; 8}.
+ Các tập con có 3 phần tử: {2; 4; 6}, {2; 4; 8}, {2; 6; 8}, {4; 6; 8}.
+ Các tập con có 4 phần tử: {2; 4; 6; 8}.
Vậy tập hợp A có 16 tập con.
Cách 2: Tập hợp A có 4 phần tử nên số tập con của tập hợp A là 24 = 16.
Câu 3:
Cho tập hợp K = [1 ; 7) \ (– 3 ; 5). Khẳng định nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Tập hợp K là tập hợp các phần tử thuộc [1; 7) nhưng không thuộc (– 3; 5).
Ta xác định tập hợp K bằng cách vẽ trục số như sau: Trên cùng một trục số, tô đậm khoảng [1; 7) và gạch bỏ khoảng (–3; 5), sau đó bỏ luôn các khoảng chưa được tô hoặc đánh dấu. Phần tô đậm không bị gạch bỏ chính là tập hợp K.

Vậy K = [1 ; 7) \ (– 3 ; 5) = [5 ; 7).
Câu 4:
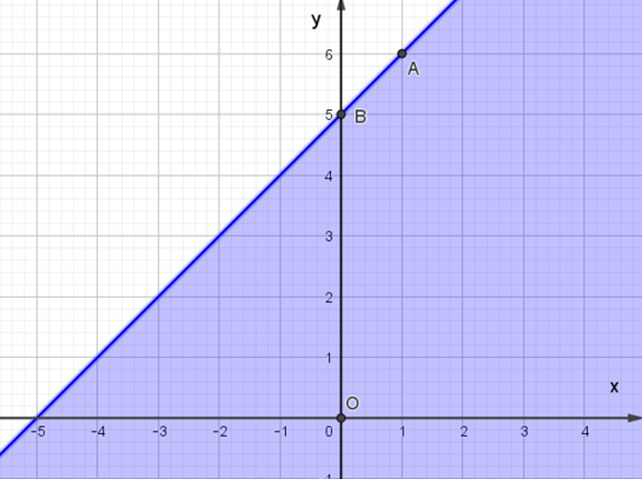
Miền nghiệm của bất phương trình x – y + 5 ≥ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
– Trên mặt phẳng Oxy vẽ đường thẳng Δ: x – y + 5 = 0 đi qua hai điểm A(1; 6) và B(0; 5).
– Xét gốc tọa độ O(0; 0). Ta thấy O không nằm trên đường thẳng Δ và 0 – 0 + 5 ≥ 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng có kể bờ Δ, chứa gốc tọa độ O (miền màu xanh trong hình ảnh).
Câu 5:
Cặp số nào sau đây là nghiệm của hệ bất phương trình bậc nhất hai ẩn {2x−1>0x+5y<4 ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét từng phương trình của hệ {2x−1>0x+5y<4 hay {2x−1>0x+5y−4<0với cặp số (1; –1) ta có:
2.1 – 1 = 1 > 0
1 + 5.(–1) – 4 = –8 < 0
Do đó, cặp số (1; –1) là một nghiệm của hệ bất phương trình bậc nhất hai ẩn {2x−1>0x+5y<4 .
Câu 6:
Chọn phương án SAI trong các phương án dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có:
sin 0° = 0;
cos 90° = 0;
cos 0° = 1;
sin 90° = 1 nên đáp án D sai.
Câu 7:
Cho β là góc tù. Tìm khẳng định đúng trong các khẳng định dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì β là góc tù nên sin β > 0, cos β < 0 , tan β < 0, cot β < 0.
Vậy B đúng, A, C, D sai.
Câu 8:
Cho góc α thỏa mãn sinα=1213 và 90° < α < 180°. Tính cosα.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì 90° < α < 180° nên cosα < 0.
Do đó cosα=−√1−sin2α=−√1−(1213)2=−√25169=−513.
Câu 9:
Cho tam giác ABC biết sinBsinC=√3 và AB=2√2. Tính AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Áp dụng định lý sin trong tam giác ABC, ta có
bsinB=csinC⇔sinBsinC=bc=ACAB
Từ sinBsinC=√3 suy ra ACAB=√3⇔AC=AB√3=2√2.√3=2√6.
Câu 10:
Cho hình bình hành ABCD có K là giao điểm hai đường chéo như hình vẽ.
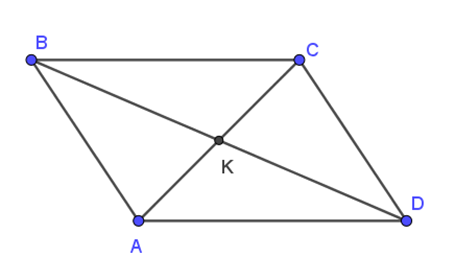
Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
→KC có giá là đường thẳng AC, hướng từ trái sang phải
→KA có giá là đường thẳng AC, hướng từ phải sang trái
Do đó, →KC và →KA cùng phương ngược hướng.
Câu 11:
Cho hình bình hành ABCD có AB = 4 cm. Tính độ dài vectơ →CD.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
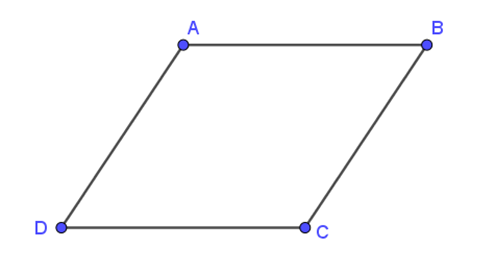
Xét hình bình hành ABCD có:
CD = AB = 4 cm.
Vậy |→CD|=CD=4cm.
Câu 12:
Cho các điểm A, B, C phân biệt. Đẳng thức nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Áp dụng tính chất giao hoán và quy tắc ba điểm cho ba điểm A, C, B ta có: →CB+→AC=→AC+→CB=→AB
Vậy →AB=→CB+→AC.
Câu 13:
Cho hình bình hành ABCD với giao điểm hai đường chéo là I. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
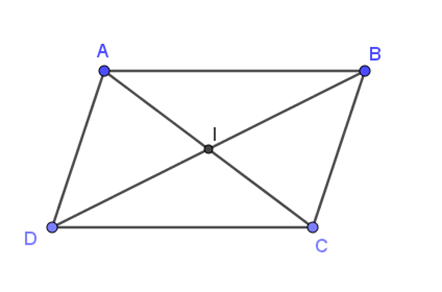
+) Ta có: →AB−→AI=→IB≠→BI nên A sai.
+) →AB−→DA=→AB+→AD=→AC≠→BD (theo quy tắc hình bình hành) nên B sai.
+) Ta có: →AB−→DC=→AB+→CD
Mà →BA=→CD (do ABCD là hình bình hành)
Vậy →AB−→DC=→AB+→CD=→AB+→BA=→AA=→0. Nên C đúng.
+) Ta có: →AB−→DB=→AB+→BD=→AD≠→0. Vậy D sai.
Câu 14:
Cho hình vuông ABCD cạnh 2a. Tính |→AB−→DA|.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
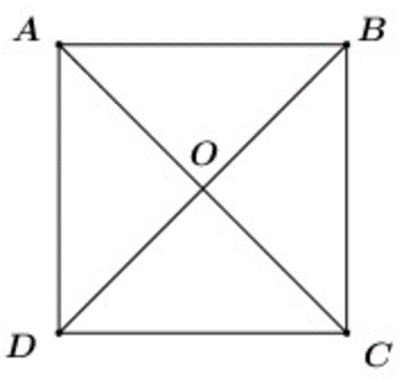
Ta có: →AB−→DA=→AB+→AD=→AC (áp dụng quy tắc hình bình hành cho hình vuông ABCD).
Xét tam giác ADC vuông tại D
Áp dụng định lý Pythagore ta có:
AC2 = AD2 + DC2 = (2a)2 + (2a)2 = 8a2 ⇒ AC = 2a√2
Vậy |→AB−→DA|=2a√2.
Câu 15:
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
→OA+→OB+→OC+→OD
=(→OA+→OB)+(→OC+→OD)
=2→OE+2→OF (do E, F lần lượt là trung điểm của AB, CD)
=2(→OE+→OF)=2.→0=→0 (do O là trung điểm của EF).
Vậy →OA+→OB+→OC+→OD=→0.
Câu 16:
Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích →AN qua các vectơ →a và →b ta được biểu thức là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
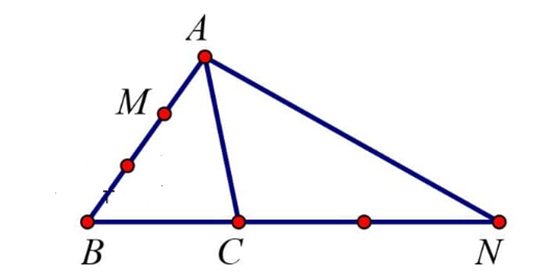
Theo đề bài: CN = 2BC nên →BN=3→BC
Ta có:
→AN=→AB+→BN=→AB+3→BC=→AB+3(→AC−→AB)=−2→AB+3→AC=−2→a+3→b.
Câu 17:
Cho các vectơ →a và →b không cùng phương và →x=→a−3→b, →y=2→a+6→b và →z=−3→a+→b. Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
→x=→a−3→b
→y=2→a+6→b=−2(→a−3→b)=−2→x
Vì – 2 < 0
Vậy →y, →x cùng phương, ngược hướng.
Câu 18:
Cho tam giác ABC có điểm I nằm trên cạnh AC sao cho →BI=34→AC−→AB, J là điểm thỏa mãn →BJ=12→AC−23→AB. Ba điểm nào sau đây thẳng hàng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: →BJ=12→AC−23→AB
→BI=34→AC−→AB=32.12→AC−32.23→AB=32(12→AC−23→AB)=32→BJ
Do đó, →BI=32→BJ
Vậy B, I, J thẳng hàng.
Câu 19:
Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính (→CB,→CA).
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
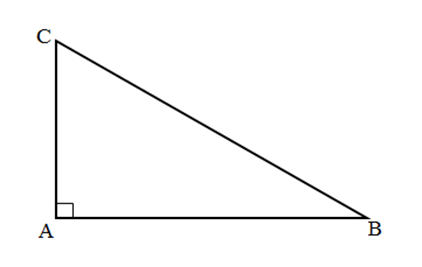
Xét tam giác ABC vuông tại A có:
sin^ACB=ABBC=48=12⇒^ACB=30∘
Vậy (→CB,→CA)=^ACB=30∘.
Câu 20:
Cho hai vectơ →a và →b đều khác →0. Biết: (→a,→b)=30∘, →a.→b=√3và |→b|=2. Tính độ dài của vectơ →a.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
→a.→b=√3⇔|→a|.|→b|.cos(→a,→b)=√3⇔|→a|.2.cos30∘=√3
⇔|→a|.2.√32=√3⇔|→a|=1.
Câu 21:
Cho tam giác ABC đều cạnh a. Tính →AB.→AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Do tam giác ABC đều nên:
AB = AC = a ⇒|→AB|=|→AC|=a
(→AB,→AC)=^BAC=60∘⇒cos^BAC=12.
Ta có:
→AB.→AC=|→AB|.|→AC|.cos^BAC=a.a.12=12a2.
Câu 22:
Cho hình thang ABCD với hai đáy là AB, CD có: (→AB−→AD).→AC=0. Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
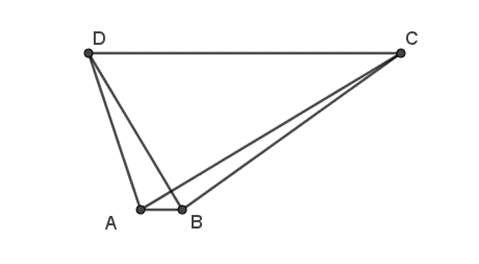
Ta có:
(→AB−→AD).→AC=0⇔→DB.→AC=→0⇔→DB⊥→AC
Vậy BD vuông góc với AC.
Câu 23:
Cho giá trị gần đúng của 617 là 0,35. Sai số tuyệt đối của số gần đúng 0,35 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Sử dụng máy tính cầm tay, ta tính được: 617=0,3529411765....
Ta có: ∆0,35 = |0,35 – 617| < |0,35 – 0,353| = 0,003.
Do đó sai số tuyệt đối của số gần đúng 0,35 không vượt quá 0,003.
Câu 24:
Hãy viết số quy tròn của số gần đúng a = 15,318 biết ¯a = 15,318 ± 0,05.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hàng lớn nhất của độ chính xác d = 0,05 là hàng phần trăm nên ta quy tròn a đến hàng phần mười.
Vậy số quy tròn của a là 15,3.
Câu 25:
Số lượng khách từ ngày thứ nhất đến ngày thứ 10 của một nhà hàng mới mở được thống kê ở bảng sau:
|
Ngày |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số khách |
11 |
9 |
7 |
5 |
15 |
20 |
9 |
6 |
17 |
13 |
Tính số khách trung bình từ bảng số liệu trên.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có cỡ mẫu của mẫu số liệu trên là n = 10.
Số trung bình của mẫu số liệu là:
¯x=11+9+7+5+15+20+9+6+17+1310=11,2.
Câu 26:
Tìm trung vị của mẫu số liệu sau:
1; 0; 5; 10; 2; 3; 9.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Sắp xếp mẫu số liệu trên theo thứ tự không giảm, ta được:
0; 1; 2; 3; 5; 9; 10.
Vì cỡ mẫu là n = 7 nên trung vị của mẫu số liệu trên là số liệu thứ 4. Tức là
Me = 3.
Câu 27:
Cho mẫu số liệu sau:
1; 9; 12; 10; 2; 9; 15; 11; 20; 17.
Tứ phân vị Q1, Q2, Q3 của mẫu số liệu trên lần lượt là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Sắp xếp mẫu số liệu trên theo thứ tự không giảm, ta được:
1; 2; 9; 9; 10; 11; 12; 15; 17; 20.
+ Vì cỡ mẫu là n = 10 nên giá trị tứ phân vị thứ hai là trung bình cộng của số liệu thứ 5 và 6.
Q2 = 10+112=10,5.
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 1; 2; 9; 9; 10.
Do đó Q1 = 9.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 11; 12; 15; 17; 20.
Do đó Q3 = 15.
Vậy tứ phân vị Q1, Q2, Q3 của mẫu số liệu trên lần lượt là 9; 10,5; 15.
Câu 28:
Cho mẫu số liệu sau:
2; 5; 9; 12; 15; 5; 20.
Tìm mốt của mẫu số liệu trên.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta thấy số 5 xuất hiện với tần số nhiều nhất trong mẫu số liệu trên (2 lần).
Vậy M0 = 5.
Câu 29:
Cho mẫu số liệu sau:
15; 26; 5; 2; 9; 5; 28; 30; 2; 26.
Tính khoảng biến thiên của mẫu số liệu trên.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Sắp xếp mẫu số liệu trên theo thứ tự không giảm ta có:
2; 2; 5; 5; 9; 15; 26; 26; 28; 30.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 2.
+ Giá trị lớn nhất của mẫu số liệu trên là 30.
Ta có : R = 30 – 2 = 28.
Do đó khoảng biến thiên của mẫu số liệu trên là 28.
Câu 30:
Cho mẫu số liệu sau:
2; 9; 12; 16; 3; 5; 12; 33; 24; 27.
Tính khoảng tứ phân vị của mẫu số liệu trên.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Sắp xếp mẫu số liệu trên theo thứ tự không giảm ta có:
2; 3; 5; 9; 12; 12; 16; 24; 27; 33.
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 2; 3; 5; 9; 12.
Do đó Q1 = 5.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 12; 16; 24; 27; 33.
Do đó Q3 = 24.
Ta có : ∆Q = Q3 – Q1 = 24 – 5 = 19.
Do đó khoảng tứ phân vị của mẫu số liệu trên là 19.
Câu 31:
Cho mẫu số liệu sau:
12; 2; 6; 13; 9; 21.
Tìm phương sai của mẫu số liệu trên (làm tròn đến hàng phần trăm).
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Số trung bình của mẫu số liệu trên là:
¯x=12+2+6+13+9+216=10,5.
Công thức tính phương sai của một mẫu số liệu là:
S2 = \(\frac{1}{n}\left[ {{{\left( {{x_1} - \overline x } \right)}^2} + {{\left( {{x_2} - \overline x } \right)}^2} + ... + {{\left( {{x_n} - \overline x } \right)}^2}} \right]\)
Thay số ta có:
S2 = 16[(12 – 10,5)2 + (2 – 10,5)2 + (6 – 10,5)2 + (13 – 10,5)2 + (9 – 10,5)2 + (21 – 10,5)2] ≈ 35,58.
Do đó phương sai của mẫu số liệu trên là 35,58.
Câu 32:
Cho mẫu số liệu sau:
24; 16; 12; 5; 9; 3.
Tìm độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần trăm).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Số trung bình của mẫu số liệu trên là:
¯x=24+16+12+5+9+36=11,5.
Công thức tính phương sai của một mẫu số liệu là:
S2 = \(\frac{1}{n}\left[ {{{\left( {{x_1} - \overline x } \right)}^2} + {{\left( {{x_2} - \overline x } \right)}^2} + ... + {{\left( {{x_n} - \overline x } \right)}^2}} \right]\)
Thay số ta có:
S2 = 16[(24 – 11,5)2 + (16 – 11,5)2 + (12 – 11,5)2 + (5 – 11,5)2 + (9 – 11,5)2 + (3 – 11,5)2] ≈ 49,58.
Do đó phương sai của mẫu số liệu trên là 49,58.
Độ lệch chuẩn của mẫu số liệu trên là S = √S2= √49,58 ≈ 7,04.
Câu 33:
Trong mặt phẳng tọa độ Oxy, cho điểm A(1; 2) và B(3; – 1). Độ dài vectơ →AB là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: →AB=(2;−3), suy ra |→AB|=√22+(−3)2=√13.
Câu 34:
Trong mặt phẳng tọa độ, cho →u=3→i−5→j. Khi đó tọa độ của vectơ →u là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: →u=3→i−5→j=3→i+(−5)→j. Khi đó tọa độ của vectơ →u là →u=(3;−5).
Câu 35:
Góc giữa vectơ →a=(1;−1) và vectơ →b=(−2;0) có số đo bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: →a.→b=1.(−2)+(−1).0=−2, |→a|=√12+(−1)2=√2,|→b|=√(−2)2+02=2.
⇒cos(→a.→b)=→a.→b|→a|.|→b|=−22√2=−1√2⇒(→a.→b)=135∘.
Câu 36:
Để làm đường điện dây cao thế ở Hà Giang từ vị trí bản A đến bản B, người ta phải tránh một ngọn núi nên người ta phải nối thẳng đường dây từ bản A đến bản C dài 12 km rồi nối từ bản C đến bản B dài 8 km. Qua đo đạc người ta xác định được ^ABC=65∘. Hỏi so với việc nối thẳng từ bản A đến bản B, người ta tốn thêm bao nhiêu tiền, biết mỗi km dây có giá 150 000 đồng.
 Xem đáp án
Xem đáp án
Ta mô phỏng bài toán như hình vẽ sau:
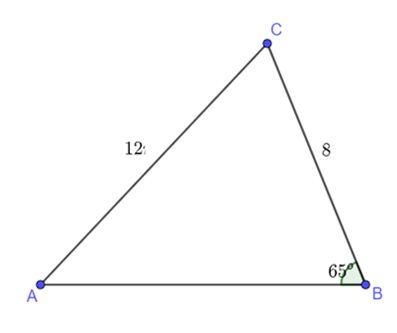
Áp dụng định lí côsin ta có:
AC2=AB2+BC2−2.AB.BC.cos^ABC
⇔144=AB2+64−16.AB.cos65∘
⇔AB2−16.AB.cos65o−80=0⇔[AB≈13AB≈−6,18(L)
Do đó: AB = 13 km.
Ta có: AC + BC – AB = 12 + 8 – 13 = 7 (km)
Vậy số tiền phải tốn thêm 7 . 150 000 = 1 050 000 (đồng).
Câu 37:
 Xem đáp án
Xem đáp án
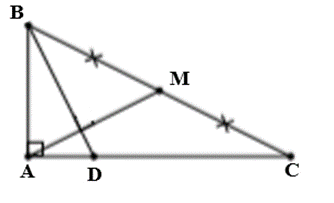
Xét tam giác ABC vuông tại A
Có: AB⊥AC ⇔ →AB.→AC=0 ⇔ →AB.→AD=0 vì D thuộc AC
Vì M là trung điểm của BC nên ta có: →AB+→AC=2→AM
Lại có: →BD=→AD−→AB (quy tắc ba điểm)
Khi đó ta có 2→AM.→BD=(→AB+→AC)(→AD−→AB)
=→AB.→AD−→AB2+→AC.→AD−→AC.→AB
=0−AB2+AC.AD.cos0∘−0
=−a2+2a.a2=0.
Vậy →AM.→BD=0⇔→AM⊥→BD⇔AM⊥BD (đcpcm).
Câu 38:
Cho mẫu số liệu sau đây:
2; 5; 1; 2; 8; 5; 45; 3.
Tìm giá trị ngoại lệ của mẫu số liệu trên?
 Xem đáp án
Xem đáp án
Sắp xếp mẫu số liệu trên theo thứ tự không giảm ta có:
1; 2; 2; 3; 5; 5; 8; 45.
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 1; 2; 2; 3.
Do đó Q1 = 2+22=2.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 5; 5; 8; 45.
Do đó Q3 = 5+82=6,5.
Khoảng tứ phân vị của mẫu : ∆Q = Q3 – Q1 = 6,5 – 2 = 4,5.
Ta có:
+ Q3 + 1,5∆Q = 6,5 + 1,5.4,5 = 13,25
+ Q1 – 1,5∆Q = 2 – 1,5.4,5 = – 4,75
Vì 45 > Q3 + 1,5∆Q nên 45 là giá trị ngoại lệ của mẫu số liệu trên.
